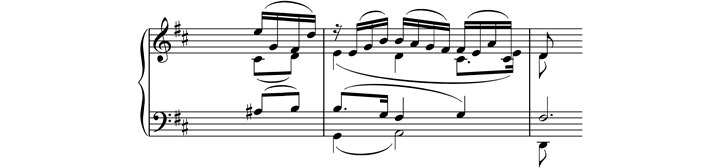Mozart, Ravel, die imperfizierte Kadenz und die perfekte Melodie

Das Modell Mozart

In Konzertführern und Biographien wird berichtet, Maurice Ravel habe den Mittelsatz seines Klavierkonzertes G-Dur (komponiert 1929–31) nach dem Modell des Larghetto aus Mozarts Klarinettenquintett A-Dur KV 581 geschaffen.[1] Die äußere Form, die als ternäres A-B-A mit Codetta (Ravel kürzt die Reprise und versieht sie mit variierter Begleitung) ein denkbar allgemein gehaltenes Formmodell darstellt, kann damit kaum gemeint sein. Diesem folgen ungezählte langsame Sätze der klassischen Epoche und der hieran anknüpfenden Neoklassik, der man Ravels Konzert wohl zurechnen darf. Komponisten erzählen mitunter viel, und häufig führen ihre Anmerkungen auf (zum Teil bewusst ausgelegte) falsche Fährten. Ein Vergleich auf interpunktischer Ebene ergibt jedenfalls beträchtliche Unterschiede in der Bauweise beider Sätze:

Mozarts A-Teil umfasst 30 Takte (der letzte Takt ist verschränkt mit dem Beginn des Mittelteils) und macht damit ein gutes Drittel der Gesamtlänge von 85 Takten aus. Er ist in den ersten 20 Takten als erweiterte Periode[2] gebaut, die Takte 20–30 bilden eine weitestgehend regelmäßige, satzartige Kadenzerweiterung. Beide Abschnitte kadenzieren zur Tonika D-Dur mit analog konstruierter ii⁶-V-I-Kadenz.

Beispiel 1: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Kadenz T. 19f.

Beispiel 2: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Kadenz T. 29f.

Ravel räumt dem ersten Teil mehr Länge ein: 45 Takte (bis Studienziffer 2) stehen insgesamt 108 Takten gegenüber. Auch hier zerfällt der A-Teil in zwei Abschnitte, äußerlich markiert durch den späten Orchestereinsatz in Takt 34. Allerdings setzt Ravel nur eine deutliche Interpunktion: Am Ende erfolgt eine äolische Kadenz[3] mit picardischer Terz nach Dis (Grundtonart E-Dur!). Ab dem Orchestereinsatz Takt 34 wird zwar auf der Dominante eine Kadenz eingeleitet, eine harmonische Ausweichung mündet jedoch Takt 36 ›trugschlüssig‹ in die IV. Stufe A-Dur – rein melodisch betrachtet findet die langgestreckte Klavierkantilene hier auf der Terz gis¹ ein befriedigendes Ende. Diese Kantilene als erweiterte Periode im klassischen Sinne zu betrachten ergibt wenig Sinn, da die Melodie viel eher einem satzartig schweifenden ›romantischen Fortspinnungstypus‹[4] gehorcht.

Beispiel 3: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, Schema imperfizierte Kadenz T. 34ff.

Beispiel 4: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, Schema äolische Kadenz T. 43ff.

Ein zentraler Begriff aber verweist auf die Gemeinsamkeiten zwischen den beiden ansonsten unterschiedlichen Werken: der der Melodie. Beide Komponisten formen primär durch Melodie. Also lohnt sich ein genauerer Blick auf die eröffnenden Melodielinien der A-Teile, vom jeweils weiteren Verlauf sollen nur die wichtigsten Punkte in die vergleichende Analyse einfließen.

Melodielehre

Leider gibt es kein allgemein übliches und akzeptiertes Analysewerkzeug für Melodie. Gegenüber zahllosen Versuchen, Harmonie lehr- und analysierbar zu machen, muss man sich zu diesem Thema die Rosinen hauptsächlich aus Kontrapunktlehren herauspicken (am weitesten in Richtung einer Melodielehre geht sicherlich Ernst Kurth[5]) oder sein Glück mit der recht überschaubaren Zahl von Werken über Melodie versuchen. Leider verzichten die meisten dieser Bücher auf einen einheitsstiftenden Ansatz; sie ergehen sich in Einzelbetrachtungen verschiedener Stilistiken.[6] Oder sie betrachten Melodik von vornherein abhängig vom (harmonischen oder kontrapunktischen) Zusammenklang[7] oder gehen allein vom Thematisch-Motivischen aus.[8] Trotz der relativ geringen Zahl deutschsprachiger Melodielehren erstreckt sich das inhaltliche Spektrum der Arbeiten sehr weit: von Carl Dahlhaus und Lars Ulrich Abraham[9], die Melodielehre ausschließlich historisch betrachtend verstehen und Anwendbarkeit auf das aktuelle Komponieren verleugnen (trotzdem oder gerade deswegen mit der bis heute vielleicht detailliertesten und grundlegendsten Methodik aufwarten) bis hin zu einem Übungswerk von Alfred Koerppen[10] mit Kompositionsübungen für das Studium – die entstehenden abstrakten Linien wirken wie Fux’sche Cantus firmi in freitonalem Stil. Ob die mit diesen Übungen gesammelten Erfahrungen auf die Analyse oder Komposition übertragbar sind, bleibe dahingestellt.

Am wertvollsten scheint mir – neben dem Schenkerschen Ansatz in der Vermittlung Felix Salzers[11] – die Melodielehre Christoph Hohlfelds. Da sie umfassend bisher nur mündlich bzw. in Form von Arbeitsblättern[12] mitgeteilt wurde[13], sei sie hier in aller Kürze skizziert: Aus dem römischen Choral und seinen Melodiemodellen (etwa den Psalm- und Magnificattönen) leitet Hohlfeld melodische Prinzipien ab, die er auch in der Musik späterer Jahrhunderte wiederfindet.[14] Er geht dabei von der Atemkurve des Sängers aus und überträgt diese auf den Spannungsverlauf der Tonhöhen-Linie. Das Urmodell einer melodischen Linie folgt dem Atemverlauf mit Initiale, Ténor und Cadenz.[15] Zentrale Töne wie z.B. der Ténor wirken als Tonebenen, die eigene Felder ausbilden und in eine Verlaufskurve über ganze Abschnitte oder Stücke hinweg integriert sind. Die grundlegenden Felder um zentrale Ebenen sind durch die kleine Terz und die Quarte begrenzt, die von ihm so genannte ›erste und zweite Affinitätsgrenze‹.[16] Hohlfelds Theorie speist sich aus einem breiten Repertoire an theoretischen und musikalischen Quellen: Vom antiken griechischen Tondenken über den römischen Choral, die Vokalpolyphonie Palestrinas[17] und die zeitgenössische Musiktheorie bei Zarlino bis hin zu Bach und Beethoven sowie deren Ausstrahlung in spätere Zeiten vermag Hohlfeld eine überzeugende historische Linie zu zeichnen. Dass er die vorklassische Epoche als die Wurzel des abendländischen Musikdenkens begreift, unterscheidet seinen Ansatz grundlegend von dem Schenkers.[18]

Hier soll versucht werden, die Melodieanalyse allgemein zu halten und nur mit unmittelbar verständlichen Begriffen zu arbeiten. Meine Hypothesen zu den Gesetzmäßigkeiten des Melodiebaus (in denen sich Hohlfelds Theorie und eigene Überlegungen mischen) sollen in den Text einfließen und an anderer Stelle zur Diskussion gestellt werden.

Der Vordersatz

Betrachten wir zunächst den neuntaktigen Vordersatz Mozarts im Vergleich zu den eröffnenden 15 Takten bei Ravel.

Beispiel 5: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, T. 1–9, Reduktion

Beispiel 6: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, T. 1–15, schematisiert

Hier wie dort liegt ein Melodie-Bass-Satz vor. Auf die genaue Wiedergabe der Mittelstimmen wurde in der Reduktion verzichtet: Bei Mozart bilden die drei hohen Streicher eine innerlich bewegte Akkordfläche, die gelegentlich kontrapunktisch belebt wird (z.B. in Takt 4). Ravels Klaviersatz verwendet eine scheinbar simple nachschlagende ›Humptata-Begleitung‹, die im weiteren Verlauf eigenständige Linienverläufe erhält (insbesondere in den Takten 11ff.). Was zunächst nur der Partiturleser sehen kann: Die rhythmische Faktur des begleitenden 6/8 steht im Widerspruch zur angegebenen Taktart 3/4, der die Oberstimme folgt – dies aber eher äußerlich: Hören werden wir wohl eine synkopierende Oberstimme in Konfliktrhythmik zum gehörten 6/8-Metrum, einen Dauerschwebezustand (etwa in den Takten 2f.).

Beide Melodien interagieren in hohem Maße mit der zugrundeliegenden Harmonik und der Stimmführung der begleitenden Stimmen. Beide Male spielt zudem (wenngleich auf sehr unterschiedliche Weise) die rhythmisch-metrische Gestaltung eine wichtige Rolle.[19]

Blenden wir dennoch Harmonik und Metrik zunächst aus. Mozarts Melodie entfaltet sich innerhalb eines Heptachords, das als zwei im d² (als Synaphe) verbundene Tetrachorde begriffen werden kann. In der Theorie Christoph Hohlfelds besitzt das Tetrachord herausragende Bedeutung[20], und zwar von der griechischen Musiktheorie über die Vokalpolyphonie des 15. und 16. Jahrhunderts bis ins 20. Jahrhundert (z.B. bei Bartók). In seiner Melodielehre bildet die Quarte die vielleicht wichtigste, da im Allgemeinen weiteste Grenze des tenoralen Feldes (also des Tonraums um den zentralen Ton), die sogenannte ›zweite Affinitätsgrenze‹.[21] Bei Mozart sehen wir eine typische Integration von Harmonischem in Melodischem: Der Ténor ist Grundton, und die eröffnende Dreiklangsbrechung ist Konvention im klassisch-harmonischen Stil – durch Zugrundelegung einer Dreiklangsharmonik werden Tongrenzen leichter überwunden. Die Brechung wird aber auch linear sensibel gehandhabt: Der Quartsprung a¹-d² schafft genügend Energie für das Anlaufen der Linie, in der Abwärtsbewegung der Welle füllen cis² und h¹ die entstehende Lücke auf. Auch in der oberen Hälfte der Welle wurde eine Stufe ausgespart, das e². Mit diesem Ton beginnt die zweite Welle. Unabhängig von ihrer rhythmischen Gestalt stellen sich die Töne der beiden ersten Wellen als Sequenz dar:

Beispiel 7: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Sequenzstruktur T. 1–3, Tetrachorde

Sequenzen bilden eine wichtige Stütze des Melodienbaus. Die kognitive Forschung weist ihnen die einleuchtende Funktion zu, die Zahl der erinnerten Einzelereignisse im Kurzzeitgedächtnis zu erhöhen, indem statt lauter Einzeltönen Tonkomplexe erinnert werden. Mozarts höchst individuelle Verwendung dieses Mittels zeigt uns eine besondere Qualität seiner Melodie: wörtliche Wiederholungen finden nicht statt (etwa im Sinne einer Wiederholungs- oder Entwicklungsperiode). Selbst da, wo ein Rhythmus wiederkehrt, erscheint die Melodieführung variant. So kehrt der Rhythmus der Takte 3f. in den Takten 5f. in freier melodischer Umkehrung wieder; obendrein wird er durch die Tonwiederholung des h¹ anders artikuliert:

Beispiel 8: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Gegenüberstellung T. 3f. und 5f.

Takt 5 bildet auch einen sequenzartigen Bezug zu Takt 1, allerdings nur im Ambitus: Das Rahmenintervall der Sexte a¹-fis² wird in Takt 5 einen Ton höher aufgegriffen. Wurde das g² bisher nur als Spitzenton gestreift, bildet es nun den deutlichen Höhepunkt des Vordersatzes. Mit dem g² beginnt auch ein Quartzug, der erst am Ende der Melodie in Takt 20, nach einer ausführlichen Prolongation, ins d² mündet. Die Mittel der Ausgestaltung sind vielfältig und nur zum Teil melodischer Art. Die chromatische Anreicherung der Linie in Takt 6 steigert einerseits die melodische Spannung, bildet aber andererseits auch einen unmittelbaren Reflex auf die kontrapunktisch-harmonisch wirksame Abwärtschromatik der Mittelstimme in Takt 4.

Die Takte 7–9 stellen in gewisser Weise ein Paradox dar: Die Melodie füllt wellenartig und schrittweise die zuletzt entstandene Lücke zwischen dem Spitzenton g² und dem mittleren Ton d² auf. Rhythmisch liegt ein auskomponiertes Ritardando vor, und es scheint, als habe hier die innere Erweiterung des (neuntaktigen) Vordersatzes ihre Ursache.[22] Tatsächlich könnten wir die Notenwerte der Takte 7f. einfach halbieren und gelangten so zu einem befriedigenden, wenn auch unspektakulären Achttakter. Ausgerechnet in diesen beiden Takten aber finden die häufigsten Harmoniewechsel statt. Wir können nun nicht die harmonische Folge D⁷-T-D-T-S-D ebenfalls im Tempo verdoppeln – der Effekt wäre grotesk. Aus ›schenkerianischer‹ Sicht prolongieren die Takte 7 und 8 die IV. Stufe. Der Eintritt der V. Stufe (die im Verlauf der Prolongation auf nachrangiger Ebene des öfteren anklingt) wird endgültig in Takt 9 empfunden (mit dem kadenzierenden Quartsextakkord). Aber erst die rhythmische Formulierung, die ein Schenker-Graph nicht abbildet, gibt der Stelle ihren Zauber: während die Melodie gewissermaßen stehenbleibt, halten die schnellen, simplen Harmoniewechsel die Bewegung am Laufen – ein wunderbarer Effekt des »Verweile Augenblick!«. Beispiel 9 zeigt eine Schenkersche Reduktion und die idealtypische Version der zusammengefassten Takte 7 und 8:

Beispiel 9: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Schenkergraph T. 1–20, T. 7 und 8 zusammengefasst

.Für das Ravel-Beispiel erscheint eine isolierte Betrachtungsweise, die zunächst Harmonik und Rhythmik-Metrik ausblendet, ungleich angemessener. Wie oben schon bemerkt, handelt es sich bei der eröffnenden Melodie um einen Fortspinnungstypus, periodische Metrik fällt somit nicht stark ins Gewicht. Außerdem sorgt die zugrundegelegte Konfliktmetrik 3/4 gegen 6/8 für einen dem Hörer unbestimmbaren Schwebezustand.

Zunächst fallen Unterschiede zwischen den Stücken stärker auf als Gemeinsamkeiten (ab dem Nachsatz gibt es dann äußerliche Entsprechungen). Anders als bei Mozart hebt die Linie nicht mit einer tonikalen Dreiklangsbrechung an, sondern mit einer Umspielung der 3. Stufe[23] gis¹.[24] Nach dem Herabsenken zum Grundton erfolgt der erste Sprung – zur 5. Stufe. Diese wird ebenfalls umspielt, allerdings mit der Umkehrung der eröffnenden vier Töne (diese motivische Zelle wird in der Notengrafik mit α bezeichnet) und mit wesentlich schnelleren Notenwerten, was dieser Version fast den ornamentalen Charakter eines unteren Doppelschlages gibt. Die Figur kehrt auch in der Manier einer solchen Verzierung zur umspielten Note h¹ zurück.

Nach Hohlfeld stellt die kleine Terz die erste Affinitätsgrenze dar. Das Kleinterzfeld ist das engaffinitive Feld um den zentralen Ton: Die Halbtonschritte als leitende Töne (Sub- und Supersemitonium), die Ganztonschritte als neutrale (zurück oder in die Gegenrichtung führend), die kleine Terz als erster Sprung, einerseits dem zentralen Ton zugehörig, andererseits mit der Möglichkeit ausgestattet, zur weitaffinitiven Sekundärebene, der Quarte zu führen oder ein eigenes Feld auszubilden. In diatonisch-harmonischer Musik werden wir kaum ein symmetrisches Kleinterzfeld um einen zentralen Ton finden, »da ja das harmonische Prinzip auf der Ungleichheit der Distanzen zur Schließung von harmonischen größeren Einheiten beruht.«[25] Ist der zentrale Ton – wie hier – die 3. Stufe in Dur, wird die untere Terz zu einer großen. So weitet Ravel zunächst das Feld um das zentrale gis¹ mittels des oberen Leittons a¹ (in bittersüßer Dissonanz zur unbeirrt weiter erklingenden Tonika E-Dur), die Linie gelangt über das fis¹ zur unteren Affinitätsgrenze e¹ und schwingt sich zum oberen affinitiven h¹ auf. Dieses wird dann auf ähnliche Art ausgebaut wie der Anfangston.

Man könnte im Gebrauch der motivischen Zelle α eine erste Ähnlichkeit zur Mozartschen Linie sehen: Techniken des Sequenzierens werden verwendet, wörtliche Sequenzen hingegen durch Variantenbildung vermieden. Da dies aber ein allgemein übliches Mittel des Melodiebaus ist, fallen die Unterschiede wohl mehr ins Gewicht: bei Mozart ausschwingende Dreiklangsmelodik, die innerhalb von gut zwei Takten alle Töne der im Grundton verbundenen Tetrachorde berührt, bei Ravel vorsichtiges, stufenweises Erschließen des Ambitus, der symmetrisch um die Terz angeordnet wird. Folgerichtig muss der nächste neue Ton auch dis¹ lauten. Er wird jedoch erst mit der übernächsten Welle erreicht. Spätestens hier wird klar, dass diese Linie auf fortspinnungsartige Länge, Welle um Welle, angelegt ist und nicht auf klar gebaute Periodik.

Beispiel 10: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, Länge und Gestaltung der ›Wellen‹ T. 2–15

Gleichwohl deutet der Bau der vier Wellen Ravels persönliche Anverwandlung klassischer Periodik an: Welle 2 und 3 (Takte 6–11) stellen in gewisser Weise eine verlängernde Ausgestaltung der bisher erreichten Stufen 1–6 dar. Der Abschnitt wird von den Tönen h¹ und cis² eingerahmt, so dass Takt 12 mit Auftakt nahtlos an Takt 5 anschließen könnte. Denkt man sich die Verlängerung weg, so ergibt sich ein Achttakter – aber genau in dieser ›inneren Erweiterung‹ beginnt die Melodie zu blühen, wird der Ambitus in ausdrucksvoll kreisenden Bewegungen (crescendo zu Takt 11 und diminuendo zu Takt 12!) durchschritten.

Beispiel 11: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, Verklammerung T. 6–11, hypothetischer Achttakter

Dass Höhepunktbildung gerade in Erweiterungen der Satzbildungen erreicht wird, ist bei Mozart die Regel. Als Beispiele mögen zwei erweiterte Perioden aus Mozart-Klaviersonaten dienen: KV 282, II. Satz: Menuett, A-Teil; KV 283, I. Satz Takt 1–16.[26] Auch im Nachsatz aus KV 581 findet sich dafür ein typisches Beispiel.

Der Nachsatz

Beispiel 12: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, T. 10–20, Reduktion

Nach der prolongierenden Wirkung der Takte 7–9 kommt Mozarts Melodie vermittels eines Dominant-Sekundakkordes nun gewissermaßen ins Rollen: In Takt 10 tauchen das erste Mal Sechzehntel in Kette auf. Mit dieser neugewonnenen Energie wird in Takt 12 ein neuer Spitzenton erreicht, der nur in der äußeren Erweiterung in Takt 19 überboten wird. Dass es sich bei den Takten 17–20 um eine äußere Erweiterung des ansonsten achttaktigen Nachsatzes handelt, ist durch die elegante imperfizierte Kadenz in den verminderten Septakkord der Doppeldominante zu Takt 17 leicht nachvollziehbar. Dasselbe Kadenzmuster wird mit gesteigerter melodischer Wirkung in Takt 20 ›korrigiert‹, d.h. zur Tonika geführt.

Beispiel 13a: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, imperfizierte Kadenz T. 15ff.

Beispiel 13b: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Kadenz T. 19ff.

Was aber in den Erweiterungstakten passiert, ist von so großem Zauber, dass allein die Aufzählung der Ereignisse einen Eindruck der Originalität geben dürfte:

• der Trugschluss in den DDv;

• der ›Absturz‹ der Klarinettenlinie um zwei Oktaven, ein Klangereignis von großer Markiertheit, das zudem die sensibel aufgebaute Ambitussymmetrie gründlich stört;

• der chromatische Anstieg (nach dem Modell eines sekundweise steigenden Quintfalls) in Takt 18.;

• das Erreichen des Spitzentons h² in Takt 19, im Zuge der ersten Dreiklangsbrechung in Sechzehnteln.

So unvermittelt die Ereignisdichte der Takte 17–20 erscheinen könnte, so gut ist sie dennoch vorbereitet:

• Der Rhythmus kommt bereits in den Takten 10–16 mit Sechzehntelketten in Bewegung;

• Der chromatische Bass-Gang Fis-F-E (mit F als Terz der Moll-s) leitet in Takt 12f. eine kurzfristige Ausweichung nach A-Dur ein.

• Der Ton dis² (Takt 19) reflektiert bereits in Takt 12 als neue Symmetrieachse die Ambituserweiterung um den Ton a².[27]

• dis und f kreisen e ein, als die Mitte des Gesamtambitus der Takte 1–20 (a¹–h²);

Beispiel 14: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, Ambitussymmetrien

• Harmonische Angelpunkte sind die beiden dominantischen Sekundakkorde (Takt 10 zur T und Takt 14 zur S) in Ponte-Wendungen (kadenzielles Umkreisen der V. Stufe in den Takten 10–13 und der I. Stufe in den Takten 14–16).[28]

• Der Absturz der Klarinette in Takt 17 bringt eine oktavversetzte und chromatisierte Variante der drei letzten Stufen des Quartzuges, der die Takte 16–18 überspannt (siehe Beispiel 12).

Beispiel 15: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, T. 16–36, schematisiert

Im Nachsatz Ravels finden sich direkte Anleihen an das mozartsche Vorbild. Wie der Nachsatz des Klarinettenquintetts setzt der des Klavierkonzerts in Takt 16 mit einem Sekundakkord an, auch hier wird neue rhythmische Energie gewonnen: durch Einführung des punktierten Achtelrhythmus im Auftakt. Die Takte 16–18 durchschreiten den bereits erreichten Ambitus h–cis² noch einmal, aber in entscheidend anderer Form: Das untere Ende des Ambitus’ wird ausgebaut, indem die tiefste Note h lang und relativ betont erklingt; der Aufstieg erfolgt zum ersten Mal in treppchenartigen Wellenkräuselungen (Takt 17); die gesamte Welle von gut drei Takten umschließt einmal mehr das zentrale gis¹, das ausgespart, von beiden Seiten umspielt und schließlich den ganzen Takt 18 hindurch gehalten wird. Das Crescendo unterstützend, schlägt die linke Hand in Takt 17 zum ersten Mal Bass und Mittelstimmen gleichzeitig an.[29] Takt 18 ist mehrfach markiert durch die erste punktierte Halbe, das erste Vorzeichen his und die spannungsvolle Harmonie des Gis⁷ mit Vorhalt e-dis im Bass.[30] Besser vorbereitet kann die Einlösung der erwarteten Ambitussymmetrie gar nicht eintreten: Endlich in den Takten 19 und 21 erscheinen die Spitzentöne e² und dis², zwei abrollende Wellen anführend, die sich wieder sequenzähnlich zueinander verhalten, wiederum durchsetzt von verschiedenen Ausformulierungen der motivischen Zelle α, auf deren genaue Darstellung ab hier verzichtet werden kann.

Am klassischen Vorbild geschult werden die Spitzentöne jedoch jeweils auf leichter metrischer Position gebracht. Zusätzlich verwendet Ravel einen für ihn typischen Kunstgriff: Konventionell würde man den Spannungsakkord Takt 18 mit einem Crescendo und womöglich einem verbreiternden Rubato verbinden. Ravel bevorzugt die délicatesse eines Diminuendo und eines nachfolgenden Pianissimo auf den Spitzentönen, trotz oder gerade wegen des ausdrucksvollen Sextsprungs gis¹-e²-gis¹ – sehr typisch für diesen Komponisten.[31]

Auch die Takte 23–26 bilden einen Bezug zum Vorbild Mozart: Die Melodie der rechten Hand ›taucht‹ jetzt unter die Begleitung der linken (dynamisch das erste explizite Mezzoforte). Natürlich ist der Zusammenhang ein anderer als in den Takten 17f. des Mozart-Beispiels, und Ravel zieht ganz andere Konsequenzen daraus, aber die Geste ist zu stark verwandt, als dass sie zufällig sein könnte. Während des ›Abtauchens‹ werden zwei neue tiefste Töne erreicht: a und gis. Anders als Mozart Takt 17 nach dem Registerwechsel folgt Ravel nun weiter der sorgfältig etablierten Ambitussymmetrie: die Melodie schwingt sich zu ihrem absoluten Höhepunkt fis² in Takt 30 auf, diesmal betont und im Forte. Das die Symmetrie vervollständigende gis² bleibt aus und schafft Spielraum für die Fortspinnung ab Takt 36.[32] Wie schon gezeigt, greift auch Ravel zum Mittel der imperfizierten Kadenz, im Gegensatz zu Mozart erst am Ende der eröffnenden Melodie und verschränkt mit der Fortspinnung. Diese schafft jedoch mit den sich gegenseitig umschlingenden Melodien der verschiedenen Holzbläser wieder einen direkten Bezug zum Klarinettenquintett.

Die Fortspinnung

Beispiel 16: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, T. 20–24 (nur Melodiestimmen)

Beispiel 17: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, T. 35–45 (nur Melodiestimmen)

Ravels Klavierkantilene findet zwar, wie erwähnt, melodisch mit dem gis² Takt 36 einen befriedigenden Abschluss; dennoch bilden aber die mit der Penultima einsetzenden Holzbläserlinien eine logische, strukturell eingebettete Fortsetzung. Einiges spricht dafür, diese Einwürfe als ins oktavierende Register geklappte Linien zu sehen:

• die Wiederholung der Takte 32f. durch die Flöte in den Takten 35f. mit Auftakt,

• die Erweiterung des Ambitus bis zum ais in Takt 42 (damit die Symmetrieachse wieder nach oben verschiebend).

• Das in Takt 45 (als Finalis einer äolischen Kadenz) erreichte, ›entlegene‹ Dis-Dur (siehe Bsp. 4) kann gesehen werden als korrigierende Reaktion auf die verschobene Symmetrieachse. Ab Takt 45 nutzt Ravel diesen tonalen Zusammenprall für aparte ›bitonale‹ Mischungen zwischen ›Dis-Dur‹ bzw. melodischem cis-Moll (Klavier linke Hand und Orchester) und ›E-Dur‹ (Klavier rechte Hand). Dreh- und Angelpunkt ist der gemeinsame Ton gis (!), präsent als Ligatur in der Klarinette. . Gleichzeitig ist diese querständige bitonale Mischung in eine konventionelle Skala integrierbar: Die Konflikttöne h und a der rechten Hand sind Bestandteil des oben erwähnten melodischen cis-Molls.

Auch Mozart spielt mit der Kadenz, selbstverständlich nicht auf entfernten Stufen oder gar in bitonalen Zusammenhängen. Er verwendet in der Fortspinnung sogar eine sehr einfache Harmonik (größtenteils nur Hauptstufen), aber das Verhältnis der Kadenzen ist wieder sehr gut ausbalanciert. Beide Kadenzen (zu den Takten 27 und 30) sind auf unterschiedliche Weise imperfiziert und halten dadurch den musikalischen Fluss am Laufen: Takt 27 endet auf dem Sextakkord und wird in der Melodie sofort in Sechzehnteln überspielt, Takt 30 ist verschränkt mit dem Mittelteil und ändert die Harmonie auf Zählzeit zwei zum h-Moll-Sextakkord.

Beispiel 18: W.A. Mozart, Klarinettenquintett A-Dur KV 581, Larghetto, T. 24–31, Kadenzen in T. 27 und 30

Die überspielende Imperfizierung der Kadenz zu Takt 27 hat außerdem eine interpunktische Konsequenz: Die Fortspinnung gestaltet Mozart als Schlusssatz, in dem die Takte 27–30 als äußere Erweiterung fungieren. Damit kommt der Schlusssatz auf die insgesamt unregelmäßige Zahl von 11 Takten: viertaktiger Halbsatz (Takte 20–23), viertaktige Kadenz, verschränkt mit äußerer Erweiterung um vier Takte (Takte 24–30). Takt 30 ist – wie oben erwähnt – gleichzeitig der erste Takt des Mittelteiles.

Das Phänomen, dass ein überzähliger Takt zu Beginn (hier Takt 8) durch Verkürzung im Schlusssatz wieder eingespart wird, kann bei Mozart gelegentlich beobachtet werden – bekanntestes Beispiel ist der I. Satz der Sonata facile KV 545: Der einleitende, die Geradtaktigkeit ›störende‹ Takt 13 des Seitensatzes wird durch eine nur dreitaktige Schlussgruppe (Takte 26–28) ausgeglichen.

Der Mittelteil und die Reprise

Wie angekündigt können hier nicht die ganzen Sätze analysiert werden. Es soll aber auf Punkte hingewiesen werden, die untermauern, dass Ravel tatsächlich Mozarts Satz als Vorbild genommen hat.

Beide Mittelteile verwenden hauptsächlich Sequenzen mit schwebenden Harmonien und Läufen der melodieführenden Instrumente. Ravels bitonale Harmonien sind quasi eine moderne Übersetzung der – es gibt kein treffenderes Wort – schwebenden Vorhaltsketten Mozarts (Takte 34ff. und 45ff.). Die Sequenzen sind jeweils ausführlich gestaltete Quintfälle mit Zwischendominanten.

In beiden Fällen werden die Sequenzketten durch eine Mittelkadenz geteilt, die bei Mozart nach A-Dur geht (Takte 44f.), bei Ravel nach G-Dur (Takt 65, 1 Takt vor Studienziffer 5). Worin besteht nun die Ähnlichkeit – Mozarts Kadenz führt zu einer konventionellen Stufe, der Oberquinte, Ravels jedoch in eine Mediante? Die Stufen repräsentieren jeweils die Haupttonart des Gesamtwerkes. Im neueren Werk wird also die inzwischen zu konventionell gewordene Dominanttonart durch die frischere Mediantwirkung ersetzt, die trotzdem auf ähnliche Art in den gesamten Zyklus integriert ist.

Vor der ersten Sequenz gliedert Ravel zusätzlich durch eine weitere Kadenz nach D-Dur (Takt 57, 1 Takt vor Studienziffer 4), deren Bedeutung sich im Gesamtzusammenhang (siehe Beispiel 20) offenbaren wird.

Jeweils die zweite Sequenz führt zum dynamischen Höhepunkt des Satzes, ein A⁷ im Forte mit nachfolgender kleiner Solokadenz der Klarinette bei Mozart (Takt 49), das erwähnte gis-Moll über G im Fortissimo bei Ravel (3 Takte vor Studienziffer 6).

Die Reprisen fallen etwas unterschiedlicher aus, was wohl der Form geschuldet ist. Im Kammermusikwerk erfolgt die Reprise wörtlich und mündet in eine kleine Coda über einem Tonika-Orgelpunkt, im konzertanten Satz umspielt das Soloinstrument die Anfangsmelodie in Zweiunddreißigsteln. Die Kürzung der Melodie um 10 Takte hat wie erwähnt eine Bedeutung für die Ambitussymmetrien[33]; darüber hinaus hat sie natürlich eine dramaturgisch straffende Funktion. Einen Trumpf hat Ravel allerdings noch im Ärmel: Er verändert und verkürzt in der Reprise die Fortspinnung und kadenziert an der Parallelstelle zu Takt 36 imperfizierend nach Cis-Dur.[34]

Beispiel 19: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, T. 96f.

Von dort baut er fast einen traditionellen Quintfall (sozusagen einen ›Turnaround‹) zurück zur Tonika. Als kleine Referenz an die erste Harmoniefortschreitung E-Dur/gis-Moll verändert Ravel die erwartete Dominantharmonie H-Dur jedoch zu gis-Moll, das hier mit der Durchgangsharmonie eines fis-Moll-Septakkordes plagalschlussartig in die Tonika geführt wird. Über dieser lässt er – wie Mozart – den Satz über einem Orgelpunkt verklingen.

Übergeordnet ergeben die Kadenzen (imperfizierte und vollständige sowie Halbschlüsse) des Satzes eine logische Folge, die großflächig die Bassführung der Anfangsmelodie widerspiegelt: beruht doch die Harmonik des Satzes überwiegend auf stufenweise meist abwärts gehenden Bässen (wie auch die meisten Bewegungen der nachschlagenden Mittelstimmen aus Stufengängen bestehen), gelegentlich durch Quintfälle gegliedert. Hier ergeben sich zwei ineinander verschachtelte Stimmzüge, die in der Notengrafik herausgestellt sind:

Beispiel 20: Maurice Ravel, Klavierkonzert G-Dur, II. Satz, wichtigste Stufen des Satzes

Zusammenfassung

Auch wenn die Unterschiede deutlich ins Auge fallen, darf doch angenommen werden, dass Ravel seine Art der Melodie- und Formbildung am mozartschen Beispiel geschult hat. Dass die Dichte der äußerlichen Entsprechungen innerhalb der Eröffnungsmelodie zunimmt (Sekundakkord, Abtauchen, Imperfizierung), könnte eine ganz einfache Erklärung haben: Der Beginn ist typisch Ravelsche Melodie-Erfindung (man beachte die melodische Ähnlichkeit zum ›Boléro‹, in gewisser Weise auch zu den ersten beiden Sätzen der Sonatine für Klavier und zum Beginn des Klaviertrios), die weitere Entwicklung ist auf das Mozart-Vorbild zugebaut (was die Originalität nicht mindert!). Neben den vielen Entsprechungen im Detail sind es vor allen Dingen das Gestische und das Atmosphärische, die beide Stücke in Nähe zueinander rücken. Um es am Ende dieser Analyse einmal blumig auszudrücken: Beiden Komponisten gelingt es durch Finessen der Melodik und Harmonik, den aufmerksamen Hörer von einer Verzückung in die andere fallen zu lassen. Unter der glatten Oberfläche von klassizistischer Form und perfekter Melodie liegen unauslotbare Tiefen. Wir wissen, dass diese Tiefen bei beiden Komponisten etwas Tragisches oder Katastrophisches haben können[35]; dies können wir bei den beiden betrachteten Werke nicht erblicken. Aber beide drücken ihre bei genauerer Betrachtung durchaus dunkel-erotische Gefühlswelt durch (geradezu ungenierte) musikalische Schönheit aus, ohne jemals ins Schwüle abzurutschen. Bändigung erfolgt bei beiden durch die strenge, symmetrische Form und feinste Abstufungen (hier z.B. repräsentiert durch die sensibel eingesetzten imperfizierten Kadenzen und die Eleganz der rhythmisch-melodischen Diktion).

Dass Mozart ein Melodiker ersten Ranges ist, daran bestand wohl niemals irgendein Zweifel. An dieser Stelle sei heftig dafür plädiert, auch in Ravel einen großen Melodiker zu erkennen – vielleicht den größten der ersten Hälfte des 20. Jahrhunderts. Nach seinen impressionistischen Anfängen, die sich naturgemäß mehr um Kategorien des Klangs und der neuen Formdiktion gekümmert haben, wandelte er sich zu einem Neoklassiker, der die Gesetze der mozartschen Melodiebildung lernte, erfolgreich in seine Gegenwart transportierte und sich anverwandelte. Als Beispiele seien seine späteren Kammermusikwerke angeführt: die Duosonate für Violine und Cello (1920–22), die Violinsonate (1923–27); Ansätze zu einem melodisch-kontrapunktischen Stil finden sich bei ihm freilich bereits früher, auch – wenngleich auf andere Art – in seinen vokalen und orchestralen Werken.

Um auf sein populärstes Werk hinzuweisen: Durch was sonst als eine perfekte Melodie kann ein Werk bestehen, das nur aus eben dieser (und einer Variante) besteht?