Some of the most celebrated controversies engendered by Glenn Gould’s interpretations involve unconventional tempo choices. Gould often justified these with an appeal to the concept of large-scale structure. The slow pace of his 1962 performance of Brahms’s D minor piano concerto with Leonard Bernstein and the New York Philharmonic has been exaggerated – at the time primarily by Harold Schonberg’s review in the New York Times, and later by Bernstein himself.[1] Twenty-first-century performances regularly exceed Gould/Bernstein’s fifty-three minutes. In his essay “N’aimez-vous pas Brahms?” Gould described his goal of repairing the work’s “architectural deficiencies.”[2] Gould’s performance of the first movement of Mozart’s Sonata K. 331 – with its extremely slow opening and gradual increases of speed for each successive variation – has become an emblem of eccentricity in the literature. Kevin Bazzana’s analysis forms the climax of a section describing Gould’s relationship to the score.[3] Peter Martens begins his discussion of Gould’s tempo choices and their relationship to large-scale structure with it.[4]

Gould often looked for ways to increase his listeners’ sense of unity and coherence across multiple movements of a work; tempo choice was one of his most important tools. The 1962 Brahms concerto performance with Bernstein features a continuous pulse rate between the movements. Gould’s recordings from the 1970s – particularly dance suites by Bach – show his increasing interest in proportional tempi. The culmination of this line of development is his 1981 recording of the “Goldberg Variations.” In Bruno Monsaingeon’s film The Goldberg Variations (1981), Gould claims that he was motivated to revisit the work that made him famous by a desire to craft a large-scale structure. The 1955 recording that thrust the twenty-three-year-old pianist to the height of stardom sounded like “thirty very interesting but somewhat independent-minded pieces going their own way.”[5]

For promotional purposes and to justify his new interpretation, Gould recorded a scripted interview with music critic Tim Page about the new “Goldberg” recording. The discussion dwells mainly on tempo choices and the proportionality of pulse rates, what Gould referred to as a “constant rhythmic reference point.”[6] In the detailed discussion of variations 16–18 Gould describes proportionality in terms not of what happens at the joints between sections or movements, but of the initial tempi; he sings the beginning of a section and takes that tempo to stand for the prevailing tempo. This is an architectural view of tempo relationships. Sections or movements have the solidity of building blocks; expressive tempo modifications are dismissed as surface features that do not change the prevailing tempo. The complete edifice, or well-structured performance, relies on the proportional fitting together of these blocks.

Viewed in this architectural way, any single movement can be instantly compared with any other and its fit judged accordingly. Tempo tables that assign a single metronome marking to a section or movement are the most common realization of an architectural approach to timing in performance, akin to charts that show motivic resemblances between non-adjacent material. Daniel Leech-Wilkinson has argued that theorists should re-focus their attention, away from large-scale form which psychological research suggests may not be audible, towards the moment-to-moment perception of the musical surface.[7] Despite the architectural orientation of Gould’s rhetoric, the much-admired structural coherence of his 1981 Goldberg recording appears to be based more on moment-to-moment processes than architectural relationships.

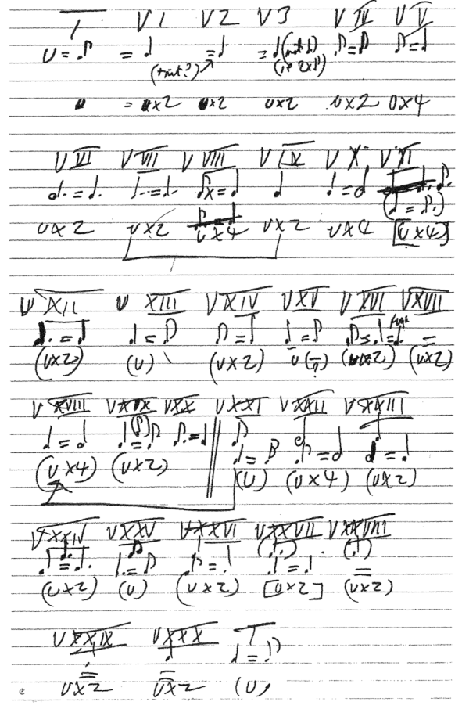
Figure 1: Notebook page detailing a tempo scheme for the 1981 “Goldberg Variations” recording
(Estate of Glenn Gould, dated 1979, reproduced in Bazzana 2004, 454)

Figure 1 is a page from one of Gould’s notebooks that details a tempo plan for the “Goldberg Variations.” Gould’s “u” represents an “ur-tempo,” in this case the eighth-note pulse of the Aria (capital “T” for “theme”). “U” and its multiples, the lowest of the three entries that describe each variation in the table, indicate the speed of eighth notes, not the tactus. For example, there is no “u” tempo that could reasonably accommodate an eighth-note pulse for the Aria and a “u x 4” mark for quarter notes in variation 5. Gould’s actual tempo in the 1981 recording starts at about  = 67.2 beats per minute (bpm) in the Aria, suggesting a tempo of  = 268.8 for variation 5. Even Gould’s slower tempo in the Aria da Capo (55.8 bpm) would imply an impossibly fast tempo of  = 223.2 for Variation 5. Gould’s Arias in 1981 and his 1955 version of variation 5 (174 bpm) are examples of his well-known penchant for extreme tempi; they may even be at the limits of possibility. Gould’s table determines the tempo of the eighth notes as a multiple – one, two or four – of the opening movement’s eighth notes in every variation except variations 11, 20, and the fugato section of variation 16. Note the double bar before variation 21: this most likely is a repercussion of variation 20’s tempo which is not a u-multiple.

The note values in Gould’s table represent rhythmic correspondences between movements. Starting in variation 21, the note value receiving the beat appears above the rhythmic correspondences and u-multiples. These rhythmic correspondences might be possible, but they are far removed from Gould’s actual practice. For example, the table suggests that variations 26 through 30 should all be played in the same tempo, though Gould’s actual tempi in the 1981 recording range from 73.1 to 111.8 bpm.

Gould’s tempo table shows a strong orientation toward architecture rather than process. His insistence that the eighth-note pulse of the Aria be present in nearly every variation as an eighth, quarter or half note – i.e., u, u x 2, or u x 4 – severely limits his choices of tempi. The scheme allows no tempo modification, though Gould seems to acknowledge this problem by writing “(+rit?)” after variation 1. For the ur-tempo to match, a variation’s final slowing must not influence the tempo of the next variation. Thus the rhythmic correspondences, though they seem to acknowledge that rhythmic continuity will be perceived at the joints between variations, actually must describe relationships among the prevailing or initial tempi of neighboring variations. The ur-tempo idea is a powerful constraint. It implies that memory for tempo, rather than continuity at the joints, is of primary importance. The problems inherent in the notation of this table show how Gould’s theoretical ideas about tempo, and particularly proportional tempo, diverge from the practice of music making.

A comment in the interview with Tim Page suggests how Gould’s process may have evolved from the table:

I have come to feel over the years that a musical work should have one pulse rate, one constant rhythmic reference point. […] I would never argue in favor of an inflexible musical pulse, you know, that just destroys any music. But you can take a basic pulse and divide it or multiply it, not necessarily on a scale of two, four, eight, sixteen, thirty-two, but often with far less obvious divisions, and make the result of those divisions or multiplications act as a subsidiary pulse for a particular movement or section of a movement.[8]

Gould’s attachment to powers of two, as seen in his tempo table, has weakened, but his architectural rhetoric has persisted. The “constant rhythmic reference point” clearly refers to the relationship of non-adjacent sections of music. In the interview he also admits the utility of tempo modifications: “If you have an accelerando, for example, you simply use the accelerando as a transition between two aspects of the same basic pulse.”[9] A tempo which does not show a power-of-two relationship with the reference tempo is justified not by local conditions – that is, the process of tempo modification that effects the change – but by its proportional relationship with the ur-tempo.

In the brief interview with Bruno Monsaingeon that prefaces the film version of his 1981 interpretation of the “Goldberg Variations,” Gould says: “Substituting for the fact that Bach has absolutely no melodic design that is continuous but rather a bass, [or a] harmonic design that is continuous, there would be at least a rhythmic design that was continuous and a sense of pulse that went through it.”[10] For Gould, a tempo plan might provide a sense of unity and structure in performance akin to what Bach could have created through motivic organicism. Note that Gould does not distinguish between structure perceived in performance and compositional structure embedded in the score. Gould avoids any description of structure as temporally emergent in performance, favoring an architectural point of view. Even when he discusses tempo, Gould privileges the idea of a unified whole and suggests a visual metaphor through his hand gestures, rather than describing the moment-to-moment decisions and processes of performance. Instead of the Aria being a reference point for melodic or motivic material, it is a reference point for tempo.

Bazzana’s Glenn Gould: The Performer in the Work is largely devoted to showing how Gould makes his analytical insights – score-based, usually focused on spatialized or architectural ideas such as motivic similarity – explicit through his interpretations.[11] Gould’s ability to project large-scale structure has been praised by many critics. Bazzana describes this ability as “intuitive,” partly because in 1997 the causes and effects of temporally-emergent large-scale structure in performance had not been adequately theorized.[12] Despite significant progress over the last twenty years, the question of the relationship between performance decisions and the perception of large-scale structure remains difficult. For example, Adam Behan demonstrates that pianists’ interpretations can call into question even supposedly straightforward score-based structures like the ABA form of Brahms’s op. 119 no. 2.[13]

Gould seems to know that the power of tempo to create long-range coherence depends on process rather than architecture. In the Tim Page interview – and it must be emphasized that this is a scripted radio play, not an interview in which questions might come as a surprise – Gould acknowledges that, in his 1981 recording, the tempo of the Aria da capo is noticeably slower than the tempo of the Aria. Intellectually, nothing could be more disastrous for a tempo plan founded on the idea of the Aria as a rhythmical reference point than an obvious discrepancy between the tempi of the Aria and the Aria da capo at the end of the cycle. The fact that neither Gould nor any of his commentators were bothered by this shows how the perception of coherence between movements through tempo choice does not depend on long-range memory but on moment-to-moment developments. The logical inconsistency of Gould’s comments shows how statements by performers cannot be taken at face value. Certain commonplaces of how we talk about music – notably, the idea that a single metronome number can describe a movement’s tempo – mediated Gould’s verbal description of his process.

In his review of the literature on proportional tempo likely to have been known to Gould, Bazzana states “it is difficult to assess to what degree he was influenced by specific writings or performers.”[14] Gould was aware of Arnold Dolmetsch’s 1915 The Interpretation of the Music of the Seventeenth and Eighteenth Centuries.[15] He wrote a review of Erwin Bodky’s 1960 The Interpretation of Bach’s Keyboard Works[16] without mentioning Bodky’s ideas about tempo. Through Bodky, he may have been familiar with the concept of tempo ordinario. Bodky groups Bach’s pieces into five speeds, suggesting mostly low-order proportional relationships.[17] However, Gould’s interest in proportional tempo was based not on historical authenticity, but on his belief that unified pulse rates enhanced his and his listeners’ perception of large-scale structure. Though Gould’s tempo table and comments in the Page interview suggest sympathy with the proportional theories of Walter Gerstenberg and Ulrich Siegele, there is no indication that he was aware of either theorist.[18] Nevertheless, Gould’s rhetoric is locked into the assumptions that underpin tempo tables like those found in Walter Schenkman’s, Nicholas Hopkins’s, and Siegele’s work.[19] These tables typically indicate initial or basic tempi and ignore transitions, implying that listeners perceive proportionality based on relationships between non-adjacent passages of music.

The architectural view of tempo in Gould’s rhetoric contrasts with his process of execution. Using a metronome is the most practical way to create a rhythmical reference point, but Gould’s letters suggest he did not own one.[20] Gould’s tempo table implies that the Aria serves as a reference. However, to make the 1981 Goldberg recording, Gould did not refer to a metronome, or the tempo of the Aria before starting each variation. Rather, he listened to the second half of the preceding movement, sometimes even playing along with the recorded sound; after the end of each variation, he would mark the entry of the subsequent variation by playing a few bars that would not be used in the final product.[21] Thus his tempo choices were not architectural, but processual; Gould’s specific tempi for each movement were derived from a continuous, embodied process.[22] Gould’s tendency to create subtle but large-scale tempo shapes across entire variations (to be demonstrated later in this article) amplifies the difference between this process and the use of a reference to determine tempi.

Recent research on Gould highlights the tension between Gould’s often abstract and polemical rhetoric and the more conventional aspects of his actual practice. Luk Vaes interrogates the relationship between Gould’s comments about using tempo to create increased structural coherence and his recorded performance of Brahms’s first piano concerto.[23] Garreth P. Broesche shows how Gould’s working process in the recording studio was less radical than his verbal descriptions of it.[24]

The present study will present an analysis of Gould’s tempo in the 1981 recording of the “Goldberg Variations,” particularly focusing on the macro-level strategies he employs to create large-scale continuity and structure. Using Sonic Visualiser to quantify the rhythm helps clarify Gould’s often subtle manipulations. The wealth of commentary on Gould’s performance style, and this recording in particular, creates a rich dialogue between listeners’ perceptions and empirical data. Similarly, I will examine the relationship between the literature on proportional tempo and Gould’s practice of it. As Nicholas Cook argues, performance “is to a very large extent an art of transitioning – in other words, it is oriented to precisely the horizontal dimension of music that the spatialised, hierarchical models of theorist’s analysis de-emphasize.”[25] Gould’s processual approach to proportional tempo calls some of the prevailing theoretical assumptions into question. More importantly, Gould’s timing strategies show how performers’ decisions relate to listeners’ perception of large-scale form.

Previous Research

The distinction between an architectural and a processual tempo plan – that is, one that refers to non-adjacent music and one that privileges local continuity – is latent in Bazzana’s analyses. About Gould’s recordings of Beethoven’s Sonatas op. 26 from 1979 and op. 27, no. 1 from 1981, he states: “Gould apparently sought rhythmic cross-references and large-scale rhythmic order through proportional tempos – including (unusually for him) relationships between opening tempos of some movements.”[26] Thus Bazzana acknowledges that Gould rarely chose tempi in order to create relationships between non-adjacent passages. In his analysis of the 1981 “Goldberg” recording, Bazzana argues that continuity is created mainly by careful calibration of timing at the joints between movements, rather than by proportional relationships of prevailing tempi. Further, he states that though “one can find some truly ‘arithmetic correspondences’ [of the sort Gould described in the Monsaingeon interview] in the final performance, those which can be considered meaningful are relatively few,” and that “exaggerating the mathematical nature of his tempo relationships, especially in this performance, is quite common in the Gould literature.”[27] Bazzana is careful not to overstate the limited empirical evidence for an architectural tempo plan.

Yet he avoids criticizing Gould’s architectural rhetoric. Though he carefully and correctly describes the tempo continuity arising from the sequential progress of the variations in his detailed analysis, Bazzana promotes the idea of the Aria’s tempo as a reference point in a more theoretical section. In the liner notes to his earlier Goldberg recording, Gould describes Bach’s structure as circular because the Aria’s “recurrent passacaille [i.e., ground bass] supplies the concentric focus for the orbit” of the variations.[28] In reference to the 1981 recording, Bazzana elaborates: “Gould underscores the circular effect audibly by applying throughout the principle of proportional tempo relationships from variation to variation, suggesting the continuing presence of the opening Aria, at some level, throughout the work.”[29] Under the heading “Performing the work as Gestalt,” Bazzana argues that Gould’s attempts to create large-scale structure often appeared “to the listener as an immediately palpable shape – as a linear progression, arch, double arch, circle” and that this sort of reification of music’s temporally unfolding processes was one of Gould’s goals as a performer and analyst.[30] As Bazzana points out, this rhetoric is infused with modernist ideals. Gould’s well-known admiration for Arnold Schoenberg influenced the way he thought, talked, and wrote about musical structure; in order to participate in that high-minded discussion, Gould may have felt he had to adopt an architectural point of view.

The other detailed study of tempo in Gould’s 1981 “Goldberg” recording is by Nicholas Hopkins, who describes Gould’s tempo plan in terms of rhythmic continuity and proportional tempo. Rhythmic continuity refers to the continuousness of the local pulse across the breaks between movements. Proportional tempo refers to the relationship of initial or prevailing tempi. Taking his cue from Gould’s comment in the interview with Page about a “subsidiary pulse” (quoted above), Hopkins identifies an “ur-tempo” and two subsidiary tempi – 60 bpm for the ur-tempo, 72 and 80 bpm for the subsidiary tempi. He states: “all tempo marking in this recording […] can be derived from arithmetical operations on one of these three values.”[31] The arithmetical operations he admits are multiplication by one-and-a-half and two. He describes tempi from 54 to 66 bpm as closely related to the ur-tempo of 60 bpm, suggesting a tolerance of 10% deviation from the expected value.[32] These definitions of proportionality, however, are not rigorous enough; by these rules every tempo between 54 and 264 bpm is closely related to either the ur-tempo or one of the subsidiary tempi.

In Hopkins’s score, a transcription of Gould’s 1981 performance, every joint between movements is marked with a correspondence of note values; for example, the final eighth note of the Aria equals the initial dotted half of variation 1. Many of these correspondences do not match my tempo data. Gould’s description of his process in the interview with Page may have led Hopkins to believe that the tempo of every movement is proportional to the preceding movement. However, Gould barely touches on his process of fashioning transitions with rhythmic continuity; the idea that every joint between variations features some kind of equivalence of note values is Hopkins’s own invention. I view Hopkins’s rhythmic correspondences as an attempt to quantify the powerful sense of continuity created by Gould’s transitions using common note values. The fact that they differ from objective measurement indicates not a lack of listening skills but the limited ability of notation to capture the nuance of performance. Not only does conventional notation fail to convey the emotional moment-to-moment trajectory of the music, a concept well-established in performance studies, it also does not capture the generators of listeners’ perception of large-scale structure.

Peter Martens tested listeners’ impressions of continuity in Gould’s performances in an experiment that compared responses to tactus in the 1955 and 1981 recordings of the “Goldberg Variations.” Listeners’ tapping responses were more diverse across the transitions in the 1955 recording, suggesting that the 1981 recording exerts greater control over the perceived pulse rate between movements.[33] Martens avoids the trap set by Gould’s architectural rhetoric; his article offers empirical support for the idea that Gould’s timing strategies create structural coherence, especially at the transitions.

Several articles by Christian Utz seek to induce architectural schema from the timing details of individual performances.[34] While these analyses take performances rather than scores as their point of departure, they are architecturally oriented. Utz focuses on how performers’ decisions about basic tempi in multi-movement works imply a macro-level interpretation of structure. He distinguishes between “spatialized,” “transformative,” and “presentist” time.[35] Spatialized and transformative time correspond to my terms architectural and processual. Presentist time refers to the experience of meaningful musical moments whose diachronic position is undermined by discontinuities, as theorized in Karlheinz Stockhausen’s concept of moment form. Utz cites Gould’s extreme contrasts of tempi as memorable discontinuities that contribute to the listener’s architectural understanding of the performance. My analysis will show how Gould’s precise shaping of transitions creates a processual connection, even at those moments of greatest discontinuity.

The theoretical literature on proportional tempo displays a strong emphasis on architecture. David Epstein makes both historical and biological arguments for proportional tempi as a “preferred way, in terms of coherence and unity,” of making music.[36] His historical arguments are predicated on the notion that a section of music has a prevailing tempo, a seemingly uncontroversial assumption that analyses of Gould’s performances call into question. For Epstein, tempo modifications will “create dissynchrony across temporal modes,” but will eventually “return into phase.”[37] Final ritardandi and the length of silences between movements, both critical issues for Gould, are not addressed.[38]

With his focus on the periodicity of neurological systems, Epstein investigates a different question than Martens or Gould. As described above, Gould listened to the end of the previous variation to set the tempo of each movement; his goal was to create a connection between movements, maintaining listeners’ focus in order to unify their impression of the macro-structure. For Epstein, proportional tempo is felt from the beginning to the end of a multi-movement work, as local beats continue at some rhythmic level the pulse of the previous section. He uses Gould’s architectural comments in the interview with Page to support his argument for proportional tempo’s preferred status, but he does not evaluate the recording empirically.[39]

Epstein’s definition of proportional tempo mostly coincides with Gould’s description of his process in the interviews with Page and Monsaingeon. For a proportional relationship to be perceptible, Epstein contends that it must reflect the simple, whole-number ratios 1:1, 1:2, 2:3, 3:4 or their inversions; his reason for limiting the proportions is that “proportionally related tempos involve phase synchrony,” and in the case of “higher-number ratios, this time span will exceed the fundamental time frame within which […] the nervous system cognitively processes basic temporal units.”[40] In the Page interview the most complicated ratio Gould describes is 2:3. Not intending a full explanation of his process, he gives few examples. Gould’s tempo chart shows only power-of-two relationships. When he comments in the Monsaingeon film that he sought a “tempo relationship, I don’t want to say just exactly 2, 4, 8, 16, 32, that kind of correspondence” he implies that the proportions 1:1 and 1:2 are more clearly audible than 2:3 and 3:4.[41] My analysis suggests that in at least one case Gould actively intended a proportion of 3:4 to be audible.

Studies of proportional tempo in the “Goldberg Variations” based in historical musicology offer some support for the architectural principles of Gould’s approach. Siegele argues that Bach conceived the movements of the “Goldberg Variations” as fixed in duration. Each half – the Aria plus variations 1–15, and variations 16–30 plus the Aria da capo – should take forty-five minutes to perform; the time signature and figuration of each movement imply a tempo which is then converted into a duration.[42] These tempi are related proportionally, following a system derived from Michael Praetorius and Lorenz Christoph Mizler.[43] Though Siegele’s theory that precise tempi indications are encoded in the score completely circumscribes the tempo decisions of individual performers, Utz points out that except for a few variations (3, 13, 18), this scheme is remarkably consistent with the tempi of a range of performers across the work’s recorded history.[44]

Siegele’s theory does not touch on the issue critical for Gould’s execution: the joints between variations. His durational analysis of the “Goldberg Variations” implies that performers should not pause between movements, or that the silences between movements should not be considered part of the performance. Don Franklin considers proportional relationships between tempi of successive movements in Bach’s music to be the norm; he argues that a fermata at the end of a movement indicates a break in the proportional continuity.[45] He notes that Bach places fermatas after eighteen of the thirty-two movements in the “Goldberg Variations,” creating groups of variations related by proportional tempi. Franklin is unusual among theorists of proportional tempi in his concern for the transitions between movements. However, he does not argue that proportional relationships should be maintained through entire works, rather focusing on smaller groups of movements or sections of music that he terms “temporal units.”[46]

Rink uses an architectural idea of proportional tempo to craft a performance of Brahms’s Fantasien op. 116.[47] Rink’s architecture is not derived from duration or phase fit, but from motivic correspondence between the pieces; he aims for motives that unify the set to be performed with equivalent durations, despite differences of notated value and tempo. Motivic relationships that can be highlighted by performance at proportional durations are taken by Epstein as score-based evidence that composers built proportional tempo relationships into their music.[48] Rink does not discuss local tempo modification, final ritardandi, or the silences between movements because prevailing tempo is the source of his architecture. This approach is the opposite of Gould’s scheme, which aims to substitute a rhythmic structure in the absence of motivic relationships and is primarily concerned with the transitions between movements.

Method

For the following analysis I used Sonic Visualiser[49] to quantify Gould’s rhythm in the 1981 and 1955 recordings of the “Goldberg Variations.” I tapped along with the recordings, then adjusted the markers while listening at 25% playback speed. I then converted durations between markers into bpm tempo measurements based on the inter-onset interval between two markers.

For reasons discussed above, especially Martens’s finding that Gould exerts greater control over listener’s embodied responses at the joints between movements in the 1981 recording, my analysis focuses on the transitions between movements. Gould has three tools at his disposal to craft these joints: proportional tempo, rhythmic continuity, and segue.

Proportional tempo is defined by the relationship of prevailing tempi of discrete sections of music; following Epstein I admit the ratios of 1:1, 1:2, 2:3 and 3:4. Epstein employs the concept of the Weber fraction (a common ratio of the just noticeable difference between two stimuli) to justify using 5% as the limit of just-noticeable difference between tempi.[50] For example, tempi between 114 and 126 bpm can be considered equivalent to 120 bpm.

Rhythmic continuity is the beat-to-beat connection over the boundaries between sections. I judge it to be present when the final tempo of a movement – based usually on the penultimate beat because the releases of the final notes are usually only rhythmically significant in the case of a segue – matches the opening tempo of the following movement at a 1:1, 2:1 or 3:1 ratio. I exclude ratios of 2:3 and 3:4 because I do not believe they are audible; psychological research to justify this position does not yet exist.

Segue is the avoidance of a pause between two movements. I judge segue to be present when there is no silence between movements, or when the silence is less than one beat in length, based on the final tempo of the preceding movement or the tempo implied by the continuation of a final ritardando one beat past the notated end of the movement. The silences between movements in studio recordings are often decided by producers rather than artists. However, Gould’s unique process in the recording studio, documented in the outtakes of Monsaingeon’s film and described by Forfia, specifically defined how the joints between movements should sound.[51] After each variation, Gould would define the gap by recording the first few measures of the following movement. Those measures, never intended to be included in the final product, served as a placeholder for use during the editing process. The amount of time between movements is consistent between the original LP edition and the CD reissue that I used for analysis.

In the Page interview, Gould hopes that “absolutely nobody actually notices what’s really going on”[52] as he crafts a structure based on tempo. The following analysis relies on many detailed observations, distinctions that are challenging for the average listener to register. The standard of relevance should be whether these timing effects were perceptible to Gould, and thus meaningful to his working process.

Large-Scale Tempo Shapes

Subtle but measurable slowing across large sections of music or entire movements is a common feature of Gould’s performance style, evident in many of his recordings including both versions of the “Goldberg Variations.” Large-scale slowing can be observed independently of final ritardandi. A linear model often fits the data well. Table 1 shows the prevalence of large-scale slowing across individual movements in Gould’s two “Goldberg” recordings. Percent slowing is calculated as the difference between a linear model’s predicted initial and final tempi, divided by predicted initial tempo (p < 0.05 in all cases).[53] To define a final ritardando, I identified the last inflection point in the tempo data for each movement, i.e., where acceleration turns to final deceleration at the end of the movement. I then removed the data following that point, up to a maximum of two measures in movements lasting thirty-two measures or one measure in movements lasting sixteen measures.

Table 1: Number of movements displaying large-scale slowing in Gould’s 1955 and 1981 recordings of the “Goldberg Variations”

Figures 2 and 3 exemplify Gould’s tempo shaping across whole movements. Tempo data is plotted as a series of connected points; a linear regression line is superimposed. The texture of variation 7 suggests a gigue, though Gould plays the movement rather slowly in both recordings. His tempo modulates by 17% in 1955 from about  = 65 to 54 bpm, and by 19% in 1981, from  = 58 to 47 bpm. The higher r² value combined with the flatter slope of the line is indicative of Gould’s more austere rubato in the 1981 recording.

Figure 2: Bach, “Goldberg Variations,” variation 7 (6/8); Gould’s 1955 recording, tempo chart, -beat (y = –0.19x + 65.9; r² = 0.30)

Figure 3: Bach, “Goldberg Variations,” variation 7 (6/8); Gould’s 1981 recording, tempo chart, -beat (y = −0.16x + 57.2; r² = 0.35)

That this kind of processual tempo change is common and yet has almost completely evaded comment is suggestive.[54] Processual slowing can be difficult to perceive. Alternatively, the notion of a basic tempo about which expressive deviations occur may be so ingrained in the way recent writers and performers discuss music that Hopkins and Bazzana avoided commenting on Gould’s large-scale shapes even when they were relatively obvious. Investigating the problem of determining basic tempo in expressive performances, Bruno Repp states “It might be argued that such performances do not have a basic tempo. This objection can be dismissed, however, because even highly expressive pieces are commonly preceded by metronome indications in the score.”[55] Cook criticizes the notion of a basic tempo as the “product of aesthetic ideology rather than of how performers actually played.”[56] Cook is referring to pianists on the earliest recordings, emphasizing pieces in which texture changes and generic references motivate pianists to express different characters via different tempi or tempo shapes. Gould is much more measured. His largest tempo modulations within a single movement in the 1981 recording are in variations 7 and 13: 19% and 21%. Part of the reason they are not notated in Hopkins’s transcription of Gould’s 1981 performance must be because no conventional notation exists for tempo changes of this sort. Furthermore, Gould’s discussion with Page suggests these slowdowns were not meant to be perceived as tempo modifications per se. I argue that their purpose is to create structural coherence for long passages of music.

Audio Examples 1 to 4 are some of the most pronounced examples of Gould’s large-scale slowdowns in the 1955 and 1981 recordings, paired with a transformed version that keeps the tempo more constant. In 1955 Gould played variation 20 (3/4, Audio Ex. 1) exceedingly quickly, but with a 20% slowdown across forty-five seconds. Beats were marked at a quarter note pulse. Again, a linear model fits the data very well, as shown in Figure 4 (r² = .46, p < .001). Audio Example 2 is the same movement with the linear tempo change removed.[57] In Audio Example 1, based on the trendline, Gould’s initial tempo is 144.8 bpm, slowing to 114.1 bpm. In Audio Example 2 the large-scale tempo shape has been removed so that the trendline is flat at 129.5 bpm. Listeners’ tendency to perceive rhythmic regularity in irregular patterns is well established in the psychological literature.[58] My ears struggle to interpret the difference in terms of tempo between the two Audio Examples, though the end of Audio Example 2 sounds oddly fast. The transformed example generally sounds more monotonous, while the original is lighter. In each reprise of the original version, I feel as though I am floating through the second half (mm. 9–16 and 25–32) before being gently set down.

Figure 4: Bach, “Goldberg Variations,” variation 20 (3/4); Gould’s 1955 recording; tempo chart, -beat (y = −0.31x + 146; r² = 0.77)

Audio Example 1: Bach, “Goldberg Variations,” variation 20 (Glenn Gould, The Goldberg Variations: The Complete Unreleased Recording Sessions June 1955,
Sony Classical CD 88843014882, this compilation ℗&© 2017, originally released 1955, CD 7, Track 21)

Audio Example 2: Bach, “Goldberg Variations,” variation 20, transformed (Glenn Gould, The Goldberg Variations: The Complete Unreleased Recording Sessions June 1955,
Sony Classical CD 88843014882, this compilation ℗&© 2017, originally released 1955, CD 7, Track 21; modified)

Audio Examples 3 and 4 are the first half of variation 16 (), the French Overture, in the 1981 recording. Once more the linear model fits well (Fig. 5: r² = 0.45, p < .001). The effect size is large: 27.3% slowing across sixty-eight seconds (62.6 bpm at the beginning to 45.5 bpm at the end). Beats were marked at a quarter note pulse. In Audio Example 4, Gould’s linear tempo shape has been removed so that the recording proceeds at about 54 bpm throughout. For me, the large-scale slowdown creates greater dynamism, a feeling of motion that I identify as a sense of musical structure. I feel as though I am being carried through the piece; I sense the origin, intermediate and final destinations, organizing my listening experience. In Audio Examples 1 and 3, Gould’s processual slowing activates in me a “mode of embodiment” that forces my perceptual participation in a large-scale gesture.[59] Obviously, the transformed examples are artificial; a pianist’s tempo is not independent of articulation, dynamics, and micro-level rubato. In addition, the tempo transformation results in some nuances that are inconsistent with Gould’s style, most notably the slowed-down speed of the quickest notes at the beginning of variation 16. Nevertheless, the comparison shows how a large tempo shape might evade verbal description while still being meaningful to listeners’ perception of the music. As with many other nuances of musical performance, listeners can feel the effects without being able to describe precisely their causes.

Figure 5: Bach, “Goldberg Variations,” variation 16, first half (); Gould’s 1981 recording; tempo chart, -beat (y = −0.29x + 63.2; r² = 0.45)

Audio Example 3: Bach, “Goldberg Variations,” variation 16, mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 17, 0:00–1:08)

Audio Example 4: Bach, “Goldberg Variations,” variation 16 (transformed), mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 17, 0:00–1:08; modified)

Most commentators have noted a relative reduction in tempo modification in Gould’s later recordings. Dale Innes perceives that Gould’s “tempos became more uniform later in his career, after he had left the concert stage,” and that “there is very little variability of tempo within each variation” in the 1981 Goldberg recording.[60] Bazzana argues that Gould’s later style shows “greater discrimination in the application of local rhythmic inflection.”[61] In his biography of Gould, Bazzana describes the later “Goldberg” recording as “considerably more calculated in terms of phrasing, balance, expressive nuance and ornamentation.”[62] For John Butt, Gould’s 1981 “Goldberg” recording “conforms like no other to what many see as the worst aspect of HIP, a musical high modernism that presents much of the music in a mechanical, equally detached and measured way.”[63] Hopkins, on the contrary, argues that “Gould introduced rubato in various instances in the 1981 recording, certainly more than in the 1955 recording.”[64] My tempo measurements suggest that the 1955 recording displays more rubato; the average coefficient of variation (CV) or relative standard deviation for the thirty-two movements is 8.2% in 1955 vs. 5.9% in 1981 (discounting final ritardandi, the average CV is 7.1% in 1955 and 5.2% in 1981).[65] Hopkins’s statement shows the division between measurement and perception of music in performance. In preparing an edition based on Gould’s performance, he may have been influenced by the question of notation, pondering what extent of tempo deviation demands inclusion in the score. The drier, more pointillistic sound quality of the 1981 recording may also make some instances of rubato more obvious.

In the 1981 recording, Gould’s large-scale slowing, more restrained rubato, and attention to rhythmic continuity at the joints between movements create a striking effect: tempo shapes that span multiple variations. In these multi-variation tempo shapes, proportional tempo relationships are effected through processual tempo changes. From the architectural point of view, comparing the beginnings of movements, the tempi of these movements are not proportional under Epstein’s definition.[66] In total, ten out of thirty-one joints in Gould’s 1981 recording feature a tempo shape that creates proportionality.

The first instance of tempo shaping across variations in the 1981 recording provides a simple example (Fig. 6, Audio Ex. 5). The initial tempo of variation 5 (3/4) is  = 164 bpm, which is not proportional at a 2:1 ratio with the initial tempo of variation 6 (3/8),  = 75 bpm, because the 9% difference exceeds the 5% limit defined by Epstein (see chapter Method above). Initial tempi are here measured as the average across the first two measures of each variation. However, the second half of variation 5 displays significant slowing irrespective of the final ritardando. Figure 6 shows Gould’s tempo at the transition between variations 5 and 6, with the tempo of variation 5 measured at the half-note level. The first half of variation 6 continues the slowing from the second half of variation 5. This joint lacks both rhythmic continuity and segue. Proportional tempo is the only unifying force at work here, and it emerges from Gould’s processual tempo change.

Figure 6: Bach, “Goldberg Variations,” variation 5 (3/4), second half, through variation 6 (3/8), first half; Gould’s 1981 recording;
tempo chart, -beat (variation 5), -beat (variation 6) (y = −0.25x + 83.0; r² = 0.50)

Audio Example 5: Bach, “Goldberg Variations,” variation 5, mm. 17–32 and variation 6, mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 6, 0:17–0:37 and Track 7, 0:00–0:13)

Though Gould’s notebook page and his comments in the Page interview suggest he constructed the transitions based on the audible correspondence of surface-level note values, his precision at the joint between variations 11 and 12 implies a sensitivity to less-audible proportional relationships (Audio Ex. 6). In variation 11 (12/16) Gould slows the tempo from an average of  = 147 bpm in the first two measures to about 140 bpm before the final ritardando; in variation 12 (3/4) Gould slows from an average of  = 91 in the first two measures to 89 bpm before the final ritardando. The proportional tempo relationship between variations 11 and 12 depends on those slowdowns. The initial tempi are not proportional – 147:91 bpm. But the final tempo of variation 11, discounting the ritardando, fits proportionally with the initial tempo of variation 12 – 140:91 bpm, or 3:2 (2.5% deviation from the exact value 140:93.33 bpm). Figure 7 illustrates the joint. Note that the tempo for variation 11 is a proportional transformation of the data; the hypothetical note value charted is 1.5 times the dotted eighth, that defines the tactus, or 4.5 sixteenth notes.[67]

Figure 7: Bach, “Goldberg Variations,” variation 11 (12/16), second half, through variation 12 (3/4), first half; Gould’s 1981 recording;
tempo chart, -beat x 4.5 (variation 11), -beat (variation 12) (y = −0.095x + 97.6; r² = 0.60)

Audio Example 6: Bach, “Goldberg Variations,” variation 11, mm. 17–32 and variation 12, mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 12, 0:26–0:53 and Track 13, 0:00–0:31)

Figure 7 implies rhythmic continuity between the last beat of variation 11 and the first beat of variation 12; that continuity is not audible because the plotted pulse rate for variation 11 is not audible at the surface level. The 4.5 sixteenth-note pulse in Figure 7 also means that the rhythmic continuity implied between the last beat of variation 11 and the first beat of variation 12 is not audible. However, Gould could easily have slowed a bit more at the end of variation 11, or started variation 12 closer to the prevailing tempo, to match either the variation 11’s dotted eighth to variation 12’s quarter or the sixteenth to the sixteenth across the break. Hopkins claims that the sixteenth-note pulse at the end of variation 11 matches the sixteenth-note pulse at the beginning of variation 12.[68] I believe he is responding to the proportional tempo relationship. Gould plays the last three sixteenths of variation 11 (m. 32.3) at a rate of 0.2 seconds per note, but begins variation 12 (m. 1.1) at a rate of 0.175 seconds per note; this deviation of 12.5% is too great for the passage to be considered rhythmically continuous. At 0.73 seconds long, the intermediate pause feels like a continuation of the final ritardando in variation 11, and nearly matches the first beat of variation 11 (0.7 seconds). As noted above, these intermediate pauses were defined by Gould during the recording process. Gould binds the two variations together with a large-scale tempo shape and a segue. The sense of proportional tempo between variations 11 and 12 depends on the tempo shape. To my ear, Gould achieves a clear and satisfying change of character for the beginning of variation 12 without sacrificing the continuity provided by a proportional tempo relationship.

The connection between variations 12 and 13 shows an even more dramatic example of proportional tempo dependent on large-scale tempo shape (Fig. 8, Audio Ex. 7). Figure 8 illustrates the joint. Gould avoids rhythmic continuity and segue; with 2.6 seconds of silence between the sharp release of the last note of variation 12 and the initial attack of variation 13, the gap is one of the longest in the audio recording. In the video version, Gould’s timing of this transition is almost identical to the audio recording; he can be seen conducting an upbeat before he begins variation 13. This upbeat is in the opening tempo of variation 13. Perhaps Gould is remembering the tempo of variation 12 before the final ritardando. Proportional tempo is the only force binding these two variations together, and this proportionality again depends on large-scale slowing. The initial tempi of 93 (quarter beat of variation 12, 3/4) and 85 bpm (eighth-note beat of variation 13, 3/4) are not within the 5% margin of just-noticeable difference (deviation 9.4%), and the prevailing tempo of variation 13 is even slower.

Figure 8: Bach, “Goldberg Variations,” variation 12 (3/4), second half, through variation 13 (3/4), first half; Gould’s 1981 recording;
tempo chart, -beat (variation 12), -beat (variation 13) (y = −0.15x + 93.7; r² = 0.49)

Audio Example 7: Bach, “Goldberg Variations,” variation 12, mm. 17–32 and variation 13, mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 13, 1:03–1:38 and Track 14, 0:00–1:13)

Gould’s pronounced slowing in the first half of variation 13 might appear to be a compromise, seeking to make a smooth tempo connection with the preceding variation. But Gould’s tempo shapes in the 1955 and 1981 recordings are remarkably consistent, as shown in Figure 9. While Gould in his 1981 recording uses small-scale ritardandi and accelerandi that were not present in the 1955 recording to create rhythmic continuity between variations, he never employs a large-scale slowdown unless it had already been conceived in the 1955 recording. The presence of tempo shapes across the joints between movements in the 1981 Goldberg recording is a consequence of Gould’s efforts to fit the beginning of each movement to the end of the preceding movement, avoiding an exaggerated impression of finality at the end of each movement. The basic consistency between the two recordings suggests that Gould did not consciously manipulate large-scale tempo shapes within variations to create continuity in the 1981 recording. For Gould, therefore, increased coherence in the 1981 recording is primarily a function of what happens at the transitions between movements.

Figure 9: Bach, “Goldberg Variations,” variation 13 (3/4); Gould’s 1955 and 1981 recordings; tempo chart (-beat)

Gould’s tempo shapes are integral to his concept of the individual variations in which they occur; they are not compromises that facilitate proportional relationships at the macro level. As observed above in variation 13, some of Gould’s more extreme tempo shapes might seem to be motivated by a desire to match tempi at the joints between movements. In variation 15 Gould slows from  = 48 bpm at the opening to 35 bpm at the end of the first half; in the repeat of the first half and in the second half Gould’s tempo centers around 40 bpm. Variation 16 exhibits a similar shape, with large-scale slowing in the first half followed by a more consistent tempo in the second half. But like variation 13, Gould’s tempo shapes in variations 15 and 16 in the 1955 and 1981 recordings are similar; slowing in the first half was part of his concept of the piece irrespective of his desire to effect global continuity. Where tempo shapes diverge between the two recordings, Gould employed a more consistent pulse with less rubato and less large-scale slowing in 1981. In this later recording, Gould actively manipulates the perception of continuity through his choice of tempi and careful timing of transitions. Large-scale tempo shaping within variations is a feature of his style throughout his career, not something he added or increased in the 1981 “Goldberg Variations” recording.

Figure 10: Typology of proportional tempo relationships dependent on tempo shaping in Gould’s 1981 “Goldberg Variations”

Figure 10 categorizes Gould’s use of proportional tempo and tempo shaping in the 1981 recording. The asterisk marks the special case of variations 19–20, in which the tempo shape is clearly perceptible but does not create proportionality. In the other ten cases involving tempo shapes, proportionality depends on the tempo shape; initial tempi of the paired variations are not proportional or, in the case of a tempo shape in the following variation, the final tempo is not proportional to the main tempo of the preceding variation. For example, in variations 14–15 (Fig. 11) and 29–30 a tempo shape in the following variation pushes both the final and average tempi out of proportion with the preceding variation’s constant tempo. Only three joints feature a proportional relationship between initial tempi that is undermined by a tempo shape. The transition between variations 7 and 8 features a segue and a particularly strong use of rhythmic continuity. In the penultimate beat of variation 7 (6/8), the eighth notes at 110 bpm equal variation 8’s (3/4) quarter note pulse; the implied eighth notes of the final beat of variation 7 at 76 bpm equal the following dotted quarter pulse, accentuated by Gould’s left hand (Audio Ex. 8). Proportional tempo is not the main force responsible for continuity at the joint.

Figure 11: Bach, “Goldberg Variations,” variations 14 (3/4) and 15 (2/4, first half); Gould’s 1981 recording; tempo chart -beat (variation 14), -beat (variation 15)

Audio Example 8: Bach, “Goldberg Variations,” variation 7, mm. 30–32 and variation 8, mm. 1–8
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 8, 1:07–1:16 and Track 9, 0:00–0:13)

Variations 10 and 20 have weak tempo shapes – less than 5% – that cause their final tempi to just miss proportionality with the initial tempi of variations 11 and 21. None of the three cases in which tempo shape undermines proportionality is strong evidence for the architecture view of proportional tempo. Under Epstein’s phase-fit view, only eight pairs of movements feature proportional tempo relationships. For me as a listener, proportional tempo is audible in far more than a quarter of the cycle.

Gould’s tempo shape for variations 19 and 20 deserves special comment, as variation 19 is the only movement in which Gould employs large-scale acceleration (Fig. 12, Audio Ex. 9). In Figure 12, tempo values for variation 19 are proportionally transformed. Variation 19 starts at  = 90 bpm, proportional to variation 20 ( = 120 bpm) at a 3:4 ratio. Proportionality of tempo is undercut by subtle acceleration through variation 19: the initial tempo (89 bpm in the first two measures), rather than the final tempo (93 bpm in the last measure), of variation 19 is a better fit with the initial tempo of variation 20 (120 bpm) though both are within the 5% limit. The acceleration through variation 19 creates a sense of expectation. Instead of rewarding that expectation with the smoothest, most logical tempo to start variation 20 ( = 94, perhaps) Gould chooses a tempo proportional to a 3:4 ratio to effect a sudden burst of energy while maintaining continuity. Using variations 19–20 as an example, Bazzana notes that Gould can “‘trick’ the listener into perceiving a sense of tempo continuity where, mathematically, there in fact is none.”[69] My view is that Bazzana’s ears are correct: Gould creates a feeling of proportionality. The mathematical logic that underpins the continuity is only clear through precise data.

Figure 12: Bach, “Goldberg Variations,” variations 19 (3/8) and 20 (3/4); Gould’s 1981 recording; tempo chart, -beat x 1.5 (variation 19), -beat (variation 20)

Audio Example 9: Bach, “Goldberg Variations,” variation 19 and variation 20, mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 20 and Track 21, 0:00–0:24)

Gould heard tempo shaping as a structural force. He avoided utilizing his entire arsenal of techniques for creating continuity at the same joint. Proportional tempo, rhythmic continuity, and segue occur at the same joint only ten times. Usually these joints do not involve a tempo shape; the exceptions are variations 7–8 and variations 19–20. In both of these cases, described in detail above, the tempo shape undermines the sense of proportional tempo. When Gould uses rhythmic continuity and proportional tempo dependent on tempo shaping at the same time, he balances those forces with a long pause, for example in the transitions between variations 23–24 and 24–25. Four cases show proportional tempo dependent on a tempo shape in the absence of segue and rhythmic continuity. These examples – transitions between variations 5–6, 12–13, 14–15, and 15–16 – are a strong point against the architectural idea of proportional tempo as a structuring force, as proportional tempo dependent on shape is the only binding agent at these transitions. Furthermore, the transitions between variations 12–13, 14–15, and 15–16 feature some of the most striking changes of character in the cycle. For Gould, the tempo shape seems to be the preferred way to create continuity between diverse materials. For Utz the extreme tempo contrasts between variations 4–5, 7–8, 13–15, 20–22, and 24–26 effect discontinuity, enhancing the listener’s sense of “spatialized” or architectural time.[70] Of these variations 7–8, 14–15, and 24–25 feature proportional tempi dependent on tempo shaping, while variations 4–5 and 20–22 feature proportional constant tempi to balance the discontinuity.

Gould often uses a tempo shape in the absence of rhythmic continuity. The tempo shapes across the boundaries between movements are not a function of beat-to-beat manipulation. The prevailing tempo upon which Gould based his proportional plan, the axis about which he performed accelerando, ritardando, and various kinds of rubato, is a slant rather than a constant level. The joints that show tempo shaping without rhythmic continuity are variations 5–6, 10–13, 14–16, and variation 30 into the Aria da capo. In all these cases, Gould avoided an easy way to achieve greater structural unity through rhythmic continuity. Contrast of character and local closure through a pronounced ritardando here seem to have been more important than maximal continuity.

Gould’s interview with Page gives no indication that he was aware of these large-scale tempo changes within variations. He describes a tempo equivalence between the beginning of variation 16 and the fugal second half of that variation.[71] This equivalence is supported by the data: the overture’s opening sixteenth equals the fughetta’s eighth note; more relevant, however, is the rhythmic continuity between the end of the first and the beginning of the second half. The prevailing tempo at the end of the overture section does not match the tempo of the fughetta. On the contrary, Gould’s description of the joint between variations 16 (3/8) and 17 (3/4) is accurate; the tempo is unusually stable in variation 17 and the second half of variation 16.

In the interview, Gould claims an equivalence between the quarter note of variation 17 (3/4) and the half note of variation 18 () without referring to specific passages in either variation. In fact, the continuity between these variations is based on the ritardando at the end of variation 17. The initial tempi are  = 109 bpm in variation 17 and  = 95 bpm in variation 18 which is not a proportional relationship. Gould forges this kind of connection – with rhythmic continuity and segue, but no proportional tempo relationship – at five joints between movements. The fact that Gould chose this joint as one of only a few examples of his proportional tempo system illustrates a divergence between his theoretical and practical approaches. There is no reason to believe Gould was being disingenuous in the interview, but the evidence of his performance shows that he chose his tempi based on his experience of playing and listening to music rather than on any intellectual idea of tempo proportion. In fact, his verbal descriptions are sometimes misleading.

Continuity as an Expectation

Clearly Gould did not seek the greatest possible continuity at every joint between movements in his 1981 “Goldberg” recording. In shaping the transitions, Gould balances the demands of characterization, local closure, and global continuity. When Gould pauses between variations, especially for durations that cannot be construed as beats continuing the preceding or anticipating the following tempo, this must be regarded as a deliberate decision to weaken the continuity between variations. The same logic applies to rhythmic continuity, which can always be achieved given a sufficient tolerance for final slowing or initial acceleration. Even the absence of a proportional tempo relationship between successive variations must be regarded as deliberate, especially considering Gould’s desire for a “constant rhythmic reference point.” Mathematically, the chance of finding a proportional tempo relationship given Epstein’s ratios, a 5% tolerance of difference, and randomly selected tempi is 43%. Factoring in Gould’s ability to change tempo processually, conservatively estimated as up to 10% slowing, that probability increases to 77%. Gould uses proportional tempo and rhythmic continuity as an expectation to be contradicted for expressive purposes.

In the film version of the 1981 “Goldberg Variations,” Gould’s body language and conducting provide evidence for his interpretation of the pauses between variations. He never conducts more than one beat, and that beat is always an upbeat in the tempo of the following variation. Sometimes his sharp release of the last note of a variation marks a temporal division. However, Gould never articulates the silences between variations in a way that suggests strict rhythmic continuity. In several places in the film and record versions, the silence between movements is easily divided into a series of beats that continue the pulse from the end of one variation into the beginning of the next. However, this does not seem to have been Gould’s intention based on his body movements in the film: in Video Example 1, Gould conducts one beat in a pause which clearly accommodates three beats of the final tempo of variation 12. Many variations start directly after the preceding variation (segue), but Gould always delays slightly before the new first beat – despite the fact that the delay weakens rhythmic continuity.

Video Example 1: Bach, “Goldberg Variations,” variation 12 (mm. 17–32) and variation 13 (mm. 1–8)
(Bruno Monsaingeon / Glenn Gould, The Goldberg Variations [Glenn Gould Plays Bach], Sony Classical DVD 88691975049 03, 1:56–3:00)

The first transition on the audio recording illustrates how Gould balances variety and continuity (Audio Ex. 10). Hopkins surmises that Gould referred to this transition when he described tempo “modifications which take their cue from ritards at the end of the preceding variation” in the Page interview.[72] The ritardando that ends the Aria is steep and long; it perfectly matches the beginning of variation 1 through rhythmic continuity. The transition sounds like an extremely deliberate tempo modulation. Gould may have considered the tempo of variation 1 to be proportionally unrelated to the tempo of the Aria. Certainly his rhetoric privileged audible matching of note values, though a proportional relationship may have subconsciously guided his tempo choice. The first half of the Aria shows strong tempo shaping, while the second half is steadier. Given the amount of tempo modification in the Aria, the constant-tempo stretch in the second half between measures 26 and 29 at  = 65 bpm is the best estimate of a prevailing tempo. Variation 1 is the most metronomic of the set, at  = 83 bpm, creating a 3:4 proportion (4.4% deviation). 3:4 is the highest order ratio under Epstein’s definitions; nevertheless, the transitions between variations 12–13 and 20–21, which show little or no rhythmic continuity and a tempo proportion of 3:4, suggest that Gould heard 3:4 relationships as proportional and used them in his tempo plan. In the first transition, a strong force of rhythmic continuity balances a proportional tempo relationship weakened by rubato.

Audio Example 10: Bach, “Goldberg Variations,” Aria, mm. 25–32 and variation 1, mm. 1–16
(Glenn Gould, Bach: The Goldberg Variations, CBS Masterworks CD MK 37779, ℗&© 1982, Track 1, 2:16–3:05 and Track 2, 0:00–0:34)

Twice in the recording Gould avoids proportional tempo, rhythmic continuity, and segue between variations, creating a major break. Variation 25, the final G minor movement, is by far the longest and slowest in the set. The unifying tempo plan of the last five variations compensates for this cessation of motion and continuity at the end of variation 25: Gould plays variations 26 through 30 without a break; every joint features rhythmic continuity. Three of the four joints are also marked by proportional tempo relationships. The other major break follows variation 13, the third slowest movement in the recording. Here Gould seems to be compensating for the strong tempo relationships between variations 9–13 – all marked by proportional tempi, with three of four joints played with segue – and between variations 14–17 – again all related by proportional tempi. Even more striking is the tempo shaping in variations 11–13 and 14–16. The break at the end of variation 13 seems to balance the continuity created by proportional tempo dependent on large-scale slowing. As Repp states in his review of Epstein’s Shaping Time: “One is led to wonder whether a violation of tempo proportionality may not also create pleasurable tension or desirable contrast between movements.”[73] Epstein’s theory, and architectural tempo plans for the “Goldberg Variations” such as Schenkman’s or Siegele’s, suggest maximal use of proportional tempo relationships. Gould’s execution shows the role of variety.

Bach’s Structure, or Gould’s?

Bach’s compositional markers of large-scale structure show little relationship with Gould’s tempo plan. Generative theories of performance suggest that deeper structural boundaries will be marked with greater phrase-final lengthening, the musical corollary of the tendency in human speech to slow down at the end of a sentence.[74] Gould’s body language in the film version implies that he considers the silences between movements to be integral to the performance. Thinking of final lengthening broadly as cessation of motion, breaks between variations that feature both significant final ritardandi and longer silences might be interpreted as markers of structural segmentation. This might explain both the huge ritardando – 43% of tempo over the final eight measures – and the four-second gap that lead from variation 15 to 16 in Gould’s 1981 audio recording. Variation 16 marks not only the middle of the work by number of movements, but also signals a new beginning through its reference to the French Overture genre. A similarly large ritardando – slowing by 45% over five very slow measures – at the end of the Quodlibet (variation 30) and three-second gap prepare the return of the Aria da capo at the end of the cycle. Several of Gould’s pauses are preceded by modest ritardandi. The longest gaps between movements on the recording both prepare the G minor movements for which Bach provided slow tempo markings: variations 15 (Andante) and 25 (Adagio). The only other silence longer than two seconds is before variation 13, another slow movement. In these examples the dissipation of energy between fast and slow tempi seems to motivate the gap, rather than any structural consideration. Still, the combination of a large ritardando and a lengthy pause divides the structure in two at the highest level.

The most obvious score-based division of the “Goldberg Variations” is into groups of three, ending with a canon. Gould does not treat these divisions in a systematic or unusual way. The variety of strategies between the ends of the canons and the beginnings of subsequent variations are as diverse as his strategies for the cycle as a whole.

Occasionally Gould’s interpretation seems to conflict with Bach’s notation. Bazzana notes “compromises with historical dance tempi” in variations 7 and 19, as well as suppression of final slowing in variations 19, 21, and 27.[75] In variation 7, Gould was certainly aware of the tempo marking “al tempo del giga” indicated in Bach’s Handexemplar; Bazzana notes that Gould can be seen with the 1979 Henle edition, which uses the Handexemplar as a source, on outtakes of the film version of the 1981 recordings. Gould’s slow tempo of variation 7 can be interpreted as a break with Bach’s instructions. In variation 19, Gould’s tempo and large-scale accelerando are surprising, but exceptional in the context of the recording as a whole. In variations 21 and 27, he accelerates only after the final cadence. He treats the last few notes as a lead-in to the following variation without undermining the local sense of closure.

Within individual movements, Gould’s tempo shaping is not supported by Bach’s compositional plan. Lawrence Dreyfus and Karol Berger argue that the ordering of musical materials in a piece was Bach’s least important compositional decision.[76] Rather than conceiving of a piece as a teleological process, Bach crafted various polyphonic combinations (labeled “inventions” by Dreyfus); their ordering in the final composition was largely incidental. In each individual “Goldberg” variation, repetition of the Aria’s bass line might seem to limit the possible measures into which an invention might be placed. However, Bach included so much internal repetition and sometimes substituted bass notes, so this constraint is largely nullified. Yet for Gould – with his large-scale tempo shapes, accelerandi at the opening of variations, and ritardandi calibrated to create rhythmic continuity – placement of material at the beginning, middle, or end of a variation has a direct impact on the tempo of its execution. At the upper limit, these are differences of 15–20% of tempo.

Dreyfus’s and Berger’s arguments about Bach’s disposition of materials apply at the large scale as well. In an analysis that does not cite Dreyfus, Peter Williams argues that the variations are, “apart perhaps from the last five, not as continuous and their order not so inevitable as might be commonly supposed.”[77] Many aspects of the ordering of movements in the “Goldberg Variations” are clearly not random: the French Overture at the midpoint of the cycle, the ordering of the canons. But even these highly determinative aspects of the structure undermine the sense of large-scale progression. The French Overture signals a new beginning in the middle of the work, implying a cyclical concept of time. The progress of the canons is difficult to perceive aurally. Their accompanying bass line conceals their difference from the figural variations; many of the figural variations feature imitative elements that confuse their difference from the canons. Berger argues that by increasing the interval of imitation in the canons past the seventh or the octave, Bach represents the potential of infinite growth: “with the return of the initial Aria at the end of the cycle, the potentially infinite cycle turns into a circle.”[78]

The sequence of variations is a critical component of Gould’s tempo decisions. The tempo of his Aria da capo is not identical to the opening Aria; the cycle ends in a different place from where it began. The heard sense of structure is not based on architecture – each variation’s reference to the Aria – but on the teleological process of Gould’s performance.

Conclusion

The importance of the 1981 “Goldberg Variations” recording in Gould’s œuvre has been exaggerated, even mythologized, due to its accidental status as his last recording. The interview with Tim Page has provided perhaps more grist for the mill of criticism than the actual sound of the recording. But as Gould often expounded the theoretic underpinnings of his performance decisions – with a degree of obfuscation and exaggeration – viewing his 1981 “Goldberg Variations” as exceptionally polemical or dogmatic in support of his tempo theory is mistaken. Gould’s interest in tempo as a unifying force was already evident in the 1970s, especially in his recordings of Bach’s English and French Suites. Bazzana notes that some of his latest recordings are his most sophisticated in terms of rhythmic unity in multi-movement works: Beethoven’s Sonatas op. 26 and op. 27, no. 1 (1979 and 1981), and Bach’s Partita No. 5 in D major (1979).[79] The 1981 “Goldberg Variations” are far more complex and subtle than some of his earlier experiments using tempo to generate large-scale form: the finale of Beethoven’s Sonata op. 110 (1956) with its doubling of pulse rate between sections, and Bach’s Prelude and Fugue in E major from The Well-Tempered Clavier I (1962) with a less precise increase of tempo in each section. Perhaps Gould’s ideas about unifying tempo structures would have evolved further had he lived longer. But if the 1981 “Goldberg Variations” are not a summation, they at least represent his point of furthest development rather than a sidetrack.

The effectiveness of Gould’s plan is based on a feeling “in his bones” quite literally, as his recording practice involved playing along with the preceding movement to find the tempo for each variation. His memory for pulse rate seems to function at a middle-ground level, as Gould is able to accurately match tempi that have undergone processual change through a movement, discounting sometimes-long final ritardandi. In several cases he even matches the rate of tempo change from the second half of one variation to the first half of the next. Gould’s performance, particularly his large-scale tempo shaping, shows that proportional tempo relationships and the feeling of affective difference created by a new section in a new tempo are not mutually exclusive.

Gould’s tempo plan in the 1981 “Goldberg Variations” is anachronistic. His interest in unifying multi-movement works is distinctly modernist: rooted in Schoenberg’s rhetoric of organic unity, it parallels metrical techniques developed by Igor Stravinsky and Elliott Carter. Gould’s structure operates in an area underdetermined by Bach’s notation. Though Bazzana has described Gould’s relationship with Romanticism,[80] much recent scholarly work on Gould emphasizes and develops his technological rhetoric.[81] Butt hears Gould’s 1981 “Goldberg Variations” as hyper-modern,^[82] yet Gould’s rhythm is, at its roots, not mechanical. Much as pianists on the earliest recordings often sought unique and individual readings of a canonical score, irrespective of the composer’s intention, Gould imposed structure on the “Goldberg Variations.” Rink has argued for a concept of musical structure that is “constructed, not immanent […] pluralistic, not singular.”[83]

The structure that Gould constructs is not based so much on a parsing of Bach’s materials – determination of the greater or lesser significance of various events in the score – but on a powerful force of continuity. Gould’s rhythm compels his audience to listen. That continuity, a kind of thread that through the twists and turns of the performance never quite loses tension, is a listener’s sense of large-scale structure. Martens showed how listeners’ embodied responses to Gould’s rhythm were less diverse when listening to his 1981 compared to his 1955 recording.[84] Our continuing fascination with the 1981 recording must be based, at least in part, in the control Gould exerts over our perception.

In a 1974 interview Gould shared his attraction to Artur Schnabel’s structural sense of rhythm:

Schnabel was aware of the pulse of the paragraph. He was certainly aware of the interior pulse as well, but he chose to let it ride through the paragraph, as if he were dictating a letter with a certain series of commas and semicolons, and I don’t think anyone else ever played the piano using that system successfully – other people have tried, but nobody else ever really got it.

I’m thinking of one gorgeous record, Opus 2, no. 2, in which you are really not aware of the bar line, and in which the structure of the piece could not be more plastic – it’s utterly clear – but there’s no sense of the sort of vertical tension that I, for example, would automatically try to bring to the piece. I would play with very firm, very tight rhythmic features. But Schnabel doesn’t. He makes you feel that you’re floating through an entire paragraph, and that when you get to the end of that paragraph, no momentum has been lost.[85]

Gould’s 1981 “Goldberg Variations” represent a synthesis of his own “vertical tension” with Schnabel’s clarity at the level of the paragraph. Gould’s large-scale tempo shaping is what allows him to achieve closure at the end of a variation without losing momentum as he continues to the next movement. We hear metronomic accuracy in Gould’s rhythm, and Gould himself says of Schnabel’s rhythmical flexibility: “I don’t do it at all.”[86] Leech-Wilkinson and Cook have argued that statements about performance cannot be taken at face value;[87] studies like Dorottya Fabian’s and Emery Schubert’s show divergence of perception and empirical measurement of performance timings.[88] In this case, a dialogue emerges between Gould’s conceptual understanding of his playing and his deep-seated intuition about the rhythmic delineation of musical structure. That intuition was founded on, or at least reinforced by, his teenage obsession with Schnabel’s records.[89]

Though it is but one example, Gould’s 1981 “Goldberg Variations” suggest that in practice proportional tempo works very differently from how it is described in the theoretical literature. Perception of proportional tempo relationships is more about treatment of transitions than about durations or average tempi of entire sections. In Gould’s “Goldberg Variations” performance, the moment-to-moment progression of tempo creates large-scale structural coherence. Furthermore, the dichotomy between Gould’s architectural description of his tempo plan and its processual execution highlights the difficulty of bridging the divide between verbal descriptions of music and the actual sounds. Given the sustained scholarly and popular attention on Gould’s recordings, other structurally determinative performance practices must also lurk outside of the written record.