“There is a natural chromatic order, existing of itself, by virtue of the almighty power of Number. It belongs to all, and it can work for anyone” – Jenny McLeod, 1989[1]

Tone-clock theory (TCT) is a recent and underexplored development in contemporary post-tonal harmony that functions as a map of twelve newly discovered chromatic tonalities, provides composers, improvisors, and theorists with an alternate framework through which to understand and engage with the entire chromatic realm, and leads to the creation of innovative compositional and analytical techniques. TCT is based upon the twelve notes of the chromatic scale, which are organized around a clock module with each ‘hour’ denoting a specific chromatic tonality based around their interval-classes (IC). These tonalities are established around twelve possible chromatic triads, or trichords, and can be used to generate, among other things, a series of non-repeating twelve-tone collections that are ordered by their ICs, known as ‘harmonic fields,’ through a transformational action called the ‘steering principle’ that establishes the harmonic character of each hour. The clock face itself functions as a map by which composers and improvisors can navigate each tonality for application in their creative work. One of the challenges when researching this theory is not only the lack of published material, but also that there are at least two identifiable versions of it, namely its original incarnation as codified by Dutch composer Peter Schat (1935–2003), sometimes referred to as ‘classic’ tone-clock theory,[2] and its expanded version by New Zealand composer Jenny McLeod (1941–2022), which has significantly more theoretical detail. The bulk of published research thus far has been focused on the original ‘classic’ version, while little has been written about expanded TCT.

As this is a new and developing harmonic system, it has existed in a state of flux since its codification. One of the reasons for its obscurity can be attributed to the fact that not only has little been written about it, but there has also been some disagreement over terminology, leading to confusion over its operations. Articles on this subject often employ differing systems of analysis depending on whether they are using either Schat’s approach, whose writings are often more vague, esoteric, and philosophical rather than scientific, or McLeod’s, which is much more specific and theoretically rigorous.

As TCT’s has its own unique terminology and notational system that relies heavily on a set of short-hand symbols, mostly involving Roman numerals, other theorists have sometimes attempted to hybridize it with established post-tonal concepts, most notably Forte’s pitch-class (PC) set theory, David Lewin’s transformational networks,[3] or to invent their own terminology and means of analysis entirely.[4] As such, this article has two primary purposes, namely to 1) clearly explain the theoretical workings, notational practices, and historical context of ‘classic’ tone-clock while touching on a few key concepts of McLeod’s expansion and 2) to compare the notational practices of these two systems and to establish a consistent terminology and analytical methodology. I will attempt to explain the functions of TCT using the terminology and processes of its founders and to show how it can function independently as a fully developed harmonic theory that does not need to be adapted to another. An understanding of these principles is also vital for any future analysis of tone-clock specific compositions, as well as any creative application to contemporary composition or improvisation.

HISTORY OF TONE-CLOCK THEORY

Since its official codification in 1982, there have only been two prominent practitioners of this theory in contemporary composition: Dutch composer Peter Schat and New Zealand composer Jenny McLeod. While it was Schat who developed the foundational principles of TCT, published in a series of articles that are collected in his book De Toonklok (1984), it was McLeod who vastly expanded it to encompass all of chromaticism, which she catalogued exhaustively in her unpublished book Tone Clock Theory Expanded: Chromatic Maps I & II (1994). In doing so, she discovered new forms of modulation, tonal organization, and compositional practices specific to TCT, which she developed through her 24 Tone Clock Pieces (1988–2004) for solo piano. Furthermore, her book also presents an alternative theoretical framework to Allen Forte’s PC set theory, as he outlined in The Structure of Atonal Music (1973). McLeod systematically examines each of Forte’s 220 PC sets and reframes their descriptions using Schat’s interval-based approach, while also cross-referencing each entry with other prominent chromatic theories, such as those of composers Olivier Messiaen, Pierre Boulez, Milton Babbit, and Iannis Xenakis.[5]

TCT was perhaps best described by McLeod in her introduction to the English language reprinting of Schat’s book The Tone Clock (1993) as a “twelve-note harmonic system [and] also a chromatic ‘map’, a tool providing a systematic and comprehensive view of the whole chromatic territory.”[6] Composer and professor Michael Norris of the New Zealand School of Music at Victoria University of Wellington further defined it as “an attempt to develop a systematic approach to chromatic composition.”[7]

Schat, like McLeod, was a former student of Pierre Boulez, and was driven to move past the compositional methodologies of serialism by 1967, claiming that “the organization of all parameters in music was a compositional ‘dead end’ and refocused his efforts towards an interval-based system,”[8] for which he laid out the premise in his essay Circular Fragment of a Theory (1966)[9]. Schat’s primary goal in the creation of the tone-clock was that it function not exclusively as a compositional methodology (as he hated “recipes of how to compose” finding them to be “mostly unreadable, boring, and always humorless”[10]), but as a map of new and unexplored chromatic tonalities, demonstrating “that there is a natural chromatic order […] [that] belongs to all, and […] can work for anyone.”[11] While the credit must go to Schat for originally codifying the foundational principles of TCT, it was McLeod who composed the first official piece of tone-clock music in 1968 with Earth and Sky. She makes this point in a footnote in her book, asserting that it was “the earliest pure tone-clock composition, whose organizational basis is consistently and broadly the steering of one hour by another, different hour,”[12] a claim that was corroborated by John Croft in his analysis of the piece in 1993.[13] The reason for this is that as both Schat and McLeod had studied with Boulez, they had absorbed the same theoretical material that provided the basis for TCT’s development, resulting in the two strains of the theory developing parallel, yet independently of each other before their first meeting in 1987 at a conference in Louisville, Kentucky. While McLeod had worked with TCT creatively long before Schat, it was only in her early pieces, notably Earth and Sky and Under the Sun (1971), shortly after which she took an extended hiatus from composition, returning to her work in the early 80’s.[14] When Schat introduced her to the systemic approach he had developed, she quickly recognized the same principles that provided the basis for these early works but as “there was next to no musical terminology with which to describe this material succinctly” she had “simply forgot what [she] had done.”[15] It was Schat’s initial codification of TCT which inspired her to revisit her earlier work and begin developing her expanded theory.

Two important distinctions between TCT and previous approaches to twelve-tone composition are that 1) while “typically [TCT] uses all twelve chromatic pitches […] it does not have to,”[16] as it was designed to have a level of creative freedom that Schat felt was not possible within serialist methodologies and 2) whereas twelve-tone music is usually organized around individual pitches and related PC collections, TCT is instead based on the intervallic relationships between the pitches as ICs. This important distinction places TCT’s creative application more in line with Messiaen’s modes of limited transpositions than the tone rows of Arnold Schoenberg and the Second Viennese School.

BASIC PRINCIPLES OF TONE-CLOCK THEORY

In brief, the tone-clock is an organizational tool which maps out twelve chromatic tonalities and organizes them around a clock module by ‘hour,’ each based around one of twelve possible chromatic ‘triads’ (Forte’s ‘trichords’) that can be transposed (or ‘steered’) to generate a non-repeating twelve-tone harmonic field that defines that tonality. These chromatic triads are defined by their IC and ordered around the tone-clock from their smallest intervallic distance between pitches (in semitones) <1+1> to their largest <4+4>, each having a unique harmonic ‘flavour’ that defines their chromatic tonality. The fully mapped out clock module is referred to as either the ‘Zodiac of the Hours,’ or ‘Zodiac of the Tonalities,’ and displays graphical representations for each hour tonality that serve as a guide for composers (or improvisors) to navigate them in their creative work.

Although TCT has its theoretical roots in contemporary harmonic developments such as the serialist methodologies of Schoenberg, Webern, Boulez, and most importantly, Messiaen’s modes of limited transposition, Schat’s system avoids many of the strict transformational rules and terminology associated with these compositional and analytical approaches. For example, Schat and McLeod are adamant that these chromatic tonalities, and any other resulting collection, be referred to as ‘harmonic fields’ and not as ‘tone rows’ as they do not share the same ordering procedures associated with previous forms of twelve-tone music. McLeod reasons that twelve-tone rows “are conceived melodically and in which the order of the pitch classes [is] fixed as a series” whereas these twelve-tone harmonic fields “consist of four transpositions of a [triad], each of which may come in any order,” and furthermore, “the constituent pitch classes of each [triad] may also come in any order.”[17]

In her introduction to the English translation of Schat’s book, McLeod summarizes what it is about TCT that appealed to her:

I do find it particularly valuable as a point of reference, a sort of orientation-grid in an otherwise virtually uncharted sea of chromatic possibilities. But apart from that, what matters much more, are the principles that emerge here: the principle of deep-level harmonic symmetry; the concept of chromatic tonalities (in itself a stroke of genius) dependant on the chromatic triads (introducing the grouping principle, thence applicable to other groups of different sizes: intervals, tetrads, etc.); the principle of mobility – of the notes within the triad (or group), and the steering principle, the idea that different chromatic tonalities may generate one another. In these simple principles are enormous potential riches, for one can apply them in any direction one pleases […] to create a virtually endless number of new harmonic fields, mixed or otherwise.[18]

While TCT can be a complicated subject, especially when dealing with McLeod’s innovations, there are only five basic foundational concepts needed to understand Schat’s version of it, namely the chromatic triads, hours, the clock module, steering, and the resulting harmonic fields. A summary of these five components and their relationships can be expressed as follows: a chromatic triad representing one of twelve hour tonalities, which are organized around a clock module, can be steered to create the full non-repeating twelve-tone harmonic field that expresses that tonality.

EARLY THEORETICAL DEVELOPMENT

Tone-clock theory has its roots in a variety of 20^th century post-tonal theoretical techniques. As mentioned, its basis can be found in the dodecaphonic techniques of Schoenberg, as well as the atonal and early serialist works of the Second Viennese School, especially Webern’s serial derivation technique. Schat’s triads are identical to the trichords of Forte’s PC set theory, while the concept of steering is derived almost entirely from Boulez and his pitch-class set multiplication technique.[19]

It should be noted that neither of these derivations were intentional. While Schat’s “numbering and order of the triads are exactly the same as Forte’s […] [he] had no knowledge of or interest in set theory,”[20] and regarding steering, this was done subconsciously and Schat only realized it much later when McLeod pointed it out to him.[21] The hour fields themselves and their functionality behave very much like that of Messiaen’s modes,[22] as they can be employed freely without any of the restrictions commonly associated with serialist composition.

Although previous composers (Webern in particular) had segmented their twelve-tone rows into four similarly constructed trichordal PC sets, none had “developed a compositional system that could easily manipulate unordered trichords to derive other materials,” and Schat was determined to find a system that “would allow for the flexibility of unordered trichordal subsets within a twelve-tone composition while maintaining a coherent pitch-class relationship.”[23]

THE CHROMATIC TRIADS

The twelve chromatic triads provide the basis for each of the twelve chromatic tonalities. Forte identifies these triads in The Structure of Atonal Music, although his organizational system and terminology differs greatly from Schat’s and McLeod’s. Before delving into specifics, it is important to clarify some terminology regarding the chromatic triads. While these three-note shapes are conventionally referred to as ‘trichords’ in post-tonal analysis, following Forte’s labelling system, both Schat and McLeod favoured the term ‘triad’ instead, albeit each for different reasons. Schat, who made this discovery independent of Forte, came to his labelling system by arguing that “all triads […] can be formed from three different notes within the twelve-note octave” and that “the triad is a (tone-)spatial creation, whose character changes fundamentally if the mutual relationship between the constituent notes changes.”[24] McLeod’s reasoning was more of a direct challenge to Forte’s system, reasoning:

Since the term ‘dyad’ is often used to designate an interval, or group of 2 notes, I see no reason why the term ‘triad’ should not be extended to include any chromatic group of 3 notes, similarly ‘tetrad’ for a group of 4 notes, and so on (‘pentad’, ‘hexad’, ‘heptad’, ‘octad’, ‘nonad’, and ‘decad’), in preference to the ungainly and somewhat illogical ‘trichord’, ‘tetrachord’, ‘hexachord’, etc.[25]

In other writings on TCT, both ‘trichord’ or ‘triad’ have been used, depending on the author’s purpose and overall adherence to the theory.

A fundamental conceptual difference between these two systems is that, whereas Forte organizes his sets using PCs, labelling each note with a number that stands in relation to a fixed or moveable ‘doh’ (see figure 1), Schat uses ICs and groups his triads based on the intervallic distance between each pitch when placed in their most compact form, referred to as their intervallic prime form (IPF) by McLeod (see figure 2), which can be viewed as being synonymous with Forte’s ‘normal order,’ though not to be confused with his ‘prime form,’ which refers to a different principle. These intervallic distances are connected using a plus sign (+) in Schat’s system (ex: <4+3>), and a hyphen (-) in McLeod’s (ex: <4-3>). Schat’s method will be favoured in this article.

Figure 1: C major triad labelled in Forte’s PC set theory system

Figure 2: C major triad labelled in the classic tone-clock system

IPFs are especially important in TCT, as all the triads and their resulting harmonic fields must first be in this form before they can be put into musical application. It was McLeod who related Schat’s triads to Forte’s PC set theory and developed four criteria for determining if a triad is in its IPF:

1) the set must be in its most compact form;

2) the smallest interval comes first;

3) symmetrical forms are preferred over any asymmetrical forms; and

4) sets with fewest intervals are preferred[26]

No IPF triad will exceed the intervallic distance of a perfect 4^th (+5) between two pitches, as it will then become a rotation of another triad. This is also why there are only twelve chromatic triads to draw upon.

HOURS

Another integral part of TCT is the concept of ‘hours,’ each of which is representative of a chromatic tonality and is labelled by a Roman numeral. Every IPF triad is associated with a specific hour, and each of these hours has its own characteristic harmonic ‘flavour’ that relates to a familiar tonal sound (see figure 3).

Figure 3: The tone-clock hours in their IPF and corresponding harmonic ‘flavour’[27]

Of the twelve hour triads, seven are asymmetrical (hours II <1+2>, III <1+3>, IV <1+4>, V <1+5>, VII <2+3>, VIII <2+4>, and XI <3+4>), and five are symmetrical (hours I <1+1>, VI <2+2>, X <3+3>, XII <4+4>, and IX <2+5>),[28] which is determined by whether it contains one or two separate ICs. If an hour IPF contains two different IC integers, such as hour III for example which has an IPF of <1+3>, it is considered asymmetrical. Meanwhile, if the hour IPF has two integers with the same IC, such as hour VI <2+2>, it is considered symmetrical (see figure 4).

Figure 4: Example of asymmetrical hour III <1+3> and symmetrical hour VI <2+2> triads

Just as with tonal harmony, asymmetrical hour triads have a minor and major version, which is determined by the ordering of the ICs. If the smallest number comes first, it is minor, and the inversion would be major. In asymmetrical hours, the minor version is always the IPF.

McLeod developed the system for indicating the nature of these triads by simply labelling them with a lower case ‘m’ for minor, an upper case ‘M’ for major, and have neither for a symmetrical triad (see figure 5). Schat did not notate whether a triad was minor or major in his analyses, only its related Roman numeral hour. McLeod notes that “it was enough for him that the two were in the same hour.”[29]

Figure 5: Minor triad IIm <1+2> and major triad IIM <2+1> in IPF

THE CLOCK MODULE

Schat organized his triadic hours graphically around a clock module which appear clockwise in order of smallest IPF (1+1) to largest (4+4), labelling them with Roman numerals I-XII. Each hour is accompanied by a graphical representation of the entire harmonic field, which is derived by drawing the hour triad in its IPF and the corresponding three subset transpositions including the necessary transposed inversions (using the ‘steering principle’) required to complete the harmonic field (see figure 6).

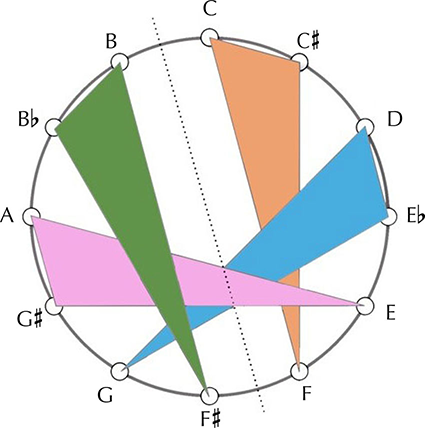
Figure 6: Triad IV <1+4> IPF and three transpositions on clock face[30]

When this process is applied to all twelve hours, it generates the twelve unique visual representations that produce the ‘Zodiac of the Hours’[31] (see figure 7)[32].

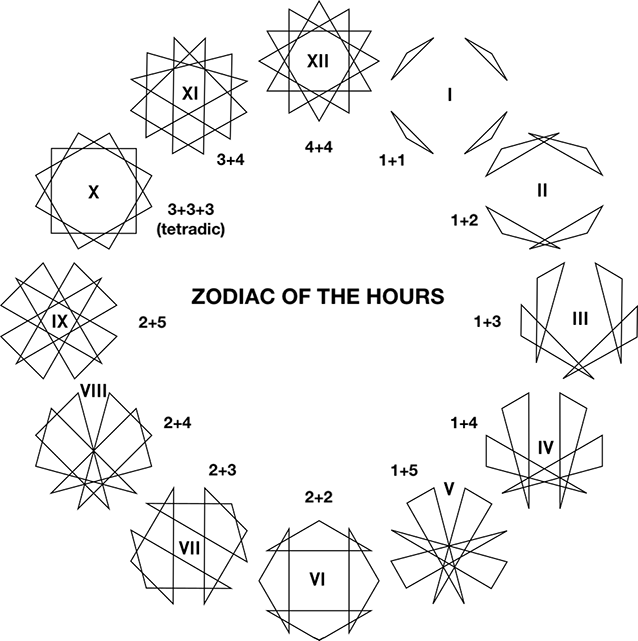
Figure 7: The Zodiac of the Hours[33]

STEERING

An essential component for generating the complete chromatic tonalities is an operation which Schat developed and identified as ‘the steering principle.’ This transpositional action directs, or ‘steers,’ one hour triad by another hour tetrad, both in IPF, to create the complete non-repeating twelve-tone harmonic field that defines a chromatic tonality. McLeod expands this concept beyond merely producing the pure hour tonalities and argued that this operation promotes unlimited growth in music since “any given note has the power to generate […] a group of notes”[34] and can be used to interpret and generate traditional tonal material. Consider, for example, a typical tonal I-IV-V progression in C Major. Within the context of TCT, these three major triads would be identified as belonging to hour XI <3+4> and are presented in their major form of <4+3>. The steering relationship between these three triads becomes clearer when they are ordered in perfect fourths (or five semitones) away from each other, with the dominant and subdominant triads encircling the tonic. These three hour XIM <4+3> triads are in fact steered by the symmetrical version of hour IX <5+5> to generate this familiar field, albeit ordered in their IPF form and not in a typical cadential pattern (see figure 8). The IPF of each individual triadic subset XIM <4+3> is labelled below, and the larger steering group of IX <5+5> is labelled above. The TCT notation for this figure is XIM/IX [G], which will be explained in more detail shortly.

Figure 8: A I-IV-V progression in C major presented as the tone-clock harmonic field XIM/IX [G]

This figure is representative of a typical TCT harmonic field figure. There are two notational variations used to demonstrate the steering relationships. In this version, which emphasizes the larger steering shape, the white notes represent the steering pitches, and the black, un-beamed notes are the embedded triads in their IPFs. In the other variation, which will be favoured in this article, beams separate each set within a larger beamed steering structure. In McLeod’s expansion, steering can also be used freely to create a harmonic field of any size, number of sets, and IC combinations.

TONE-CLOCK NOTATION

At this point, a brief explanation of TCT steering notation is required. Note how the example below is labelled as II/VIIIm⁴ [C] (see figure 9).

Figure 9: Full chromatic tonality of II/VIIIm⁴ [C]

The first Roman numeral refers to the hour being multiplied through transposition, or steered, the second is the steering hour, and the slash (/) separating them is the operational symbol for ‘steered by.’ The hour being steered, hour II, has an IPF of <1+2> and, as this is a representation of the harmonic field of a fully steered chromatic tonality of an asymmetrical hour, there must be a mix of both the minor and major versions to achieve the full non-repeating twelve-tone harmonic field. As both are used, the Roman numeral II is not followed by either an ‘m’ or ‘M,’ whereas steering hour VIII, being asymmetrical and presenting in one specific form, is followed by a lowercase ‘m’ to indicate it’s IPF of <2+4>. The superscript number after the Roman numeral refers to the size of this collection of steering pitches (known as an hour-group), in this case a 4, meaning tetrad. This could be applied to a larger-hour group of any size, such as a superscript 5 for pentad, or 6 for hexad. In the construction of these larger asymmetrical hour-groups, the numbers that make up the IPF alternate, so for example, a IIIm⁴ would be spelled out as <1+3+1>, while IIIm⁵ would be <1+3+1+3> and so forth. McLeod labels these as ‘Oedipus groups,’ “because they ‘limp along.’”[35] This is only one of a number of larger hour-group forms that McLeod identifies and utilizes in her compositions, which will be explained later. Finally, the PC set that the field originates from is stated in brackets, for example [C]. In this figure, the subsets of the full harmonic field are labelled A-D, as the identification of each set becomes important during both composition and analysis.

HOUR-GROUPS AND HARMONIC FIELDS

When a chromatic hour triad is expanded to a larger set, or even if that set has intervallic properties that are immediately identified as belonging to that hour, they fall into a general category which McLeod defines as ‘hour-groups.’ More specifically, an hour-group is “any intervallic form (intervals stacked, without note-repetitions) which can be interpreted as belonging within a single chromatic hour.”[36] One such hour-group of paramount importance to the generation of the chromatic tonalities is the expanded hour symmetrical tetrad (ST).

To generate a full chromatic hour tonality, one hour triad is steered by a ST version of another. Schat explains, “the relationship between the triads within the different tonalities (hours) can be expressed as tetrads from another tonality,”[37] effectively transposing the triad three times to produce the twelve-tone harmonic field: “a pitch-class set of modulo 12, from which a composer may freely manipulate not only the order of the ‘sub-fields,’ or constituent [triads], but also the order of the pitch classes contained within each [triadic] ‘sub-field.’”[38] For example, hour VI <2+2> is steered by tetrad Vm⁴ <1+5+1> to produce all twelve PCs (see figure 10). This is necessary to have all four separate triadic subsets that function as segments of the larger harmonic field.

Figure 10: Hour triad VI <2+2> steering by tetrad Vm⁴ <1+5+1>

In the above figure, hour VI <2+2> is a symmetrical hour and therefore has only one possible IPF. However, as mentioned previously, if one is to steer an asymmetrical hour, such as hour III <1+3>, one must have an even distribution of both minor and major triads to generate the complete tonality. The ordering of the minor and major triads follows no consistent pattern across the hours and is unique to each steering, though there must be two instances of both qualities to retain symmetry. For example, in III/VIIm⁴ the harmonic field follows an (m,m,M,M) sequence, meaning that subsets A and B are minor, while subsets C and D are major. However, in hour V <1+5> steered by hour IIM⁴ <2+1+2> the ordering is an alternating (m,M,m,M) making subsets A and C minor, and subsets B and D major (see figure 11). There are only four possible variations of this pattern, the two mentioned previously and additionally (M,m,M,m), and (M,M,m,m).[39]

Figure 11: Example of different triadic quality ordering in fields III/VIIm⁴ and V/IIM⁴

The number of steering possibilities to generate the complete tonality will vary across hours. For example, while hour II <1+2> has only one possible steering of hour VIIIm⁴ <2+4+2>, hour VIII <2+4> has four potential steerings, namely hours IIIm⁴ <1+3+1>, IIIM⁴ <3+1+3>, IVM⁴ <4+1+4>, and XIM⁴ <4+3+4>, with each variation having a possible twelve transpositions (see figure 12).

Figure 12: All possible steerings of hour VIII <2+4> chromatic tonality

In total, Schat identified a total of twenty possible steerings for the full tone-clock with McLeod expanding the list to twenty-eight (see table 1), each yielding a field that has either three, six, or the twelve transpositions, except for hour XII <4+4>, which has zero transpositions. Just as with the hour triads, these fields must be presented in their IPF.

Table 1: Table of all tone-clock hour chromatic tonalities and their steerings

There is one anomaly in Schat’s system, and that is the case of hour X <3+3>, a natural diminished triad in tonal harmony. It is impossible to create a four-set triadic harmonic field in this hour, therefore Schat’s solution was to make an exception and have this chromatic tonality present as three hour X⁴ <3+3+3> tetrads steered by an hour I <1+1> triad (see figure 13).

Figure 13: Full steering of hour X <3+3> as a tetradic X⁴/I [C]

Excluding the tetradic hour X <3+3>, there are twenty-seven possible steerings to achieve the full harmonic fields of the remaining eleven triadic chromatic tonalities. When accounting for all possible transpositions, this yields a total of 176 variations (see figure 14).

Figure 14: Twelve-note triadic tone-clock tonalities (in stave notation from [C])[40]

As some of the hour tonalities share the same steering hour, these ICs can be used as pivot points to ‘modulate’ between related chromatic tonalities through their shared steering PCs. For example, both hour II <1+2> and hour VII <2+3> share the common steering of hour VIIIm⁴ <2+4+2> (see figure 15).

Figure 15: ‘Modulation’ of hours II <1+2> and VII <2+3> by VIIIm⁴ steering

DEEP-LEVEL STEERING

Thus far, all steering examples have been cases of ‘surface-level’ steering. However, as any PC or IC set can generate new material by functioning as a steering point, this opens the door to multiple levels of steering, known as ‘deep-level’ steering. This process is used to preserve relationships of the various steering levels, while also allowing the composer greater creative flexibility to organize a piece at multiple structural levels. This means that the steering principle is not only used to generate a twelve-tone harmonic field, but also a network of interrelated material that can support a larger work. This allows for multiple transpositions of subset fields within a single larger steering structure.

Consider the following example, where the hour II triad <1+2> is steered by its native symmetrical tetrad VIIIm⁴ <2+4+2>, which then becomes a superset that undergoes a deeper-level steering along hour IIIM <3+1>, resulting in three transpositions of the initial hour II <1+2> harmonic field. This would be notated by adding an additional steering symbol and the deep-level steering IC, presenting in this case as II/VIIIm⁴/IIIM (see figure 16).

Figure 16: Deep-level steering field of II/VIIIm⁴/IIIM [C]

The above example has three levels at play:

1. The surface-level steering which provides the basis for the example is generated from hour II<1+2/2+1> steered by hour VIIIm⁴ <2+4+2> (see figure 17a).

2. The second level of steering of VIIIm⁴ <2+4+2> by IIIM <3+1> (see figure 17b).

3. The third, or in this instance, the ‘deep-level steering hour’ of IIIM <3+1> (see figure 17c).

Figure 17a: Surface-level steering of II/VIIIm⁴ [C]

Figure 17b: Second-level steering of VIIIm⁴/IIIM [C]

Figure 17c: Deep-level steering hour IIIM <3+1> [C]

This process can continue for as long as the composer wishes to achieve the desired musical result.

McLeod later expanded the use of steering by positing that any hour-group of any size (or any IC set for that matter regardless of content) could be steered by another without any consideration for repeated pitches or if all twelve PCs are even present. This implies that “the groups and sub-groups involved may be of any size, and the level of ‘unordered-ness’ of freedom of movement within a group and subgroups may be of any degree desired.”[41]

This concludes the overview of the basic principles and operations within Schat’s version of TCT. McLeod’s expansion of his basic premise (i. e.: hour triad steered by hour tetrad = complete harmonic field of a chromatic tonality) is considerable, and while there is certainly not enough space to properly address all her ideas in this paper, a few key concepts will be examined.

TONE-CLOCK THEORY’S EXPANSION

The first key conceptual difference between Schat’s ‘classic’ TCT and McLeod’s expansion is that, whereas Schat primarily conceived of it as a tool for generating the full non-repeating twelve-tone fields as material for his compositions, McLeod embraced the principle that “anything can steer anything,”[42] opening it up to a larger realm of harmonic possibilities. This allowed McLeod to reframe all of Forte’s PC sets as IC sets in their IPFs and analyze them according to their intervallic makeup and relationship to the chromatic tonalities, identifying structural properties and interwoven connections that Forte did not, leading to the categorization of larger hour-group fields of up to ten PCs, as well as the creation of a concise labelling system for asymmetrical groups that have more than two ICs and are not considered hour-groups. Additionally, she developed various transformational methodologies to build new chromatic networks, discovering new relationships between the PC sets that are only apparent through this intervallic framework. Creatively, this led to new compositional techniques which she refined during the process of writing her 24 Tone Clock Pieces for piano.

EXPANDED NOTATIONAL PRACTICES

Both Schat and McLeod consistently apply a similar system for notating the triadic hour tonalities, but when dealing with fields that cannot be easily categorized as such, their approaches for labelling become very different. For one thing, Schat was less precise in his notation, as he did not distinguish between major or minor triads and did not give the starting PC of his fields. Also, while both composers conceived of pitch collections that contained more than two ICs as a “combination of smaller hour-groups,”[43] Schat always prioritized Roman numerals while McLeod would simply notate the ICs in bold numbers. Furthermore, another vital addition by McLeod that both Schat and Forte overlooked was to indicate the starting PC of the figure by including it within brackets, such as [C], or using the Forte PC number within a moveable ‘doh’ system when just giving the overall shape for easy transposition, such as [0]. This simple addition is a key development that provides a more complete picture of the intervallic shape being discussed and greater ease in transposition and creative application.

The divergence between these two approaches has resulted in differing methodologies of TCT analysis, usually dependent on whether the theorist’s approach is based on either Schat’s or McLeod’s and is sometimes made even more confusing by attempts to fold TCT into another theoretical discipline, such as PC set theory, which is not always a compatible match. Examples of both methods will be given, though McLeod’s will ultimately be favored.

ASYMMETRICAL TETRADS AND SYMMETRICAL PENTADS

One example of such a discrepancy would be an asymmetrical tetrad (AT), wherein the ICs do not correspond to a direct Roman numeral hour labelling. In keeping with Schat’s method of viewing everything through this lens, the ‘classic’ TCT approach would be to view an AT as two combined triads that must be built from a shared IC which acts as pivot point, such as in the case of hours IV <1+4> and VIII <2+4> which share an IC of 4 and can therefore be combined. In Schat’s approach, the resulting tetrad would be labelled as a combination of Roman numerals IV+VIII <1+4+2> or as VIII+IV <2+4+1> depending on the ordering of the ICs. To clarify this further, Canadian theorist Erik Fernandez Ibarz proposed the addition of the symbol ‘AT’ before the numerals (see figure 18).

Figure 18: Asymmetrical tetrads ATIV+VIII <1+4+2> and ATVIII+IV <2+4+1>

Conversely, McLeod would notate these two collections simply as an IC set with the use of bold numbers. Therefore, ATIV+VIII would instead be labelled as 142, and ATVIII+IV as 241.

McLeod keeps the Roman numeral labelling when dealing with symmetrical pentads (SP), identifying this as an important hour-group that deserves shorthand notation. Just as with an ST, an SP consists of an intervallic palindrome where a triad’s ICs are inverted and can be expressed in either its major or minor form (see figure 19).

Figure 19: Symmetrical pentads SPVIIm <2332> and SPVIIM <3223> [C]

Schat’s insistence that all tone-clock fields must generate all twelve PC’s, keeping with his concept of TCT as a tool for twelve-tone composition and that it be expressed exclusively using Roman numerals, runs into major problems when dealing with pitch collections that do not correspond directly to a chromatic tonality. He attempts to solve this issue with the concept of ‘composite tonalities,’ wherein one could combine multiple hours through a shared or mixed steering tetrad to form a greater variety of twelve-tone fields, though notating this with Roman numerals quickly becomes unwieldly and imprecise. Furthermore, his focus on full twelve-tone collections omits a large selection of chromatic possibilities. McLeod’s abandoning of these limitations and replacement of the Roman numerals with bolded IC integers solves this issue, allowing for free movement within all of chromaticism. This led to the cataloguing of collections known as larger hour-groups that, while related to a given chromatic tonality, do not follow Schat’s established steering patterns and are not easily expressible using Roman numerals.

LARGER HOUR GROUPS

Larger hour-groups are more complex collections of ICs that are still clearly identifiable as belonging to a specific chromatic tonality. It is also important to note here that some of these collections expand past the octave limit, and function as a specific ordering of a pitch-class set to achieve a particular harmonic character and could be presented also in their IPF. In fact, some of these groups will even include repeated pitches to fully follow their pattern, such as hour VII <2+3> for example, which when fully expanded to the point of complete repetition will have two instances of each pitch. McLeod distinguishes most of these groups by their size, hour, intervallic structure, major or minor when applicable, and as symmetrical or asymmetrical. It is at this point in the system where she largely leaves Schat’s Roman numeral-based approach behind in favor of her intervallic labelling methodology as she felt that “fancy roman names […] for every possible form of hour-group [would] only confuse the issue.”[44] The exception to this is the case of expanded ‘Oedipus’ groups, which as mentioned earlier, McLeod would categorize as the expansion of an asymmetrical hour beyond a triad wherein the ICs follow an alternating pattern.

These ‘Oedipus’ groups can continue to generate larger hour-groups up until the IC sequence repeats itself, which is different for each hour. For example, an hour II <1+2> Oedipus group can be expanded to a maximum of eight PCs, while hour III <1+3> has only six (see figure 20). McLeod referred to these completely expanded hour complements as “full-grown hourly tonalities.”[45]

Figure 20: ‘Full-grown hourly tonalities’ of hour-groups IIm⁸, IIM⁸, IIIm⁶, and IIIM⁶ [C]

While none of the other examples of larger hour-groups are expressed with Roman numerals, McLeod does however categorize four distinctive symmetrical hour-group configurations which she identifies as “‘Gemini’ groups, the ‘greater Geminis,’ the ‘Gemini triplets,’ and the ‘Oedipus twins’ respectively.”[46] As these larger hour-groups can be conceived of as a combination of two or three smaller sets, repeated pitches are allowed, and the intervallic consistency is prioritized. Each follows their own pattern that can be applied to any asymmetrical hour tonality. In table 2, the given ICs are in hour II <1+2> to demonstrate how these patterns change, and these are translated into stave notation in figure 21 below.

Table 2: Larger hour-group formations in hour II <1+2>

Figure 21: Hour II <1+2> larger hour-groups in stave notation

Thus far, all the examples given have been hour specific. As this can be potentially limiting from the standpoint of harmonic diversity in one’s music and doesn’t account for many basic shapes within tonal music, it is of course necessary to expand the scope of TCT to beyond just the chromatic tonalities. While Schat tried to rectify this with his concept of ‘composite tonalities,’ ultimately it is McLeod’s more flexible approach of allowing for the steering of a collection of any size or intervallic shape by another that allows for these harmonic possibilities and is a key aspect of her expansion.

MCLEOD’S CHROMATIC MAPS

McLeod’s book, Tone Clock Theory Expanded: Chromatic Maps I & II, which is primarily a reframing of Forte’s The Structure of Atonal Music, provides comprehensive entries on every one of his PC sets through two separate charts; Chromatic Map 1: IPF Chart and Chromatic Map 2: Array Steering (AS) Chart. In both, McLeod uses Forte’s PC set names to organize her entries and includes some of the same information while providing additional insights absent from Forte’s book. Her impetus for creating these maps was driven by her position that Forte’s prime forms fail to properly consider “the structural properties of the groups, which are really what distinguish one group from another in the mind a musician.”[47] For example, while Forte’s entries include the interval vector, telling us how many instances of each interval occurs in a set, it does not tell us where they occur, making them perhaps mathematically useful for a theorist, but “unsatisfactory to work with practically,”[48] while McLeod’s AS map solves that issue. By combining Schat’s chromatic triads with her own intervallic labelling system, McLeod provides the reader with a comprehensive view of all possible intervallic possibilities within a given PC set that can easily be translated into stave notation. Ultimately, McLeod’s goal was to offer a comprehensive overview of the entire chromatic system that was simplified, economical, and most importantly, practically useful in creative application, especially as she found set theory to be “unreadable to most [composers].”[49]

Chromatic Map 1, the IPF Chart, provides detailed entries on each PC set and identifies any connections it has to tone-clock specific sets and pre-existing harmonic systems. It is organized in row entries with each column denoting a separate aspect of the PC set, such as any existing name for the collection or subscale relationship it may have, its IPF, its TCT names if applicable, any other identities it may have, an interval array, hour triad array, its chromatic complement, and its mode subset (referring to Messiaen’s modes of limited transposition). She will also note if it has a relationship to an established shape from another post-tonal theorist, such as one of Babbit’s all combinatorial hexads, or Xenakis’ sieve theory. While this information is obviously beneficial for analysis, it is also practically useful for composition, as it lays out clear relationships between one PC set to others and lists the possible forms it can take (see figure 22).

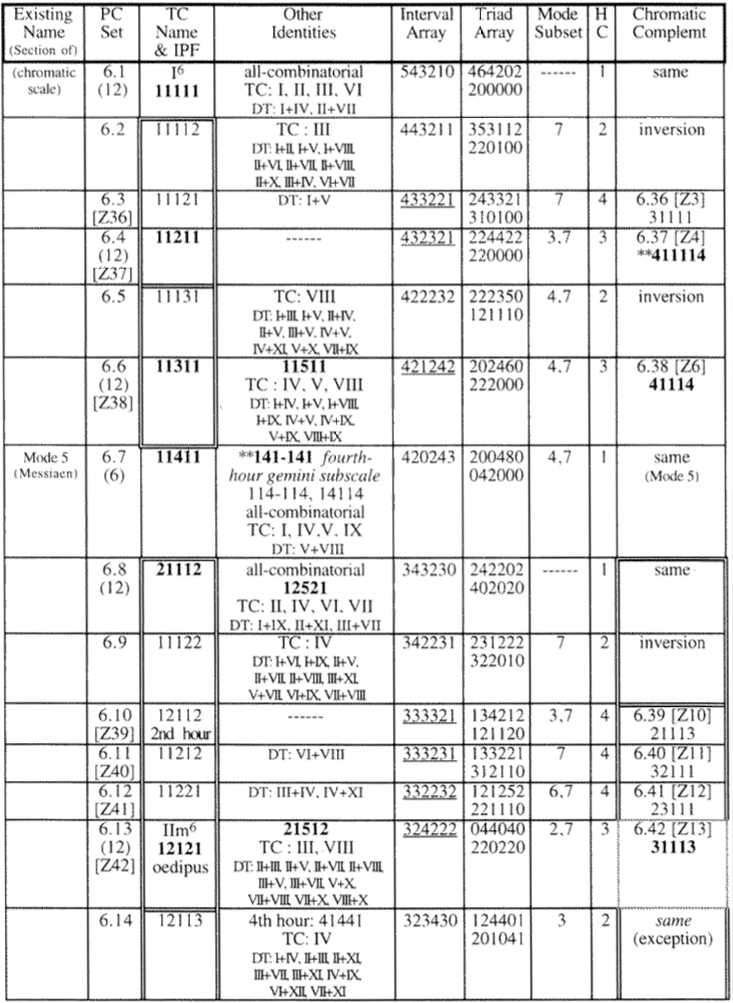
Figure 22: Example of Chromatic Map I (IPF Chart)[50]

Chromatic Map 2, the AS Chart, is particularly useful for creative application, because as just mentioned, it provides the exact location of each intervallic or hour triad subset located within a given PC set, using only the tone-clock notation that has been discussed previously (see figure 23).

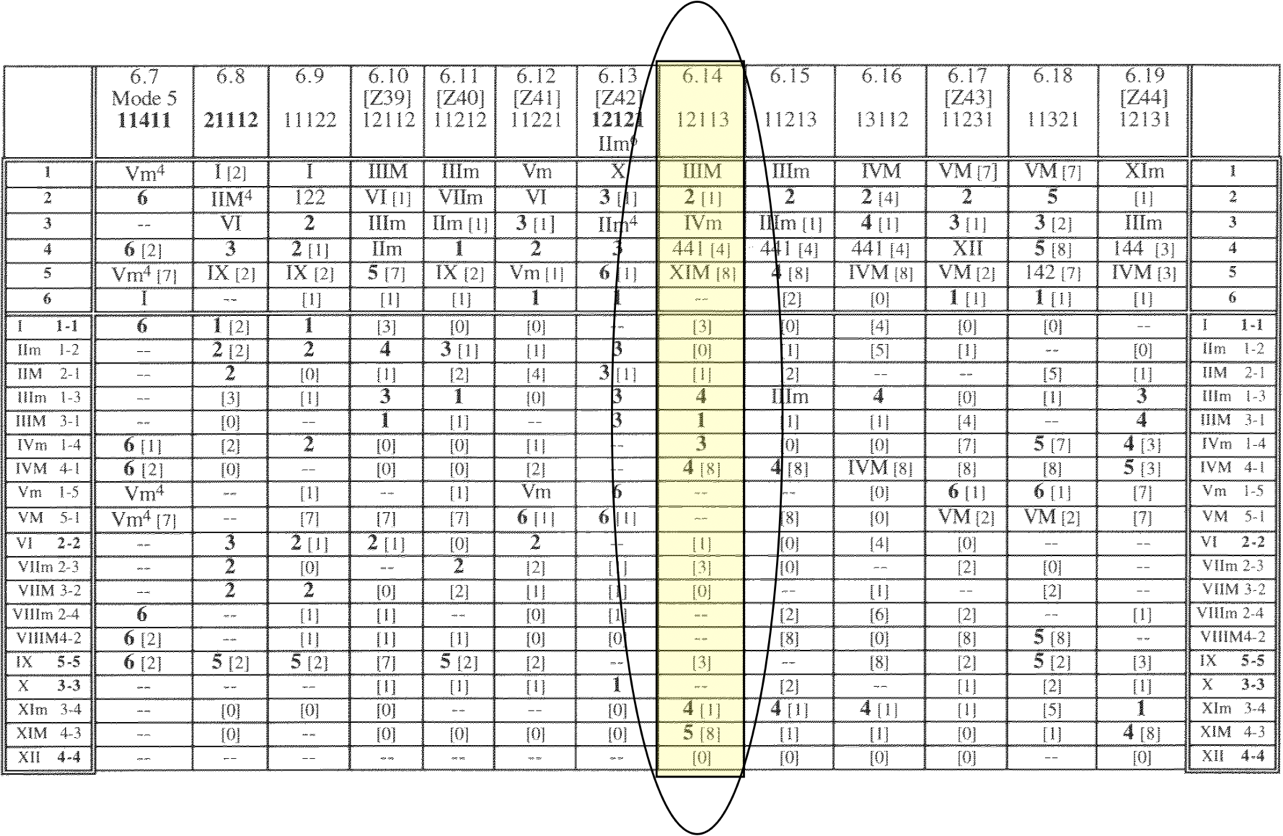
Figure 23: Entry for PC set 6.14 from Chromatic Map 2 (Array Steering Chart)[51]

In this chart, the PC sets, which are each labelled by their IPF, are organized in columns, and are divided into two sections: the interval array and the triad array. The top 6 rows are the interval array and show where each individual instance of intervals 1–6 (semitone to a tritone) can be found in the overall PC set. The second section shows every instance of an hour triad that can be generated within the sets. The entries themselves are indicative of the steering IPF that will generate these fields. For example, the highlighted entry 6.14 from figure 24 lists IIIM for IC 1. That translates to their being a dyadic field of two PCs separated by a semitone occurring along a steering pattern of <3+1> from pitch [0]. The entry below it for IC 2 (a whole tone) has the symbol 2 [1], meaning the steering set contains only two PCs separated by a whole tone, and the bracketed [1] indicates where the pattern originates from in that PC set, or from [D] if [0] equals [C]. The entry for IC 4 reads 441 [4], showing an IC set that cannot be notated with just a Roman numeral so she uses her intervallic labelling system. The bracketed [4], as before, indicates that PC starting point for the IC set. If [0] is assumed to be [C], then beginning from PC [4] (or [E] in this transposition), a steering field of [E, G, C, D] is generated for the dyadic subset of IC 4. In the triad array section of this chart there are entries that contain only a bracketed PC number, such as the entry for hour I <1+1>, meaning that there is only one instance of that chromatic triad within the PC set and it occurs from PC [1] (or [C]). Finally, entries with two dashes [--] simply indicate that the IC class is not present within a PC set. With a good understanding of this notational system, this entry is easily translated into stave notation (see figure 24).

Figure 24: Array Steering chart entry for PC set 6.14 in stave notation from C [0]

In working with her expanded concept of TCT, McLeod was able to discover many other relationships between the chromatic tonalities and individual PC sets that can only be perceived and properly analyzed through this framework. This led to the development of numerous other harmonic networks including ‘anchor-forms,’ ‘anchor remainders,’ ‘multiple-nature hour-groups,’ ‘intrinsic spin networks,’ and ‘binding networks,’ which in turn led her to innovative new compositional techniques. The material on these topics is substantial and must be reserved for a separate article.

CRITICISMS OF TONE-CLOCK THEORY

When Schat first published his treatise, it was met with substantial skepticism from both his compositional peers and the theoretical establishment, despite it being tested and verified by composer and theorist Rokus de Groot through a series of articles in the Dutch musicological journal Key Notes. McLeod also faced pushback from her community, such as while receiving praise for her 24 Tone Clock Pieces from her former teacher New Zealand composer Douglas Lilburn, he added that he “hoped they weren’t anything to do with ‘that system.’”[52] Due to Schat’s status as an already controversial ‘activist/composer,’ he has received the bulk of the criticism, and not always undeservedly due to some of the inherent limitations and problems of his ‘classic’ TCT which are mentioned above. In a review of the English reprinting of The Tone Clock for Tempo magazine, critic Malcom Miller points out that “the restriction to triads is itself artificial and unnecessary” and notes that “Schat’s chromatic universe nevertheless falls short of symbolizing a harmonic Utopia” but is rather a “partial glimpse into a far richer universe of possibility.”[53]

Another harsh review of Schat’s work came from musicologist Richard Toop who wrote that “Peter Schat’s ‘tone-clock,’ which in my opinion produced one nice piece - Canto General - and then nothing of more than parochial interest.”[54] Likewise, composer Morten Feldman was openly critical of the system to Schat’s face during a symposium in Darmstadt on tonality in 1984 when, in an argument during a public forum, he insisted that “you need a more matching relationship between pitch, timbre, register, instrument […] I can’t write a note unless I know its instrumentation, its register, its shape in context, and neither should you.”[55] This lack of ‘global’ considerations can be a problem for many composers looking for inspiration from a new system, though it should be noted that both Schat and McLeod hint at potential rhythmic applications of TCT, but do not elaborate on that point.

Dutch saxophonist and composer Dick de Graaf mentions a major rhythmic problem built into this system, namely its “three-ness, or more precisely: the predominant presence of three-note groupings”[56] in his 2017 Doctoral thesis Beyond Borders: Broadening the Artistic Palette of (composing) Improvisers in Jazz. A major part of his thesis concerns the application of TCT to jazz improvisation and composition, and his focus is on the work of American saxophonist John O’Gallagher who introduced Schat’s theoretical principles to the jazz community through his book Twelve Tone Improvisations: A Method for using Tone Rows in Jazz (2013), (though not as TCT, as he prefers to simply identify the ‘rows’ using their IC classes rather than with Roman numerals and makes only brief references to the theory itself). Like Schat, O’Gallagher is primarily concerned with the chromatic triads, which he refers to as trichords, and their ability to generate the full harmonic fields of the chromatic tonalities, which he just refers to as twelve-tone rows. Consequently, the criticisms Schat received from Miller regarding his obsession with the triads can also apply to O’Gallagher’s jazz approach. De Graaf goes on to suggest some rhythmic solutions and even brings up the work of Dutch composer and organist Gerrit de Marez Oyens who “came up with the idea to divide the Tone Clock’s twelve rows into three tetrachord segments,”[57] rearranging the chromatic tonalities into three sets of four PCs, which is certainly possible in some cases, but not all.

McLeod herself noted many of these shortcomings and viewed them as a byproduct of Schat’s insistence on following his own “strict tone clock rules” which led to “absolutist thinking”[58] that ultimately limited him creatively. Schat in fact was “extremely surprised” by McLeod’s music, asking her in a letter “how do you use it so freely?!”[59] Her expansion sought to address many of these problems, and the argument can be made that she was successful, as her version of TCT is far more comprehensive than his. Wide-spread dissemination of TCT also remains an issue. The greatest challenges with bringing TCT into greater usage and awareness stem largely from a) the lack of research on the subject, b) the differing methodologies for terminology, notation, and analysis, and c) that pedagogical approaches for teaching it as either an analytical framework, a compositional tool, or as a basis for jazz improvisation are either in very early stages of development or non-existent.

PRACTICAL APPLICATION IN CONTEMPORARY MUSIC AND JAZZ

Examples of TCT’s creative application are still largely limited to the works of Schat and McLeod, though its reach and influence has slowly increased. McLeod’s 24 Tone Clock Pieces for piano remains one of the most accessible and influential series of compositions using this system, while everything Schat composed from the early 1980’s until the end of his life can also be categorized as a tone-clock work, such as Genen, Op. 47 (2000), De Hemel, Op. 37 (1990), and his opera Symposium (1988).[60] An essential aspect of TCT’s practical application, as opposed to previous forms of twelve-tone or serialist composition, is that there is a complete freedom of ordering and use of repeated pitches. While both McLeod and Schat organize the harmonic material in their compositions to make the individual sets obvious, this is not mandatory and can function exclusively as an organizational tool for the composer. Schat writes at length on his website about how he had conceived of TCT as a reaction to serialist compositional methodologies which he found to be “unmusical.”[61]

Interestingly, while there are only a handful of contemporary classical composers who have openly worked with TCT, such as New Zealand composers Leila Adu-Gilmore or Michael Norris, it has largely been taken up by jazz musicians. McLeod herself felt that this was a natural evolution for this system, writing in her introduction to the English reprinting of The Tone Clock that she could “see it as an avenue for the more adventurous jazz spirits as well, one or two of whom indeed are not so far from it even now.”[62]

There exists in the Netherlands a tradition of applying TCT concepts to jazz improvisation dating back to the late 90’s through the early experimentations of Dutch bassist Theo Hoogstins, and it has recently been championed by saxophonist Jasper Blom, who even released a tone-clock-based tribute record to Schat entitled Polyphony 3 (2023). Outside of the Dutch jazz scene, the most influential practitioner of tone-clock improvisation and composition is John O’Gallagher, who while teaching at the Birmingham Conservatoire in the UK had a direct impact on fostering this approach amongst young musicians in the UK jazz scene, and whose book has influenced improvisers around the world.[63]

CONCLUSION AND FUTURE RESEARCH

The primary purpose of this paper is to give an overview of TCT, its history and theoretical mechanics, as well as to provide an explanation of its notational system and terminology in the hope of stimulating an interest among composers and researchers. A further purpose is to stress the value of Jenny McLeod’s expansions in the discourse of TCT, as she is often omitted in articles in favor of Peter Schat. While this is largely understandable since her book Tone Clock Theory Expanded: Chromatic Maps I & II was never officially published, her contributions to TCT are substantial and need to be recognized. This is a considerable task and deserves to be addressed separately in future articles.

Nevertheless, this article barely scratches the surface of TCT’s creative applications in both contemporary classical composition and in jazz. Currently TCT remains a largely obscure and under-researched subject, though that is changing. In fact, more has been written about TCT in the last decade than the previous 30 years, and while it is still a small, developing field with diasporic bases in Europe, New Zealand, and North America, each with its own terminology and usage, it is undeniable that TCT is growing in influence and application. Theorists, composers, and jazz improvisors around the world, increasingly from a younger generation, are adopting TCT into their creative and academic work to the point where it is now imperative that a coherent terminology along with consistent educational sources understandable to non-academic musicians be created and disseminated. Ultimately, this rich and growing field deserves serious consideration and study by practicing musicians as well as academics.

Finally, it should be stressed that in addition to its numerous applications to composition and improvisation, TCT offers post-tonal theorists a new methodology for analysis which promises unique insights beyond that of Forte’s PC set theory and paves a vast avenue of research ripe for exploration. However, it is important to remember that TCT is not meant to replace, but rather expand upon, pre-existing creative and analytical practices. It offers a new framework for musical thought and a map of the complete chromatic realm, the purpose of which is first and foremost to function as a tool for making and understanding music. Its utility will become more evident as composers and improvisers continue to develop it further through their own creative work. As Schat wrote: “The tone clock theory can only be judged when it’s heard!”[64]