… einen inhalt bekam mein leben erst als ich ernsthaft mich auf die musik zu konzentrieren begann […] – dabei war ich ganz auf mich allein gestellt…[1] (Hugo Kauder)

1. Vorarbeiten und -überlegungen

Die Aufarbeitung von Hugo Kauders Leben und seinem kompositorischen wie musiktheoretischen Werk stellt in weiten Teilen nach wie vor ein Forschungsdesiderat dar. Gerold Gruber, Leiter des »Exilarte Zentrums für verfolgte Musik« der Universität für Musik und darstellende Kunst Wien, formuliert es in Anlehnung an Stefan Zweig wohl am treffendsten:

Hugo Kauder gehört gleichfalls dieser Generation an, welche zum Verstummen gebracht wurde, ›losgelöst von allen Wurzeln und selbst von der Erde, die diese Wurzeln nährte‹ (Stefan Zweig, Die Welt von Gestern).[2]

Einen Meilenstein in der Erforschung von Hugo Kauders Leben setzte Karin Wagner 2018 mit der Biographie Hugo Kauder (1888–1972): Komponist – Musikphilosoph – Theoretiker. Diese Arbeit dient als Grundlage für weitere Detailforschungen, auch bezüglich Kauders musiktheoretischen Schaffens. Der Entwurf einer neuen Melodie- und Harmonielehre (1932) ist gedanklich in den musik- und naturphilosophischen Diskurs der 1920er Jahre über das Kosmische oder Göttliche der Musik einzuordnen, worauf später genauer Bezug genommen wird.

Im Folgenden werden nach einer Kontextualisierung und Darstellung der Ziele und wichtigsten Inhalte von Kauders Entwurf einer neuen Melodie- und Harmonielehre seine musiktheoretischen Konzepte anhand einer Melodieanalyse der Kleinen Suite für Bratsche allein (1926) konkretisiert. Das Ziel dieser musikalischen Analyse liegt in der Reflexion von Kauders musiktheoretischen Anschauungen – die er wenige Jahre nach der Komposition schriftlich dargelegt hat. Kauder blieb dabei, seine Schrift als »Entwurf« zu bezeichnen – ein Hinweis auf Unvollendetes, Fragmentartiges, Aphoristisches, Bescheidenheit oder eine Eingliederung in einen aktuellen (daher noch nicht vollendeten) Diskurs?

Neben Fragen der Kontextualisierung geht es um das Sichtbarmachen der Musiktheorie Kauders, um sie schließlich in Fachkreisen zur Diskussion stellen und als Ausschnitt aus der Geschichte der Musiktheorie im frühen 20. Jahrhundert begreifen zu können.

Das Hauptmaterial der vorliegenden Studie besteht aus:

Kauder, Hugo (1926), Kleine Suite für Bratsche allein, Wien / New York: Universal Edition.

Kauder, Hugo (1932), Entwurf einer neuen Melodie- und Harmonielehre, Wien: Universal Edition.

2. Analyse und Kontextualisierung von Kauders Melodie- und Harmonielehre

Kauders Entwurf einer neuen Melodie- und Harmonielehre ist das Ergebnis seiner in den 1920er Jahren entwickelten, an die griechische Tetrachordlehre angelehnten Skalentheorie.[3] Sein primäres Ziel ist die Darstellung einer Lehre, mit deren Hilfe sich eine auf »allezeit gültigen geistigen Gesetzen« beruhende Musik komponieren lasse.[4] Anhand der hergeleiteten Skalen und Tetrachorde bildet Kauder in weiterer Folge Akkorde und Akkordverbindungen. Vorauszuschicken ist, dass sich Kauder prinzipiell auf diatonische Skalen beschränkt.

2.1. Einflüsse und Kontexte: Rudolf Pannwitz, Egon Lustgarten, Arthur von Oettingen, Hugo Riemann, Paul Hindemith, Arnold Schönberg

Kauder ordnet sich bereits im Vorwort seiner Schrift einer bestimmten musikphilosophischen Denkrichtung zu. Widmungsträger der Schrift ist Rudolf Pannwitz, über den Kauder im ersten Absatz des Vorwortes schreibt:

Die vorliegende kleine Schrift ist veranlasst durch Rudolf Pannwitz’ ›Renaissance der Vokalmusik aus dem Geiste und als Schöpfung des Kosmos Atheos‹. In diesem Werke wird die geistige Welt der Musik neu aufgebaut und damit der Grund gelegt zu einer Erneuerung der Musik selbst, indem ihr wiedergegeben wird, was sie im Altertum ganz, im Mittelalter noch in halbverstandenen Resten besessen, nun aber seit Jahrhunderten ganz verloren hat: eine auf geistigen Grundtatsachen beruhende Lehre. Diese weiter zu entwickeln und für die unmittelbare Kunstübung fruchtbar zu machen, wird in dem folgenden Entwurf einer neuen Musiklehre versucht.[5]

Rudolf Pannwitz (1881–1969) setzte sich als Philosoph, Schriftsteller und Dichter insbesondere mit dem Werk Nietzsches auseinander. Zu Pannwitz’ wichtigsten Schriften zählen Die Krisis der europaeischen Kultur (= Die Freiheit des Menschen, Bd. 1, 1917) und Kosmos Atheos (= Die Freiheit des Menschen, Bd. 3, 1926). Auf zweitgenannte Schrift bezieht sich Kauder konkret in seinem Vorwort der Melodie- und Harmonielehre.[6] Ein reicher Briefwechsel dokumentiert den musikphilosophischen und persönlichen Austausch zwischen Kauder und Pannwitz. Für weiteres Hintergrundwissen zu Nieztsche und Pannwitz sei auf László V. Szabós Beitrag »Der kosmische Übermensch. Zu Nietzsches Wirkung auf Rudolf Pannwitz« verwiesen.[7]

Im Hinblick auf die Frage nach den Voraussetzungen für Kauders Schrift ist neben der Freundschaft mit Pannwitz auch jene mit Egon Lustgarten (1887–1961) zu nennen. Lustgarten und Kauder verband »nicht nur das Interesse an musikhistorischem Quellenmaterial, sondern auch die Vision, Musik und Metaphysik in Synthese zu bringen und teleologisches Denken auf die Musik zu übertragen.«[8]

Lustgarten, ein österreichischer Dirigent, Pianist und Komponist, folgte 1921 dem Ruf als Professor für Theorie und Komposition an das Neue Wiener Konservatorium. In den beiden Jahren zuvor veröffentlichte er seine musikphilosophischen Ansichten in den Musikblättern des Anbruch.[9] »Als Quintessenz schrieb Lustgarten der Musik, diesem ›Spiegel der Weltwerdung aus dem Chaos‹, eine Bindung an das ›göttliche Prinzip‹ zu.«[10] Ähnliche Ansichten vertrat auch Kauder in seinen im Jahr darauf in den Musikblättern des Anbruch veröffentlichten Beiträgen, in denen er sich explizit auf philosophische Ideen Friedrich Wilhelm Joseph Schellings beruft.[11] Später steuerte Kauder zu seinen theoretischen Überlegungen auch »die adäquate Musik bei und kommentierte die philosophischen Positionen kompositorisch bzw. die kompositorischen Positionen philosophisch.«[12]

Konkret ist dieses musikteleologische Gedankengut (Musik ist auf eine »höhere Ordnung« hin ausgerichtet und soll diese abbilden) in Kauders Melodie- und Harmonielehre anhand seiner Ausführungen zu den Grundbedingungen der Töne und Tonverhältnisse zu erkennen. Die Zahl begreift Kauder als »schöpferisches Prinzip« und alle Tonverhältnisse als »tönende Realisation von Zahlenbeziehungen«. Auf den Grundzahlen zwei, drei, vier und fünf und ihren jeweiligen Vielfachen beruhe die »göttliche Ordnung der Dinge«.[13] In diesem Zusammenhang spricht Kauder außerdem von einem »Vollkommenheitstrieb des menschlichen Bewusstseins«, der sich in einem Streben nach »vollkommenen Formen« äußere.[14] Das Irrationale sei zwar in der Kunst vorhanden, aber dem Rationalen untergeordnet, »denn nur dieses vermag eine geistige Grundlage zu geben, Gesetz und Ordnung zu schaffen eine Welt aufzubauen.«[15]

Ein Querverweis zu Gustav Mahlers Ideen der Abbildung der Welt durch seine Symphonien liegt auf der Hand. Kauders Vorliebe für dessen Musik schwingt nicht zuletzt in seinen Beiträgen »Vom Geiste der Mahlerschen Musik« und »Die Instrumentation Mahlers« mit.[16]

Für Kauder entspringt das Rationale der Musik einer naturgegebenen Ordnung, die sich in der Ober- und Untertonreihe fassen lässt.

In der antiken Musik sind alle Skalen in fallender Richtung gebildet, also auch die steigende, daher deren wahre Natur damals nicht erkannt wurde: den Griechen galt sie – die lydische Tonart – für weichlich […]. Umgekehrt herrscht in der europäischen Musik die steigende Richtung als alleiniges Bildungsgesetz, das auch der fallenden Skala, gegen deren eigentliche Natur, aufgezwungen wird.[17]

Zu verstehen sind Kauders Ansichten über eine naturgegebene, göttliche Ordnung der Musik auch vor dem Hintergrund seiner Haltung zu Fragen der Tonalität. In seiner 1960 veröffentlichten Kontrapunktlehre positioniert er sich gegen die Zwölftonmusik Schönbergs. Kauders Kontrapunktlehre setzt eine naturgegebene Tonalität (wenn auch mit »new principles«) voraus.

It is true that, owing to a long and consistent development, traditional tonality has lost its moving and shaping force, thus having become indifferent. It has been replaced by the artificial constructions of the ›twelve-tone system,‹ today widely regarded as the last word of music history. Yet it has to be said, with due reverence for Arnold Schoenberg’s great personality, that it can not be more than a mere expedient in a period of crisis and transition, and that even the most ingenious artifice sooner or later will be superseded by an art grown out of the moving and shaping forces of music itself. As these forces are inherent in the very substance of music, they will be rejuvenated, whenever time makes it necessary, out of the primordial source of music: the order of the universes and the accordance of human nature with this order.[18]

Die Idee der Ordnung des Universums äußert sich in Kauders Ansichten über die Grundformen der Skalenbildung. Als Vertreter des harmonischen Dualismus steht er in der von Hermann von Helmholtz geprägten Tradition. Auch Arthur von Oettingen (1836–1920), ebenfalls Vertreter einer dualistischen Lehrmeinung, wird von Kauder rezipiert, indem er sich in Bezug auf die Begrifflichkeiten explizit auf Oettingens Bezeichnungsweise bezieht. Soweit »Benennungen der Skalen unmittelbar aus ihrer Natur« bereits vorhanden seien, sollen sie übernommen werden. In Anlehnung an Oettingens Harmoniesystem in dualer Entwicklung (1866) sollen »entgegengesetzt gerichtete Dreiklänge« als Ober- und Unterklang bezeichnet werden – »anstatt der auf der falschen Anschauung von gleichgerichteter großer und kleiner Terz beruhenden Namen Dur und Moll.«[19] Bei Kauder führt der dualistische Ansatz zu einer radikalen Vermeidung der Begriffe »Dur« und »Moll«, die er in seiner Melodie- und Harmonielehre stets durch die Bezeichnung »Ober- und Unterklang« ersetzt.

Während Kauder diese dualistische Meinung und das Konzept einer Ober- und Untertonreihe in seiner Melodie- und Harmonielehre voraussetzt, führt er in seiner fast 30 Jahre danach veröffentlichten Kontrapunktlehre eingangs den Ursprung seiner Ansicht an: das universelle Gesetz der Polarität.

The two opposite series of partial tones and the two scales derived from them are the sounding realization of the universal law of polarity. Polarity, the primordial moving force of the universe and the origin of life on earth, also generated the basic elements of music.[20]

Als weitere Autorität ist im Hintergrund von Kauders Melodie- und Harmonielehre Hugo Riemann anzuführen. Nach einer kurzen Erwähnung im Vorwort, kommt Kauder im Kapitel »Harmonie und Polyphonie« konkret auf Riemann zu sprechen. Die »selbständige Weiterentwicklung der Akkordlehre bis zu einem umfassenden Perspektivismus« hätte dieser bereits geleistet.[21]

[…] freilich bleibt er [Riemann] in dem Grundirrtum befangen, die gesamte Musiktheorie und Kompositionstechnik auf die Lehre vom Dreiklang gründen zu wollen. Diese reicht aber nicht aus um allgemeingültige Bindungen zu schaffen und daher muss die Ausübung ihr oft widersprechen: eine Lehre, die den Akkord als Einheit nimmt, hat keine Geltung für eine Musik, die nicht bloße Folge von Akkorden ist, vielmehr gleichzeitiges Erklingen von Melodien: Polyphonie.[22]

Insbesondere bei der Verbreitung des dualistischen Prinzips decken sich die Ausgangslagen Riemanns und Kauders, wobei hinzugefügt werden muss, dass Riemanns Position zum Dualismus sich im Laufe der Jahre auch aufgrund der Einwände seitens einiger Akustiker stark veränderte und er seine Meinung hierzu mehrfach revidierte.[23] Ebenso wie bei Kauder verdankte sich auch bei Riemann die Hinwendung zum Dualismus der Begeisterung für Oettingens Schriften.[24] Michael Polth zählt Kauder zu einer Richtung der »harmonikalen Melodielehren«, da er die »Herleitung von Tonrelationen aus Verhältnissen der […] Oberton- und Untertonreihe von der Bildung der Akkorde auf die Ordnung der Diatonik« übertragen hat.[25]

Kurz nach dem Erscheinen von Kauders Publikation veröffentlichte auch Paul Hindemith seine Unterweisung im Tonsatz. Ein Vergleich der beiden Werke lässt die besonderen Eigenschaften von Kauders Skalentheorie umso deutlicher hervortreten. Hindemith schreibt über seine beiden Hauptprinzipien der Melodiebildung bekanntermaßen: »Welche Dienste leisten der Melodiestufengang und der Sekundgang dem Tonsetzer? Sie sind unentbehrlich bei der Analyse vorhandener Melodien.«[26] Und an anderer Stelle heißt es: »Die nachstehenden Notenbeispiele und die Zergliederung ihres Mechanismus sollen zeigen, daß mit der in diesem Buche niedergelegten Methode die Musik aller Stilarten und aus allen Zeiten analytisch zu erfassen ist.«[27]

Kauder hingegen versucht zwar, sich mit seiner Skalentheorie an »allezeit gültigen geistigen Gesetzen« zu orientieren, beabsichtigt aber nicht, ein Analyse- oder Kompositionswerkzeug für jegliche musikalische Stilistik zu entwerfen, sondern spezielle Prinzipien der Formung von Melodien vorzustellen. Das Hauptziel seiner Melodiebildung ist die Ausgewogenheit.[28] Der größte Unterschied zwischen den Melodielehren Hindemiths und Kauders liegt also in ihrem jeweiligen Anspruch.

Wie sich ihre unterschiedlichen musikalischen Idealvorstellungen auf die jeweilige Lehre auswirkten, soll an einem Beispiel gezeigt werden. So führt Hindemith in Regel 11 aus: »Mehr als zwei Sekundschritte in gleicher Richtung hintereinander sind nicht gut, weil sie als größerer Ausschnitt einer Tonleiter nur ganz geringe melodische Spannung haben […].«[29] Kauder hingegen sieht die Stufenfolge der Töne als oberstes Prinzip an und eine Gestalt mit einer langen schrittweise aufsteigenden Bewegung, gefolgt von einer langen absteigenden Bewegung, als ausgewogene Melodiebildung.[30] Hindemith leitet melodische Einheiten aus den Harmonien ab und spricht dementsprechend von der »harmonischen Anlage einer Melodie«,[31] ähnlich wie auch Schönberg die Harmonie als vertikale Melodie begreift und umgekehrt die Melodie als horizontale Harmonie.[32] Für Hindemiths Idee des melodischen Stufengangs findet sich bei Kauder keine Entsprechung. Insgesamt scheint der Ansatz, Melodien aus Harmonien heraus zu entwickeln und die immanenten harmonischen Aspekte von Melodien mitzudenken, für Kauder weniger Bedeutung gehabt zu haben. Kauders Musik zeichnet sich dadurch aus, dass ein Werk stets streng auf einer oder sehr wenigen Skalen beruht. Einheit entsteht durch eine ausgewogene Auf- und Abwärtsbewegung der melodischen Gestaltung und durch die Begrenzung auf wenige Skalen als melodisches Material. Mehr hierzu im Kapitel 3 dieses Beitrags.

Die chromatische Skala, die sowohl für Hindemith[33] als auch für Schönberg[34] zentral ist, spielt für Kauders Musik eine nur untergeordnete Rolle und wird von ihm auch in seiner Skalensammlung so gut wie gar nicht behandelt. Einzig wird erwähnt, dass die »chromatische Skala« (von Kauder in Anführungszeichen gesetzt!) keine »Skala im eigentlichen Sinne« sei, sondern das Material der zwölf Halbtonschritte innerhalb einer Oktav. Es bleibe ein »unverbrüchlicher Rangunterschied bestehen zwischen den sieben Stammtönen der diatonischen Skala und den durch halbtonweise Erhöhung oder Erniedrigung von ihnen abgeleiteten Zwischentönen.«[35]

Neben den genannten musiktheoretischen Einflüssen bzw. inhaltlichen Bezugspersonen Pannwitz, Lustgarten, Oettingen und Riemann sowie den weitgehend konträren Positionen Hindemiths und Schönbergs sollen zuletzt auch jene Komponisten mit in eine erste Kontextualisierung einbezogen werden, auf deren Werke und musikalische Ansichten sich Kauder bezieht. Neben eigenen Musikstücken (insbesondere aus seinem Geigenbüchlein) integriert er Beispiele von Johann Sebastian Bach und Ludwig van Beethoven sowie ein Zitat aus Richard Wagners Schrift Oper und Drama (1851).

2.2. Aufbau und Zielsetzung

Kauders Melodie- und Harmonielehre gliedert sich in drei Kapitel »Intervalle und Skala«, »Akkord und Kadenz« sowie »Harmonie und Polyphonie«. Jedes dieser drei Kapitel ist systematisch aufgebaut, indem es vom Einfachen zum Komplizierten und gegliedert in nummerierte Themenabschnitte voranschreitet. Für die gesamte Melodie- und Harmonielehre bleibt die Skala – insbesondere die geschlossene Skala[36] – das zentrale Prinzip.

Als Hauptziel seiner Lehre führt Kauder nicht die »Erneuerung alter Lehren« an, sondern die »Aufweisung unbedingt und allezeit gültiger geistiger Gesetze«. Damit würde, »vielleicht zum erstenmal, eine Skalenlehre gegeben« werden, »der sich die Lehre von Akkord und Kadenz, von Harmonie und Polyphonie ohne Zwang und Widerspruch zuordnen« ließe.[37] Die Harmonie sei als solche nur transzendent »in der Idee vorhanden«. Verwirklicht werde sie »durch den Kontrapunkt in einem Gefüge von Melodien«. Im Kapitel »Harmonie und Polyphonie« nennt Kauder die Skala »das Maß und die Mitte der Harmonie«.[38]

Die folgende Aufstellung zeigt die zentralen Inhalte seiner Skalentheorie, dargelegt im Entwurf einer neuen Melodie- und Harmonielehre:

I. Tetrachorde (steigendes Tetrachord, fallendes Tetrachord, doppelsinniges Tetrachord)

Die Basis von Kauders Melodie- und Harmonielehre bilden drei Formen von Tetrachorden. Aus diesen entwickelt er später Skalen, Melodien und Akkorde.

Basierend auf dem dualistischen Denken einer aufsteigenden und einer absteigenden Richtung an Tonreihen – entstanden aus der Idee einer Oberton- und einer Untertonreihe – entwickelt Kauder in einem ersten Schritt die spiegelkongruenten Tonreihen (Abb. 1) als Abbildung der harmonischen Teilung der Oktave.

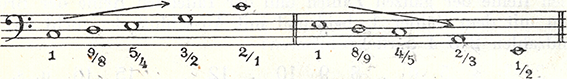
Abbildung 1: Hugo Kauder (1932), 10; spiegelkongruente Tonreihen

Durch Hinzufügung eines weiteren Tons (Abb. 2), den Kauder durch die Teilung der Oktav in Gegenrichtung (»die aufsteigende Oktave nach unten, die absteigende nach oben«) in Quint- und Quartintervalle findet, erreicht er in einem zweiten Schritt eine lückenlose Stufenfolge innerhalb eines Quintrahmens.

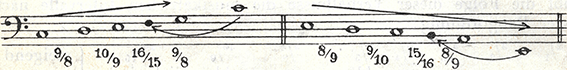
Abbildung 2: Hugo Kauder (1932), 10; lückenlose Stufenfolge Prim bis Quint

In einem dritten Schritt analysiert Kauder die Intervalle der in diesen Reihen enthaltenen Tetrachorde (vgl. Abb. 2). Da der Ton d aufgrund der Fundierung der Lehre in der reinen Stimmung in Kauders beiden Grundreihen nicht exakt der gleiche ist, unterscheidet er zwischen dem großen Ganzton (9/8 bzw. 8/9), dem kleinen Ganzton (10/9 bzw. 9/10) und dem diatonischen Halbton (16/15 bzw. 15/16).

Diese drei Qualitäten werden in den folgenden Abbildungen farblich markiert. Der hohe grüne Balken steht für den ›großen‹, der kleine grüne Balken für den ›kleinen‹ Ganzton und das rote Dach für den Halbton.

Da der große Ganzton (9/8 bzw. 8/9) in beiden Reihen (aufsteigend und absteigend) je zweimal vorkommt, lässt er je einen dieser Töne im vierten Schritt weg und kommt so zu vier Formen von Tetrachorden (Abb. 3).

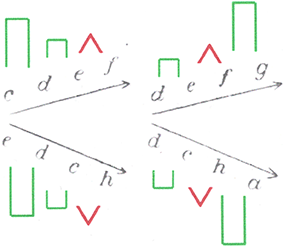
Abbildung 3: Hugo Kauder (1932), 10; Ausgangspunkt mit vier Formen von Tetrachorden; farblich markiert

Im fünften Schritt komprimiert Kauder diese vier Tetrachorde schließlich zu drei Grundformen. Das syntonische Komma würde in der musikalischen Praxis vernachlässigt werden, was Kauder zum Anlass nimmt, den ›großen‹ und den ›kleinen‹ Ganzton einander gleichzusetzen (Abb. 4). Dadurch erscheine »das zweite Tetrachord als symmetrisch« und falle »mit seinem Spiegelbild in eins zusammen«[39] (Abb. 5 und 6).

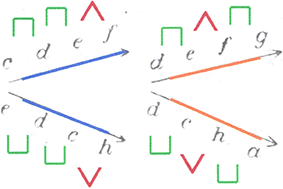
Abbildung 4: ›Großer‹ und ›kleiner‹ Ganzton gleichgesetzt; farblich markiert

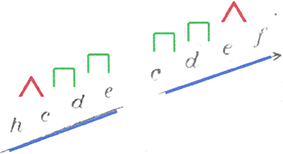
Abbildung 5: Erstes Tetrachord-Paar gespiegelt; farblich markiert

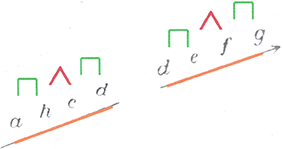
Abbildung 6: Zweites Tetrachord-Paar gespiegelt; wird bei Kauder zu einem Tetrachord; farblich markiert

Bei der Spiegelung des ersten Tetrachord-Paars (in Blau) erhält Kauder trotz der Angleichung des ›großen‹ und ›kleinen‹ Ganztons unterschiedliche Abfolgen, wenn die Tongruppen in Aufwärtsrichtung gelesen werden: Halbton–Ganzton–Ganzton und Ganzton–Ganzton–Halbton (Abb. 5). Bei der Spiegelung des zweiten Tetrachord-Paars (in Orange) ergibt sich aber – und das ist der entscheidende Punkt – zweimal die gleiche Abfolge: Ganzton–Halbton–Ganzton.

Diese Überlegung steht hinter Kauders Theorie von drei Grundtypen an Tetrachorden, auf denen seine Lehre fußt: 1.) das steigende Tetrachord, 2.) das fallende Tetrachord und 3.) das doppelsinnige Tetrachord.

II. Die Zusammenfügung zweier Tetrachorde zu Skalen

Aus den drei Grund-Tetrachorden bildet Kauder auf zweiter Ebene Skalen. Tetrachorde, die gleichgebaut und gleichgerichtet sind, werden kombiniert. Bei dieser Verbindung zweier Tetrachorde können entweder ein Ton gemeinsam sein (Abb. 7) oder zwei Tetrachorde mit einem Ganzton verbunden werden (Abb. 8). Die erste Form nennt Kauder »geschlossene«, die zweite »offene Skala« (die »geschlossene Skala« bezieht sich auf eine Tonika, wohingegen die »offene Skala« nur auf der Tonika beginnt und beliebig weit fortgesetzt werden kann). Die geschlossene Skala begreift er als »höhere und geistigere Form« und die »eigentliche Grundform der Skala« und die offene Skala als eine lediglich von der geschlossenen Skala abgeleitete Form.[40]

Abbildung 7: Hugo Kauder (1932), 11; Die drei Tetrachord-Grundtypen in geschlossenen Skalen

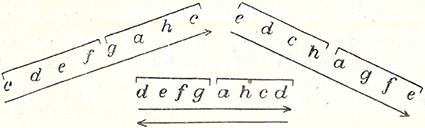
Abbildung 8: Hugo Kauder (1932), 12; Die drei Tetrachord-Grundtypen in offener Skala

Im letzten Schritt stellt Kauder die geschlossene Skala in »auseinandergelegter Form« dar, sodass die Tetrachorde mehrmals durchlaufen werden, um schließlich wieder in ihren jeweiligen Grundton zu münden. Durch diese letzte Umwandlung gelangt Kauder zu einer geschlossenen Skala, einem »Kreislauf um den Zentralton«, und zu der von ihm so bezeichneten »Urform der Melodie«.[41]

Abbildung 9: Hugo Kauder (1932), 12; Die »Urform der Melodie«

Die geschlossene Skala ist der Kern von Kauders Melodie- und Harmonielehre. Von diesem Punkt aus erweitert Kauder das von ihm vorgestellte System in die folgenden Richtungen:

III. Die Dominanten (Oberdominante, Unterdominante, Gegendominante, Unter-Gegendominante)

Eine erste Erweiterung erfolgt in der Darstellung der Dominanten als denjenigen Punkten, die am weitesten vom Grundton entfernt liegen (Wendepunkte der Skala). Die Dominanten seien durch die »äußerste Entfernung vom Zentralton« und daher die stärkste Spannung und Schlusswirkung charakterisiert.[42] Kauder unterscheidet zwischen Ober-, Unter, Gegen- und Unter-Gegendominanten. Mit »Oberdominante« bezeichnet er die Unterquart des Zentraltons der Oberskala (in Abb. 9 wäre hiermit der Ton g der Oberskala gemeint). Den Begriff »Unterdominante« verwendet er für die Oberquart des Zentraltons der Unterskala (das würde dem Ton a der Unterskala entsprechen). Die jeweils entgegengesetzte Richtung der Quarten nennt Kauder »Gegendominante« bei der Oberskala (in diesem Beispiel der Ton f der Oberskala) und »Unter-Gegendominante« in Bezug auf die Unterskala (der Ton h der Unterskala). Im Fall der doppelsinnigen Skala hätten die Dominanten jeweils doppelte Bedeutungen. Die Oberdominante der doppelsinnigen Skala wäre zugleich Unter-Gegendominante (der Ton a der doppelsinnigen Skala sowohl steigend als auch fallend) und die Gegendominante zugleich Unterdominante (der entsprechende Ton g). Die stärkste Spannung und Schlusswirkung hätten diejenigen Dominanten, bei denen in der Grundrichtung der Skala das letzte Intervall ein Halbton wäre. In der Oberskala habe die Oberdominante die stärkste Spannung, in der Unterskala die Unterdominante und in der doppelsinnigen Skala wären alle Spannungen der Dominanten gleichgewichtet, da keine mit einem Halbton zum Zentralton führen könne.[43]

IV. Die sechs abgeleiteten Skalen (drei Dominantskalen, drei Gegendominantskalen)

Eine zweite Erweiterung liegt in der Hinzufügung der Oktav, also eines achten Reihentones zu sechs abgeleiteten Skalen[44] (Abb. 10). Die Punkte in der Abbildung zeigen jeweils an, wo die Skalen erweitert wurden.

Abbildung 10: Hugo Kauder (1932), 14 f.; Die sechs abgeleiteten Skalen

V. Die chromatische Alteration (= »Jede Skala kann auf jeden beliebigen Ton transponiert werden.«)[45]

VI. Die halbtonlose fünfstufige Skala

Die siebenstufige Skala kann schließlich durch Weglassen der beiden »Halbtonschritte bildenden dritten« Quarten in eine fünfstufige Skala umgewandelt werden. Diese bezeichnet Kauder als »die harmonischeste [sic] aller Skalen«.[46]

Abbildung 11: Hugo Kauder (1932), 16 f.; links: Ineinander verkettete Quartintervalle in der siebenstufigen Skala; rechts: Die halbtonlose fünfstufige Skala

VII. Doppelgeschlechtige Skala (= elftönige Skala)

Abermals erweitert Kauder die geschlossene Skala durch die Verbindung der Ober- und Unterskala zur »doppelgeschlechtigen Skala« (= »ein getreues Abbild des kosmischen Kreislaufes: die kosmische Skala schlechthin«),[47] wobei die Töne der Oberskala nur in aufsteigender und die der Unterskala nur in absteigender Richtung erklingen sollen.[48]

Abbildung 12: Hugo Kauder (1932), 18; Doppelgeschlechtige Skala

VIII. Die gemischte Skala

Als komplizierte Erweiterung führt Kauder die gemischte Dominantskala an, die umgewandelt in der musikalischen Praxis der melodischen Mollskala entspricht.

Bemerkenswert ist jedoch ihre nicht umgewandelte Form (»steigende gemischte Skala«), die aus der Kombination von zwei einander entgegengerichteten Tetrachorden gebildet wird (Abb. 13). Diese Skala käme in der »neueren Musik« häufig vor, insbesondere seit Johannes Brahms (Abb. 14; vgl. mit Abb. 13, rechte Skala).

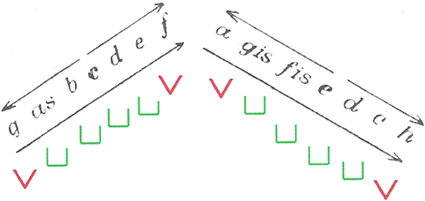
Abbildung 13: Hugo Kauder (1932), 18; Die gemischte Skala

Abbildung 14: Hugo Kauder (1932), 20; Beispiel einer steigenden gemischten Skala; Johannes Brahms, Sinfonie Nr. 4 op. 98, Beginn des »Andante moderato«

IX. Die Ganztonskala

Die eben vorgestellte gemischte Skala kann durch Erweiterung ihrer beiden Außentöne zu einer Ganztonskala ausgebaut werden (Erhöhung des obersten Tons und Erniedrigung des tiefsten Tons um jeweils einen Halbton). Daraus ergibt sich als einzige Form einer Ganztonskala die Tonfolge b-c-d-e-fis-gis-ais. Die Ganztonskala lasse sich »nur in geschlossener Form darstellen«, da die Erweiterung zur Oktave nicht wie bei den anderen offenen Skalen funktioniere beziehungsweise nur mit einer »enharmonischen Modulation« ihres obersten Tons darstellbar wäre, was dem Prinzip der Skala nicht entspreche.[49]

X. Die Grundgesetze der Melodiebildung

In einem letzten Schritt der Skalenlehre seines Entwurfs einer neuen Melodie- und Harmonielehre widmet sich Kauder den sogenannten Grundgesetzen der Melodiebildung. Er erinnert dabei an das »Urbild aller Melodie«, das aus der (aufgelösten) geschlossenen Skala bestehe. Grundgesetze der Melodiebildung seien demnach 1.) die Stufenfolge der Töne und 2.) das Gleichgewicht von Steigen und Fallen.[50]

Als wichtige Melodietypen führt Kauder die folgenden an:

a.) Wechsel von sprung- und stufenweiser Bewegung

Das Prinzip dieser Melodiebildung besteht darin, dass die Fortschreitungen prinzipiell stufenweise erfolgen. Wenn ein Melodiesprung stattfindet, wird er entweder davor oder danach in stufenweiser Fortschreitung aufgefüllt und somit ausgeglichen.

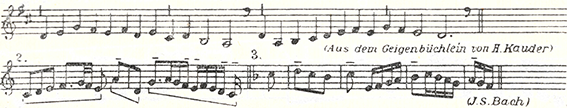
Abbildung 15: Hugo Kauder (1932), 21; Beispiele der sprung- und stufenweisen Abwechslung

b.) Wechselnde Auf- und Abwärtsbewegung

Diese Form der Melodiebildung ist dadurch gekennzeichnet, dass zwar Melodiesprünge vorkommen, diese aber durch wechselnde Auf- und Abwärtsbewegungen ausgeglichen werden müssen bzw. in übergeordnete Sekundbewegungen eingebunden werden sollen.

Abbildung 16: Hugo Kauder (1932), 21; Beispiele des Ausgleichs bei Melodiesprüngen, gezeigt am Wohltemperierten Klavier J. S. Bachs

c.) Bewegung in Sequenzen

Eine weitere Art der ausgeglichenen Melodieführung sieht Kauder in der stufenweise sequenzierten Abfolge von kurzen Melodieabschnitten.

Abbildung 17: Hugo Kauder (1932), 21; Sequenzierte Melodiebildungen, gezeigt an einem Werk J. S. Bachs

d.) Abwechslung von aufwärts und abwärts verlaufenden Abschnitten

Eine ausgewogene Melodiebildung liegt nach Kauder vor, wenn sich an einen ersten musikalischen Abschnitt, der in eine bestimmte Bewegungsrichtung läuft, ein weiterer Melodieabschnitt in entgegengesetzter Richtung anschließt. Eine Stufenfolge der Töne und der Ausgleich von Steigen und Fallen sind auch hier gegeben.

Abbildung 18: Hugo Kauder (1932), 22; Beispiel von aufwärts- und abwärtslaufenden Abschnitten

Konkrete Hinweise für die Anwendung seiner Lehre gibt Kauder am Ende des dritten kurzen Kapitels »Harmonie und Polyphonie«. Dort empfiehlt er, dass die Melodien auf der Grundlage strenger Skalen gebildet werden sollen. Des Weiteren sollen die Zusammenklänge an den Gliederungspunkten der Hauptmelodien beachtet werden und soll die Akkordlehre insgesamt als Teil der Kontrapunktlehre behandelt werden. Den Abschluss bildet ein Statement zur zugrundeliegenden musikalischen Substanz jeglicher Musik.

[…] das eigentlich Entscheidende ist zuletzt nur die zugrundegelegte musikalische Substanz. Ist diese selbst schon nach unverbrüchlichen geistigen Gesetzen geformt, so erweist sie sich für die Ausübung der Kunst als der ›Stein der Weisen‹, der, mit dem rechten Wissen und Können angewendet, alles in Gold zu verwandeln vermag.[51]

***

3. Eine Melodieanalyse von Kauders Kleiner Suite für Bratsche allein

Kauder, Bratschist im Gottesmann-Quartett, komponierte 1924 eine Kleine Suite für Bratsche allein (publiziert 1926) – also wenige Jahre vor der Veröffentlichung seiner Skalentheorie. Nach Karin Wagner steuerte Kauder seinen Überlegungen auch »die adäquate Musik bei«.[52] Es stellt sich daher im Anschluss an die Beschäftigung mit Kauders Skalentheorie die Frage, ob bzw. auf welche Weise dieser seine musiktheoretischen Überlegungen auch kompositorisch verwirklichte oder transformierte.

Die Skalen in Kauders Kleiner Suite für Bratsche allein

In seiner Kleinen Suite für Bratsche allein können einige seiner theoretischen Positionen aus seiner Skalentheorie in Anwendung beobachtet werden. Die Suite gliedert sich in die Teile Präludium, Etude, Melodie und Tanz.

Präludium

Abbildung 19: Hugo Kauder (1926), 2; Beginn Präludium

Eine erste melodische Gestaltungsweise lässt sich im Präludium erkennen. Wenn die Tonwiederholungen (unmittelbar und mittelbar) weggelassen werden, lässt sich der Tonvorrat des Präludiums als folgende Skala darstellen:

Abbildung 20: Skala des Präludiums; vgl. Hugo Kauder (1926), 2

Die Melodien des Präludiums bestehen folglich aus einer anhemitonischen pentatonischen Skala, die sich über drei Oktaven erstreckt. Diese Form der Pentatonik ist selbstverständlich nicht ungewöhnlich. In Kauders Melodie- und Harmonielehre erscheint sie als Ableitung aus der siebenstufigen Skala in der Form a-h-d-e-g (Ganzton – kleine Terz – Ganzton – kleine Terz).

Interessant sind hierbei – neben dem Tonmaterial an sich – auch zwei weitere Aspekte: erstens die Konsequenz, mit der sich Kauder innerhalb eines Stücks (Präludium) nur einer bestimmten Skala bedient, und zweitens die melodische Gestaltung in großen aufwärts-, dann abwärtsgerichteten Bögen. Eine in sich kreisende Bewegung, die für Kauder das Ideal einer guten und ausgewogenen Melodie ist, wird durch Wellenbewegungen erreicht. Anfangs- und Endton des Stücks ist d.

Etude

Abbildung 21: Hugo Kauder (1926), 2; Beginn Etude

Dass der zweite Teil seiner Kleinen Suite von Tetrachorden geprägt ist, erschließt sich auf den ersten Blick. Nach jedem Ton der Tetrachorde wird jeweils die leere Saite a eingeschoben. Im Großen kann das Stück in drei Teile eingeteilt werden:

1. Teil = Takte 1–5 (T. 5: Schlusston a) und Takte 6–10 (T. 10: Schlusston a)

2. Teil = Erweiterung in die Höhe, Takte 11–21 (T. 21: Schlusston a)

3. Teil = Teilreprise, dann Erweiterung zum höchsten Ton, Takte 22–26 (T. 26 Schlusston a) und Takte 27–40 (T. 38–39 Schlusston a)

Am Ende jedes Teils sowie am Schluss der ganzen Etude pendelt sich das Stück auf dem Ton a ein.

Insgesamt verwendet Kauder in der Etude drei Formen von Tetrachorden (Abb. 22), die auch auf andere Tonstufen transponiert werden.

Abbildung 22: Tetrachorde der Etude; vgl. Hugo Kauder (1926), 2 f.

Durch eine Kombination der transponierten Tetrachorde zeigen sich offene Skalen, die quasi beliebig über einen größeren Ambitus weitergeführt werden können. Zu einer großen Melodie verbunden werden die Tetrachorde über sequenzartige Fortschreitungen (vgl. oben in Abschnitt X.c, Bewegung in Sequenzen; Abb. 17).

Abbildung 23: Melodiefolgen; vgl. Hugo Kauder (1926), 3

Neben den stufenweise abwärts gerichteten Tetrachorden verwendet Kauder wiederholt zwei weitere Melodiefolgen (Abb. 23). Beide Abfolgen beruhen auf der neutralen offenen Skala – insbesondere bei den gelb markierten Abfolgen ist diese Ableitung deutlich, aber auch die blau markierte Abfolge lässt sich mit einem ergänzten f in eine neutrale Skala einordnen. Zur Bewegungsrichtung ist zu bemerken, dass Kauder hier die Melodiesprünge durch das Wechseln der Bewegungsrichtung ausgleicht (vgl. oben in Abschnitt X.b, wechselnde Auf- und Abwärtsbewegung; Abb. 16).

Melodie

Den dritten Teil der Suite nennt Kauder Melodie, und auch dieser Abschnitt beruht wie das Präludium auf einer pentatonischen Skala.

Abbildung 24: Hugo Kauder (1926), 4; Beginn Melodie

Die Satzüberschrift »Melodie« könnte implizieren, dass Kauder hier einen Satz komponiert hat, der seiner Vorstellung einer guten Melodieführung in besonderer Weise entspricht. Auffallend ist, dass Kauder hier – wie auch im Präludium – auf Taktstriche verzichtet. Stattdessen gliedert er die Melodie durch Kommata bzw. Atemzeichen. Die instrumentale Linie erinnert dadurch an ein vokal vorgetragenes Lied. Abgesehen von der pentatonischen Skala – im Gegensatz zum Präludium mit anderem Ambitus und anderem Zentralton (beim Präludium d, bei der Melodie a), jedoch dem gleichen pentatonischen Material (Skala siehe Abb. 25) – ist in Bezug auf die Melodieanalyse auffällig, dass Kauder hier einige Phrasen wiederholen lässt und sich so ein melodisch-motivischer Kern zeigt (zu den melodischen Beziehungen vgl. Abb. 26). Außerdem kann in diesem Satz die Anwendung von Kauders zweitem Grundgesetz der Melodiebildung – dem Gleichgewicht von Steigen und Fallen – beobachtet werden. Sowohl die Gestaltung der größeren Melodieteile zeichnet sich durch eine Wellenbewegung von Steigen und Fallen aus als auch die innere Struktur vieler Melodiefragmente (z. B. Abb. 27).

Abbildung 25: Skala der Melodie; vgl. Hugo Kauder (1926), 4

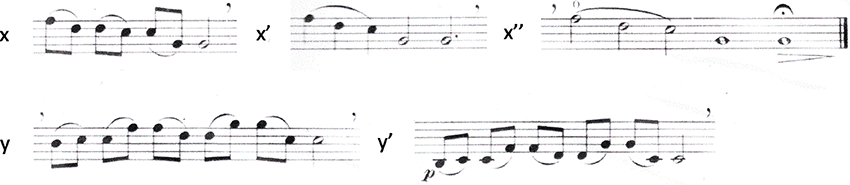
Abbildung 26: Hugo Kauder (1926), 4; Beziehungen (x, x’, x’’ gleicher melodischer Kern; y, y’ Verbindung durch simple Oktavversetzung der melodischen Figur)

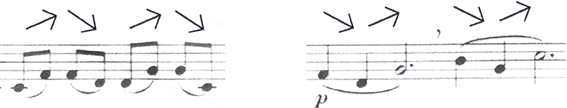
Abbildung 27: Hugo Kauder (1926), 4; Gleichgewicht von Steigen und Fallen der inneren Struktur

Interessant wäre es, den Blick auch auf die Anlage der Rhythmik zu lenken und auf den großen Bogen des Stücks: Wann gibt es bewegte Stellen, wann ruhige? Kann von einer großflächig angelegten Wellenform mit Belebung und Beruhigung (Steigen und Fallen) gesprochen werden? Diesen Fragen widmet sich Kauder in seinem Entwurf einer neuen Melodie- und Harmonielehre kaum. Möglicherweise wäre eine Annäherung an sie methodisch durch eine induktive Herangehensweise denkbar. Im Rahmen einer quantitativ größer angelegten Studie könnte über mehrere Melodieanalysen von Kauders Musik auf weitere (rhythmische und formale) Prinzipien seiner Melodiegestaltung geschlossen werden.

Tanz

Abbildung 28: Hugo Kauder (1926), 4; Beginn Tanz

Bemerkenswert am vierten Teil der Suite ist neben den zahlreichen stufenweise auf- und abwärts verlaufenden Skalen die offene Gestaltung im Hinblick auf einen möglichen Grundton. Wie auch in den Teilen Präludium, Etude und Melodie baut Kauder den Tanz auf drei Zentraltönen auf: d, a, e. Insbesondere in den Takten 19–23, 31–35 (= Ende 1. Teil) und 75–89 (hier wird bei »Wie anfangs« über das a zurückgeleitet) ist der Ton d sehr präsent.

Die offene Skala hebt die Beschränkung auf den Umfang einer Septime auf und verlegt den Grundton aus seiner zentralen Stellung an den Anfang der Reihe, die nunmehr durch den ganzen Töneraum beliebig fortgesetzt werden kann. Damit hört der Grundton auf, sichtbares Zentrum zu sein; er bleibt jedoch der geistige Mittelpunkt, auf den jeder Ton bezogen wird und von dem aus alle Töneverhältnisse abgemessen werden.[53]

Der tiefste vorkommende Ton ist das kleine d. Nach Kauders Skalenlehre baut auf diesem d folglich eine offene doppelsinnige Skala auf. Ausgehend von dieser Skala beschreibt Kauder in seiner Melodie- und Harmonielehre den Weg hin zu einer pentatonischen Skala (Abb. 29–31), und genau das ist im Tanz sichtbar. Neben der doppelsinnigen Skala treten mehrfach pentatonische Elemente in Erscheinung (vgl. etwa in Abb. 28 die grün markierte Passage). Diese beiden bei Kauder miteinander verwobenen Elemente der offenen Doppelsinnigkeit und der Pentatonik bestimmen das melodische Material der gesamten Suite. Im Gesamtbild wird noch einmal deutlich, dass Kauder sämtliche Tonhöhenbeziehungen aus einem einzigen Zentralton heraus entwickelt – hier dem kleinen d (zugleich dem allerersten Ton der Suite). Die Nähe seiner eigenen Skalentheorie zu seiner persönlichen Kompositionsweise scheint – zumindest durch diese Einzelstudie – bestätigt.

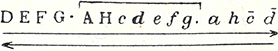
Abbildung 29: Hugo Kauder (1932), 14; Offene doppelsinnige Skala

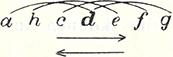
Abbildung 30: Hugo Kauder (1932), 16; Quartverhältnisse; Durch Auslassung der dritten Quart werden die Halbtöne eliminiert

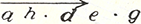
Abbildung 31: Hugo Kauder (1932), 17; Daraus entwickelte »halbtonlose fünfstufige Skala« (= Pentatonik)

4. Kritik und Ausblick

Selbstverständlich äußern wir heutzutage Kritik an Kauders dualistischem Konzept und der von ihm zur Grundlage seiner Melodie- und Harmonielehre erhobenen Auffassung einer derart hörbar gemachten Untertonreihe. Kauders Skalentheorie kann als Mittel zur Annäherung an seine Musik neue Einsichten in Kauders Kompositionsweise eröffnen. Schon anhand der Melodieanalyse seiner Kleinen Suite wird sein kompositorischer Zugang zu Skalen deutlich. Auch in anderen Werken wie seinen Streichquartetten oder auch dem von ihm in seiner Melodie- und Harmonielehre angeführten Geigenbüchlein spiegeln sich seine musiktheoretischen Überlegungen und musikästhetischen Ideale wider.

Kauders Entwurf einer neuen Melodie- und Harmonielehre wurde sowohl im deutschsprachigen Raum als auch später in den USA rezipiert. Eine Rezension von Hans Ferdinand Redlich aus dem Jahr 1932 zeigt erste Reaktionen auf das Buch.[54] Über seine Schüler wurde Kauders Melodie- und Harmonielehre und später auch sein Lehrbuch zum Kontrapunkt weiterverbreitet. Kauder unterrichtete Personen wie Josef Mertin, Julius Chajes, Eric Zeisl, Erwin Weiss und Hans Schimmerling.[55] Beispielsweise übernahm Chajes Kauders Skalentheorie und seine Kontrapunktik.[56]

Der theoretische Teil von Kauders später Kontrapunktlehre (Counterpoint. An Introduction to Polyphonic Composition, 1960) setzt bei der Skalentheorie an, die dadurch auch im englischsprachigen Raum noch weitere Verbreitung fand.

Kauder wurde als Komponist bisher nur in ersten Ansätzen aus dem ›Verstummen‹ herausgeholt und als Musiktheoretiker weitenteils noch gar nicht erforscht. Zahlreiche Beiträge in den Musikblättern des Anbruch wie auch weitere Aspekte seiner Melodie- und Harmonielehre sowie seiner Kontrapunktlehre warten auf ihre musiktheoretische Erforschung. Nicht nur können seine Schriften über bisher wenig beachtete Facetten der Geschichte der Musiktheorie Aufschluss geben, sondern auch konkret über die Beschaffenheit seiner Musik.