Vom Satzmodell zum Modell
Ulrich Kaiser
In dem folgenden Beitrag wird vom ›Satzmodell‹ (›Satztypen und -formeln‹ im Sinne von Carl Dahlhaus) ausgehend ein Modellbegriff entwickelt, der die Anforderungen empirischer Forschung im Bereich der musikalischen Analyse erfüllt. In einem ersten Schritt werden hierzu die Möglichkeiten und Grenzen des Begriffs ›Satzmodell‹ erörtert. In einem zweiten Schritt wird gezeigt, dass sich die Eigenschaft Formfunktion nicht über Satzmodelle, sondern nur über weitere Modelle (Metamodelle), beschreiben lässt, wie z.B. die in verschiedenen Diskursen (Schenkerian Analysis, Partimento) verwendete Tonleiterstruktur. Abschließend werden ausgewählte Modelle mithilfe der Unified Modelling Language (UML) skizziert und der Wert des Modelldesigns für eine wissenschaftliche Forschung im Sinne Niklas Luhmanns aufgezeigt.
Taking the idea of the ›Satzmodell‹ (compositional types and formulas as defined by Carl Dahlhaus) the following article develops a concept of musical models which meets the demands of empirical research in the field of musical analysis. In a first step, the possibilities and limitations of the concept of the ›Satzmodell‹ will be discussed. In a second step, it will be shown that the property of formal function cannot be described in terms of schema theory, but requires further models (metamodels), such as scale structure, as used in various discourses (Schenkerian Analysis, Partimento). Finally, selected models will be outlined using the Unified Modelling Language (UML) and the value of model design for scientific research in the sense of Niklas Luhmann will be demonstrated.
Das Denken in Intervallsätzen und Satzmodellen, wie es von Carl Dahlhaus insbesondere in seinen Untersuchungen über die Entstehung der harmonischen Tonalität[1] dargelegt worden ist, hat den musiktheoretischen Diskurs in Deutschland nachhaltig beeinflusst. Denn die Satztypen und -formeln des 15. und 16. Jahrhunderts wie Kadenz, Quintfallsequenz und Dur-Moll-Parallelismus inklusive ihrer Vorformungen haben sich in Forschung und Lehre[2] als wertvolle Instrumente für die musikalische Analyse erwiesen.
Die Grundformen der von Carl Dahlhaus beschriebenen Satzmodelle sind sehr abstrakt. Der Canon von Johann Pachelbel beispielsweise dürfte der ›locus classicus‹ des Parallelismus-Satzmodells[3] sein, doch selbst das Entdecken eines Parallelismus in diesem Werk erfordert die starke Reduktion einer komplexen Wirklichkeit, da unzählige Tonbeziehungen der Komposition auf wenige Tonverhältnisse des Satzmodells reduziert werden müssen:
Beispiel 1: Grundform des Satzmodells Parallelismus
Ist eine lebensweltliche Komplexität (Musik) auf ein Satzmodell reduziert worden, ermöglicht diese Reduktion den Aufbau einer gedanklichen Komplexität[4] durch musikalische Operationen wie Stimmtausch, Chromatisierung, Prolongation und Synkopierung. Das Satzmodell in Beispiel 2 beispielsweise klingt anders als die Grundform des Parallelismusmodells in Beispiel 1, lässt sich aber dennoch als Ableitung dieses Satzmodells verstehen:
Beispiel 2: Komplexes Satzmodell und Komplexitätsreduktion zur Satzmodell-Grundform
Nach Niklas Luhmann ist es Ziel wissenschaftlicher Theoriearbeit, »Gleichheiten an etwas, was zunächst als ungleich erscheint«[5] festzustellen, da solche Vergleiche den Bereich praktischer Substitutionsmöglichkeiten erweitern. Im Bereich der musikalischen Analyse ermöglicht die Abstraktheit von Satzmodell-Grundformen Feststellungen dieser Art. Im Folgenden werden auf der Grundlage des Parallelismus-Satzmodells der Beginn des Präludiums in C-Dur BWV 924 von Johann Sebastian Bach sowie die Überleitung der Exposition aus dem Kopfsatz der 3. Sinfonie Es-Dur op. 55 von Ludwig van Beethoven, Takt 37–45, verglichen:
Beispiel 3: Komplexe Ausprägungen der Grundform des Parallelismus-Satzmodells: J.S. Bach, Präludium C-Dur BWV 924, T. 1–6 (Ausprägung I), L.v. Beethoven, op. 55, i, T. 37–45 (Ausprägung II)
Der Vergleich phänomenal unterschiedlicher Gegenstände wird dabei von einem spezifischen Erkenntnisinteresse geleitet: Im Hinblick auf die Beispiele von Bach und Beethoven lässt sich beispielsweise zeigen, dass der terzweise fallende Parallelismus als jeweils zweite Taktgruppe vorkommt und an dieser formalen Position nicht-modulierend und modulierend eingesetzt werden kann. Im Präludium Bachs führt das Satzmodell von der III. Stufe (e-Moll) zur Subdominante (F-Dur), von wo aus über das Basstetrachord F–C wieder die Ausgangstonart erreicht wird. In der Sinfonie Beethovens verbindet der Parallelismus die Grundtonart Es-Dur mit einem halbschlüssig wirkenden F-Dur-Akkord (Halbschluss der Nebentonart bzw. 3. Absatz nach Heinrich Christoph Koch[6]). Diese Halbschlusswendung bzw. Folge ›übermäßiger Quintsextakkord → Dominante der Nebentonart‹ kann dabei sowohl als eine der Subdominante angehängte Halbschlusswendung als auch als Bestandteil des Satzmodells interpretiert werden:[7]
Beispiel 4: L.v. Beethoven, op. 55, i, T. 37–45; Halbschlusswendung als chromatisiertes Glied des Parallelismus-Satzmodells
In der Sinfonie Beethovens wurden die Akkorde Es-Dur, c-Moll, As-Dur und F-Dur verbunden, im Präludium Bachs die Akkorde e-Moll, C-Dur, a-Moll und F-Dur. Zusammenfassend lässt sich also sagen, dass ein Parallelismus den Zusammenhang von Akkorden auf einer Terzachse herstellt, wobei die Wirkung (z.B. nicht-modulierend oder modulierend) von weiteren Faktoren wie z.B. Chromatik, Metrik, Dynamik etc. abhängig ist.
Eine Analyse mithilfe von Satzmodellen hat jedoch nicht nur Vorzüge. Ihr Hauptproblem liegt darin, dass sie einen musikalischen Verlauf zerteilt, und zwar in Satzmodelle und Nicht-Satzmodelle. Einwände, die gegen Satzmodellanalysen immer wieder erhoben werden, erinnern zu Recht daran, dass ein Zerlegen von Musik keine musikalische Analyse sei, weil das synthetische Moment fehlen würde, also im Falle einer Satzmodell-Analyse das Bestimmen der Funktion von Satzmodellen für das Werkganze. Bezieht man den Begriff Satzmodell ausschließlich auf die Dimension, in der sich die Notenbeispiele in den Schriften von Carl Dahlhaus bewegen, ist dieser Vorwurf sicherlich naheliegend. Satzmodelle transportieren zwar mehr Informationen zur Stimmführung als Funktions- oder Stufensymbole, zur Veranschaulichung der Formfunktion von Satzmodellen für das Werkganze benötigt man jedoch weitere, übergeordnete Modelle. Im Folgenden werden an zwei Beispielen solche übergeordneten Modelle veranschaulicht:
1.) Claudio Monteverdis Madrigal Si ch‘io vorrei morire aus dem IV. Madrigalbuch (1603) ist in mehrfacher Hinsicht außergewöhnlich. In diesem Stück kann man einen Undezimenakkord entdecken, von dem ›dahlhausinformierte‹ Leserinnen und Leser selbstverständlich wissen, dass er als Klangereignis um 1600 als ein manieristischer Dissonanzgebrauch zu dechiffrieren ist. Darüber hinaus erklingen auffällig ausgedehnte 5-6-Konsekutiven und 7-6-Synkopenketten sowie Quintfall- und Parallelismussequenzen. Nicht zuletzt wird ein Ambitus für die Einzelstimmen von beinahe zwei Oktaven durchschritten. Versucht man einen Sinn in der Abfolge der Sequenzen zu erkennen, ist es am aufschlussreichsten, sich auf den Klangraum zu konzentrieren:
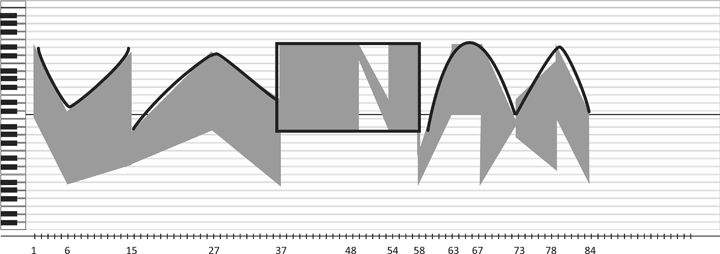
Beispiel 5: C. Monteverdi, Si ch‘io vorrei morire, Klangraumdiagramm
Von einem auffälligen Block abgesehen – etwa in der Mitte des Stücks (T. 37–58) –, in dem Monteverdi den Klangraum zwischen e2 und a bis auf eine kleine Unterbrechung relativ konstant nutzt, geht es in diesem Madrigal zu wie in einer Achterbahn. Das Klangraummodell ist in der Lage, die Abfolge von Satzmodellen zu erklären und gleichzeitig die Möglichkeiten zu limitieren, welches Satzmodell an welcher Stelle des musikalischen Verlaufs vorkommen kann. Im Sinne einer Steigerung gedanklicher Komplexität wäre es zudem möglich, die Art der Bewegungen zu unterscheiden, vergleichbar mit den Differenzierungen, die Wolfgang Krebs in Anlehnung an Ernst Kurth mit ›Fluktuationswelle‹, ›Expansionswelle‹ und ›Degressionswelle‹ für die energetische Beschreibung sinfonischer Musik des ausgehenden 19. Jahrhunderts vorgeschlagen hat.[8] Darüber hinaus wäre es interessant zu untersuchen, ob sich über Klangraummodelle auch Erkenntnisse bezüglich der Formfunktion von Satzmodellen in Musikwerken beispielsweise des 18. Jahrhunderts gewinnen lassen.
2.) Ein weiteres Modell, mit der sich die Formfunktion von Satzmodellen veranschaulichen lässt, ist die Tonleiter. Tonleiterstrukturen kommen in verschiedenen musiktheoretischen Diskursen vor, zum Beispiel als Oktavregel (›Regola dell’ottava‹) im Bereich der Partimento-Forschung oder als Oktavzug im Bereich der graphischen Analyse nach Heinrich Schenker.[9] Recht bekannt ist zum Beispiel Schenkers Analyse des Präludiums in C-Dur aus dem ersten Teil des Wohltemperierten Klaviers von Johann Sebastian Bach.[10] Heinrich Schenker stellt fest, dass in diesem Stück der C-Dur-Tonleiter im Bass »die Führung zugestanden werden [muss], trotzdem die Oberstimme den Urlinie-Ton hat […]«:
Beispiel 6: J.S. Bach, Präludium in C-Dur BWV 846, Analysediagramm von Heinrich Schenker[11] (oben) und Analysediagramm von Ulrich Kaiser (unten)
In dem oberen Diagramm ist das Strukturmodell Basstonleiter (c1–c) zu sehen, im unteren eine Harmonik- und Stimmführungsskizze, die der Analyse Schenkers nur in groben Zügen folgt. Für die nachstehenden Ausführungen werden darüber hinaus die beiden verminderten Septakkorde über cis und h als klangliche Varianten der Dominantakkorde A-Dur und G-Dur aufgefasst. Durch diese Veränderung wird die Mechanik der Quintfallsequenzen als 2-3-Synkope zwischen struktureller Oberstimme und Bass mit einer 6-5-Seitenbewegung unter der Agensstimme (also der strukturellen Oberstimme) ersichtlich, wobei sich über die gleiche kontrapunktische Bewegung auch der Einstieg in die Sequenz bzw. der Übergang von C-Dur nach a-Moll erklären lässt.
Beispiel 7: J.S. Bach, Präludium in C-Dur BWV 846, Analysediagramm zur Veranschaulichung der Formfunktion der Sequenzen
Anhand der Tonleiter lassen sich nun die Formfunktionen der Satzmodelle gut beschreiben: Die erste Sequenz führt von der Ausgangstonart in die Oberquinttonart, die zweite von der Oberquinttonart wieder zurück in die Ausgangstonart.
Für die folgenden Ausführungen soll es nicht von Bedeutung sein, dass die graphische Analyse an einem Präludium Bachs entwickelt worden ist. Das Diagramm ist vielmehr als generalisierte Konstruktion zum Verständnis des Verlaufs einer tonalen Komposition anzusehen. Der Wert dieser Konstruktion wird daran zu bemessen sein, ob sie in der Lage ist, Erkenntnisse über den Verlauf eines musikalischen Werkes zu veranschaulichen.
Beispiel 8: Generalisierter Verlauf einer tonalen Komposition
Wird das Diagramm in diesem Sinne aufgefasst, zeigt es zu Beginn eine Modulation in die Oberquinte, deren harmonischer Verlauf durch die Tetrachordstruktur im Bass (c-h-a-g) geprägt ist. Andere Harmonisierungen dieses Basstetrachords wären mit gleicher Wirkung (Modulation) denkbar, z.B. die Folge C-Dur, G-Dur, D-Dur und G-Dur. Abbildung 1 gibt eine Übersicht über Werke Mozarts, in denen sich der harmonische Verlauf der Überleitung in der Exposition über die genannte Tetrachordstruktur verstehen lässt:[12]
Abbildung 1: Liste strukturell vergleichbarer Überleitungen im Werk W.A. Mozarts
Die Oberquintmodulation symbolisiert zudem auf einer sehr abstrakten Ebene den Kern einer Sonatenexposition, wobei die fehlenden Abschnitte als Prolongationen interpretiert werden können: Eine Ausformulierung der I. Stufe vor der Modulation hätte demnach die Funktion eines Hauptsatzes, nach dem Erreichen der Nebentonart wäre ein Halbschluss zur Vorbereitung einer Seitensatzgestaltung denkbar, die anschließend durch Kadenzen in der Nebentonart beschlossen werden könnte.
Nach der Oberquintharmonie folgt die Stufenfolge VI#-II-V-I bzw. das Fonte-Satzmodell im Sinne Joseph Riepels. Dieses Satzmodell ist nicht nur typisch für Menuett-Mittelteile, sondern auch für Durchführungen in den frühen Werken Mozarts. An diesen Kompositionen lässt sich zudem beobachten, dass Mozart das harmonische Durchführungsziel (VI. Stufe in Durkompositionen) durch eine Verschiebung im Quintenturm bewerkstelligt (VI#-II-V-I wird zu III#-VI und VI-II-V-I).[13] Abbildung 2 benennt für die Durchführungsstruktur ›Fonte‹ einige Referenzwerke des jungen Komponisten:
Abbildung 2: Frühe Werke von W.A. Mozart, deren Durchführungen sich über die Struktur der Fonte-Sequenz beschreiben lassen.
Die Wiederkehr der Ausgangstonart symbolisiert im Analysediagramm von Beispiel 8 die Reprise.
Es wurde bereits erwähnt, dass die Quintfallsequenz durch die Harmoniefolge C-G-D-G substituiert werden kann, ohne die Wirkung ›Oberquintmodulation‹ zu gefährden. Quintfallsequenz und Pendelharmonik wären in diesem Fall funktional äquivalente Harmonisierungen des strukturellen Basstetrachords mit einer Oberstimme in Terzparallelen. Doch selbst dann, wenn das Analysediagramm zu einer Tonleiter in Terzen generalisiert wird[14] (Bsp. 9 mittig und unten), lassen sich noch funktionale Äquivalenzen aufzeigen. Zum Beispiel könnte die Oberstimme vom e2 bis zum h1 abwärts durch eine Aufwärtsbewegung von c1 bis g2 substituiert werden (Bsp. 9 mittig, mittleres System und unten):
Beispiel 9: Generalisierter Verlauf einer tonalen Komposition, funktional äquivalenter Tonhöhenverlauf zur fallenden Linie im Modulationsabschnitt bzw. der Exposition
Diese Reduktion ähnelt in auffälliger Weise einem bekannten Kinderlied, so dass pointiert formuliert werden könnte, dass sowohl die Tonleiterbewegung in Terzen als auch Alle meine Entchen (mit Chromatisierung der IV. Tonstufe aufwärts) den Verlauf einer Sonatenkomposition im Speziellen oder einer tonalen Komposition im Allgemeinen symbolisieren. Die in Beispiel 9 gezeigte Alle meine Entchen-Melodie in Es-Dur soll im Folgenden als ein Instrument musikalischer Analyse zur Beschreibung des Liedes An den Mond von Franz Schubert verwendet werden:
Beispiel 10: F. Schubert, An den Mond[15] und Analyseinstrument Alle meine Entchen zur Erklärung des formalen Verlaufs
Nach einem Vorspiel, das sich als Ausprägung eines Satzmodells verstehen lässt[16], folgt eine variierte Wiederholung des Abschnitts mit Gesang. Diese Taktgruppe dient der Ausformulierung der I. Stufe bzw. Grundtonart (im Sinne eines Hauptsatzes). Ihr folgt ein zweiter, modulierender Abschnitt (mit der Struktur einer Überleitung), deren Verlauf sich durch den Aufgang des Kinderliedes verstehen lässt. Die Harmonisierung Es-B-F-B entspricht dabei der im Zusammenhang mit dem Präludium Bachs und in den zahlreichen Werken Mozarts nachgewiesenen Pendelharmonik (C-G-D-G bzw. IV-I-V-I in der Nebentonart). Sechster und fünfter Ton des Kinderliedes charakterisieren ein Subdominant-Tonika-Pendel, wobei als eine funktional äquivalente Harmonisierung der Töne in dieser Formfunktion bereits das Fonte-Satzmodell erwähnt worden ist. Eine II-V-I-Harmonik (f-B-Es) bekräftigt an der Position der Tonstufen vier und drei des Kinderliedes (As-G) die Wiederkehr der Ausgangstonart, eine Kadenz (C-f-B-Es) beschließt die Gesangsstrophe, ein Klaviernachspiel die Komposition.
In Lehrerfortbildungen und Seminaren lasse ich die Entchen-Melodie gerne als Plot singen. Eine impulsive und ehrliche Reaktion kam dabei einmal von einer Studentin eines Seminars, die ihr Singen auf dem sechsten Ton abbrach und entsetzt vor sich hinmurmelte: »O Gott!« Doch worin liegt die Provokation in dem Kinder-Kunstlied-Experiment eigentlich genau?
Dass wir beim Analysieren die Aufmerksamkeit auf Details richten, ist so selbstverständlich, dass eine Erwähnung überflüssig erscheint. Wird nun aber, wie in dem Experiment, die gedankliche Konstruktion ›Kinderlied‹ durch Singen oder eine Soundfile-Manipulation zum Erklingen gebracht, fällt die Diskrepanz zwischen einer stark auf dieses Teilmoment gerichteten Aufmerksamkeit und einer auf das Ganze zielenden ästhetischen Wahrnehmung auf. Diese Diskrepanz kann als erhellendes Bonmot, ästhetisch aber auch als Provokation empfunden werden. Gedankliche Konstrukte wie das Kinderlied oder Tonleitern sind vergleichbar mit den Idealtypen Max Webers. Denn der Historiker und Soziologe hat bei seinem auf Begriffsbildung zielenden Terminus ›Idealtypus‹ großen Wert darauf gelegt, dass dieser nicht empirisch real sein dürfe. Ein Idealtypus »wird gewonnen durch einseitige Steigerung eines oder einiger Gesichtspunkte und durch Zusammenschluss einer Fülle […] von Einzelerscheinungen […] zu einem einheitlichen Gedankenbilde. In seiner begrifflichen Reinheit ist dieses Gedankenbild nirgends in der Wirklichkeit empirisch vorfindbar […]«.[17] Der Terminus Idealtypus ist im letzten Jahrhundert des Öfteren missverstanden worden, auch Carl Dahlhaus hat den Fachbegriff Idealtypus in seinen frühen Schriften nicht im Sinne Webers verwendet, worauf Philip Gosset in seinem Aufsatz »Carl Dahlhaus and the ›Ideal Type‹« hingewiesen hat.[18] Dahlhaus hatte in Analyse und Werturteil noch angemerkt: »der Idealtypus einer musikalischen Form – der Sonate oder der Fuge – der im späten 19. Jahrhundert allmählich zum Schema verblaßte und schließlich zum Etikett herunterkam, hatte um 1800 noch geschichtliche Substanz; er war musikalisch real.«[19] Der Unterschied der Ansichten ist gravierend, denn nimmt man an, dass ein Idealtypus irgendwann Realität besessen haben könnte, impliziert diese Anschauung die Unterscheidung eines zeitlichen Davor und Danach und leistet der Konstruktion einer Entwicklungs- und Zerfallsgeschichte Vorschub. Geht man mit Weber hingegen davon aus, dass zum Wesen eines Idealtypus sein utopischer Charakter gehört, kann es gar keine Zerfallsgeschichte geben, sondern lediglich unangemessene Idealtypen, die natürlich im Rahmen empirischer Forschung aktualisiert werden könnten.
Gute Idealtypen wie die Kinderlied- oder Tonleiterstruktur ermöglichen es, einen musikalischen Gegenstand wie das Lied Schuberts aus einer ganz spezifischen Perspektive zu vermessen.[20] Und diese Perspektive kann dann aufgrund eines Forschungsprogramms erwünscht, aufgrund eines anderen missbilligt werden.
Die musikwissenschaftliche Gepflogenheit, musiktheoretische Fragestellungen über Geschichtsdarstellungen zur Musiktheorie zu beantworten, hat dazu geführt, dass die Suche nach Idealtypen bzw. systematisches musiktheoretisches Denken in Deutschland heute kaum noch in der Musikwissenschaft, dafür aber in der institutionellen Musiktheorie stattfindet. Die Stigmatisierung systematischer musiktheoretischer Überlegungen als Dogmatismus erfüllt dabei vielenorts die Funktion einer Ab- und Ausgrenzung der Musiktheorie aus dem Verbund der Wissenschaftsfächer. Im Sinne von Carl Dahlhaus ist diese Entwicklung sicherlich nicht. Er hat nicht nur musiktheoretisches Arbeiten als wissenschaftsfähig erachtet[21], sondern auch daran erinnert, dass die systematische Musikwissenschaft (heute wäre hier zu ergänzen: die systematische Musiktheorie als eigenständiges Fach) »sich von der Historie weniger durch den Gegenstand [unterscheidet], den sie behandelt, als durch die Perspektive, in der sie ihn betrachtet. […] Eine vernünftige Wissenschaftspraxis kann nicht darin bestehen, daß man […] der Chimäre einer lückenlosen ›Synthese‹ von Historie und Systematik nachjagt. Es genügt vielmehr, die prinzipielle wechselseitige Ergänzungsbedürftigkeit der Disziplinen […] nicht zu vergessen […] und sich von Fall zu Fall von der anderen Seite das Ausmaß an gedanklicher und terminologischer Differenzierung anzueignen oder auszuleihen […].«[22] In der Praxis funktioniert das Ausleihen heute leider nicht immer gut, obwohl systematische musiktheoretische Erkenntnisse durchaus gesellschaftsrelevant sein können, weil sie praxisnahe pädagogische Perspektiven für den Musikunterricht eröffnen und dabei helfen können, einer zugrunde gerichteten Musiktheorie an den Schulen wieder auf die Beine zu helfen.
Im Folgenden möchte ich versuchen, meinen derzeitigen wissenschaftstheoretischen Standpunkt mithilfe von einigen Stichpunkten zu skizzieren:
Der Begriff des Idealtypus und seine komplizierte Rezeption durch Soziologen und Historiker legen Missverständnisse nahe. Ich versuche deshalb, diesen Terminus zu vermeiden. Weitere Einwendungen gegen den Begriff Idealtypus könnten sich darauf berufen, dass Max Weber ihn für Begriffsbildungen und nicht für Notendiagramme entwickelt und dass er für seine eigenen empirischen Forschungen keine auf Idealtypen basierende Methodik ausgearbeitet hat.[23]
Auch der Begriff des Satzmodells leistet Missverständnissen Vorschub. Für mich ist ein Satzmodell eine abstrakte gedankliche Konstruktion, die selbst dann nicht musikalisch real wäre, wenn alle Töne des Satzmodells mit den notierten Tönen eines Musikstücks übereinstimmen würden, da das Notat selbst nur eine Abstraktion im Hinblick auf die durch sie repräsentierte Musik ist. Für jemanden, der über Satzmodelle improvisiert oder sie am Klavier übt, dürfte eine solche abstrakte Vorstellung nicht unmittelbar verständlich sein.
An Stelle von Idealtypus und Satzmodell verwende ich den Begriff des Modells. Musiktheoretische Modelle sind komplexitätsreduzierte bzw. generalisierte Baupläne eines natürlichen oder fiktiven Originals, also einer erklingenden Musik oder eines anderen Modells. Ein Modell beschreibt seinen Gegenstand nicht auf der Grundlage einer 1:1-Beziehung, sondern ermöglicht durch 1:n-Beziehungen die Vergleichbarkeit von Dingen, die phänomenal als sehr ungleich erscheinen können.
Die Eigenschaften eines Modells sind darüber hinaus als Variablen zu denken, so dass kein Eigenschaftswert an sich als konstitutiv für das Modell genommen werden kann.
Die üblicherweise über ein Metamodell wie die Tonleiter veranschaulichte Formfunktion kann in das Modell hineinkopiert werden und wie die Harmonik eine Eigenschaft des Modells sein.
Das Konstant-Halten eines bestimmten Eigenschaftswertes erlaubt es, für andere Eigenschaften funktionale Äquivalente aufzuzeigen. Das Konstant-Halten der Formfunktion (beispielsweise: führt als zweite Taktgruppe in die Oberquinte) ermöglicht das Aufzeigen funktional äquivalenter Eigenschaftswerte z.B. für die Harmonik, also Substitutionsmöglichkeiten für eine bestimmte Harmoniefolge. In dem vorhin beschriebenen Oberquint-Modulationsmodell waren z.B. die Harmoniefolgen C-G-D-G und das Satzmodell Quintfallsequenz funktional äquivalent, wurden als unterschiedliche Eigenschaftswerte ein und desselben Modells (Tetrachord c-h-a-g) aufgefasst.
Modelle werden zur Beantwortung von Forschungsfragen gebildet, daher kann die Anzahl möglicher Modelle nicht begrenzt sein. Oder in der Sprache der Systemtheorie nach Niklas Luhmann: Modellbildungen sind kontingent. Und ebenso wenig, wie sich Welterfahrung einschränken lässt, kann die Kontingenz einer Modellbildung eingeschränkt werden. Die Forderung einer generellen Limitierung von Modellen für das wissenschaftliche Arbeiten lehne ich vor diesem Hintergrund als willkürlich und dogmatisch ab.
Die für Forschungsfragen notwendige Limitierung leistet das Zusammenspiel von Theorie[24] und Methode[25] in Anlehnung an Niklas Luhmann. Für die musiktheoretische Forschung verstehe ich unter Theorie zusammenhängende und auf einen musikalischen Gegenstand zielende Aussagesätze, unter Methode deren empirische Überprüfung unter Verwendung geeigneter Modelle. Dadurch, dass ein Scheitern einer methodischen Überprüfung eine Modifikation theoretischer Sätze nach sich zieht, eine veränderte Theorie dagegen die Modifikation der ihr zugehörigen Methode bewirkt, entsteht ein Kreislauf, der die für Forschungsvorhaben notwendige Begrenzung bereitstellt, ohne dogmatische Grenzen zu ziehen. Oder, um es mit einem Paradox Niklas Luhmanns auszudrücken: »Limitationen ohne Limitation also!«[26]
Das abschließende Beispiel dient der Veranschaulichung des Denkens in Modellen in der analytischen Praxis. Zur Veranschaulichung des Modelldesigns wird die Unified Modeling Language (UML 2.0) verwendet:
Beispiel 11: UML-Diagramm zum Design eines Modells, das dem herkömmlichen Verständnis eines Satzmodells entspricht
Beispiel 11 veranschaulicht, dass das Modell mit der VI#-II-V-I-Harmoniefolge unveränderbarer Bestandteil (readOnly) einer Überleitung und eines Seitensatzes sein kann (und nicht im Bild: auch einer Schlussgruppe und einer Durchführung). Dabei ist es nicht ausgeschlossen, dass weitere Eigenschaftswerte sich gleichen können (z.B. der Eigenschaftswert ›struktureller Terzzug‹). In diesem Fall skizziert das Modelldiagramm das herkömmliche Verständnis eines Satzmodells.[27]
Beispiel 12: UML-Diagramm zum Design eines Modells, das sich vom herkömmlichen Verständnis eines Satzmodells unterscheidet
In Beispiel 12 ist dagegen zu sehen, dass auch die Formfunktion eines Modells für eine Untersuchung konstant gehalten werden kann. Eine Analyse der Seitensätze der Sonaten KV 279 (189d) und KV 330 (300h) zeigt beispielsweise, dass die Fonte-Sequenz und I-x-V-I-Pendelharmonik (das ›Schema‹ in der Terminologie Robert Gjerdingens)[28] funktional äquivalent sind und praktische Substitutionsmöglichkeiten für die Gestaltung dieser Formfunktion bieten. Die genannten Harmoniefolgen sind also verschiedene Objektzustände des Modells ›Seitensatz‹ und es dürfte für ein konventionelles Denken in Satzmodellen irritierend sein, dass nicht durch Ableitung ineinander überführbare Harmoniefolgen das gleiche Modell repräsentieren können.
Anmerkungen
Dahlhaus 2001/GS3. | |
Zur Rezeption der Satzmodelle in Deutschland vgl. auch Froebe 2007 und Aerts 2007. | |
Dahlhaus (2001/GS3, 99) hat den Namen hierfür geprägt, indem er im Zusammenhang mit den Tanzmodellen ›Passamezzo‹ und ›Follia‹ von einem ›Parallelismus‹ der Klänge (g-B = T-Tp und B-F = Tp-Dp) gesprochen hat. Der Bezug zur Funktionstheorie in seiner Begründung lässt vermuten, dass die Bezeichnung Parallelismus im Hinblick auf Parallelklänge der Funktionstheorie gewählt worden ist. Carl Dahlhaus erwähnt darüber hinaus, dass der Parallelismus in Musik des 16./17. Jh. nur »vorgeformt« und seine Interpretation als Akkordsatz fragwürdig sei. Eine andere (von Dahlhaus wahrscheinlich nicht intendierte) Möglichkeit bestünde darin, den Namen Parallelismus auf den Intervallsatz (Terz-, Sextparallelen) des Satzmodells zu beziehen (vgl. Kaiser 1998, Bd. I, 177). Hierdurch ergibt sich zwar eine terminologische Unschärfe zu anderen Parallelismen (Quint-, Quart- und Sekundparallelismen), für die jedoch andere Bezeichnungen im Gebrauch sind (Mixtur, Fauxbourdon, Quint- und Quartorgana etc.). Abschließend sei angemerkt, dass in der Regel die Unschärfe, die der Bezeichnung ›Parallelismus‹ anhaftet, weder den wissenschaftlichen noch den praktischen Umgang mit dem Satzmodell behindert. | |
»Hiermit ist zunächst die Abstraktion von lebensweltlichen Sachverhalten und die Reduktion von Komplexität als Bedingung des Aufbaus der Eigenkomplexität eines Funktionssystems betont.« (Luhmann 1994, 112) | |
Luhmann 1992, 409. | |
Vgl. Koch 1793, §. 129., 342f. | |
Vgl. hierzu Kaiser 2009, 371–372. | |
Vgl. Krebs 1998. | |
In seinem Beitrag Von der Oktavzugmusik zur Terzzugmusik: Die Salzburger Notenbuchtradition und die Geschichte der Ursatz-Tonalität versucht Stefan Rohringer, die Schichtenlehre Heinrich Schenkers auf Luhmanns Systemtheorie zu beziehen. In diesem Zusammenhang wird behauptet: »Durch den Hinweis auf wie auch immer geartete Oktavregeln ist der Versuch einer funktionalen Einordnung der tonalen Verfahren aus der Perspektive der Schichtenlehre Schenkers (oder eines anderen Ansatzes) noch nicht überflüssig gemacht. Oktavregeln bilden kein funktionales System im Sinne der systematischen Entwürfe Riemanns, Schenkers oder Simons, sondern sind ein didaktisches Modell […].« (2010, 246) Bei der Reduktion der Oktavregel auf ein »didaktisches Modell« übersieht Stefan Rohringer, dass es gerade über den Funktionalismus nach Niklas Luhmann möglich ist, die Oktavregel gegenüber anderen theoretischen Entwürfen als gleichberechtigt zu behandeln. Nach Luhmann ist eine Funktion eine Regel, »nach der sich entscheiden läßt, durch welche Einsatzwerte (›Argumente‹) der Satz vervollständigt werden kann, ohne daß sein Wahrheitswert sich ändert. […] Die Klasse aller funktional äquivalenten Möglichkeiten wird gemeinhin als Variable bezeichnet. Variablen sind Begriffe, die planmäßig unbestimmt bleiben; sie sind Leerstellen, die aber nicht beliebig, sondern nur in bestimmter Weise, durch begrenzte Möglichkeiten ausgefüllt werden können. Die Variable ist durch einen funktionalen Bezugsgesichtspunkt definiert, an Hand dessen sich entscheiden läßt, welche Möglichkeiten der Ausfüllung in Betracht kommen, und der als Leitfaden zum Auffinden anderer Möglichkeiten führt.« (Luhmann 2009, 18) Luhmanns Funktionsbegriff lässt sich problemlos auf die Oktavregel übertragen: Eine Oktavregel wäre demnach funktionaler Bezugsgesichtspunkt, der Klassen funktional äquivalenter Harmoniefolgen bildet, anhand derer »sich entscheiden läßt, welche Möglichkeiten der Ausfüllung in Betracht kommen, und der als Leitfaden zum Auffinden anderer Möglichkeiten führt«. Auf der Grundlage eines solchen Funktionsbegriffs ist die Oktavregel nicht weniger ›funktional‹ als die Schichtenlehre Schenkers und Funktionstheorie Riemanns. Daher werden Oktavregel und Schichtenlehre im Folgenden als gleichwertig angesehen und die Tonleiter – unabhängig davon, aus welchem Diskurs auf sie verwiesen wird – als Metamodell zur Bestimmung der Formfunktion von Satzmodellen interpretiert. | |
Schenker 1956, 127. | |
Ebd., Figur 95e 3. | |
Zu weiteren Harmonisierungen vgl. Kaiser 2009 sowie eine Weiterführung des Forschungsprojekts im Internet: http://mozartforschung.de/transition/ | |
Vgl. hierzu Kaiser 2007, 259–262. | |
Die beiden Stimmen der Tonleiter sind dabei als Strukturstimmen, nicht als reale Sopran- und Bassstimme zu interpretieren. | |
Zitiert nach der EA 1850, A. Diabelli & Co., Nachlass, Lfg. 47, 5, mit einem nicht-authentischen Klaviervorspiel. | |
Warren Kirkendale (1972) hat für dieses Satzmodell den Begriff ›L’Aria di fiorenza‹ vorgeschlagen. Seine Bezeichnung hat Eingang in einige Artikel der ersten Auflage der MGG gefunden (z.B. Tagliavini 1961, 1290 und Mischiati 1973, 304 [dort nur Verweis auf Kirkendale 1972 im Literaturverzeichnis]). Im BRM (1995) sowie im Register der zweiten Auflage der MGG (1999) lässt sich diese Modellbezeichnung nicht mehr nachweisen. | |
Weber 1922, 191. Darüber hinaus hat Max Weber angemerkt: »Lehnt der Historiker (im weitesten Sinne des Wortes) einen Formulierungsversuch eines solchen Idealtypus als ›theoretische Konstruktion‹, d.h. als für seinen konkreten Erkenntniszweck nicht tauglich oder entbehrlich, ab, so ist die Folge regelmäßig entweder, daß er, bewußt oder unbewußt, andere ähnliche ohne sprachliche Formulierung und logische Bearbeitung verwendet, oder daß er im Gebiet des unbestimmt ›Empfundenen‹ stecken bleibt.« (Ebd., 195) | |
Vgl. Gosset 1989, 49–56. | |
Dahlhaus 2001a/GS2, 45. | |
Der Idealtyp Entchen-Kinderlied eignet sich nicht nur zur Vermessung des Liedes von Franz Schubert, sondern für zahlreiche Dur-Stücke, die einen charakteristischen harmonischen Verlauf (I–V | V–I) aufweisen. Vgl. hierzu Kaiser 2005, 166. | |
»Den Charakter einer Wissenschaft, um den sie sich bemüht, erhält die Musiktheorie nicht dadurch, daß sie sich – befangen von dem Vorurteil, das immer Gleiche sei das einzig Wissenswürdige – als unveränderlich behauptet, sondern gerade umgekehrt erst dann, wenn sie die Prätention einer Begründung in der Natur preisgibt, sich als Dogmatik im Epochenstil erkennt und das Ziel jeder Dogmatik zu erreichen sucht, zwischen historischer Triftigkeit und systematischer Geschlossenheit zu vermitteln.« (Dahlhaus 2002/GS4, 653) | |
Dahlhaus 2001b/GS2, 610. | |
Vgl. Gerhardt 2001, 39. | |
Luhmann 1992, 406: »Begriffe für sich genommen sind daher noch keine Theorie. Theorien sind begrifflich formulierte Aussagen, eingeschlossen Aussagen über Begriffe, und dies auch dann, wenn sie keine empirische Referenz aufweisen.« | |
Ebd., 415: »Methoden haben kein anderes Ziel als: eine Entscheidung zwischen wahr und unwahr herbeizuführen. Sie sind, im Unterschied zu Theorien, also zunächst auf ein extrem reduziertes Problem angesetzt«. | |
Ebd., 403–404: »Die Regeln richtigen Entscheidens über wissenschaftliche Kommunikation sind entweder theoretischer oder methodischer Art. Der Vorteil dieser Doppelung liegt auf der Hand: Beide Arten von Programmen können unter wie immer willkürlichen und vorläufigen Limitierungen in Operation gesetzt werden, da jede Limitation von der anderen Seite der Unterscheidung her infrage gestellt und gegebenenfalls ausgewechselt werden kann. Limitationen ohne Limitation also! Die Theorien können ausgewechselt werden, je nachdem, was ihre methodische Überprüfung ergibt. Und die Methoden werden gewählt, korrigiert und gegebenenfalls weiterentwickelt je nach dem, was man zur Überprüfung von Theorien braucht, und je nach dem, welche Theorien den Voraussetzungen der Methoden (zum Beispiel: Kausalität) Plausibilität verleiht. Das System findet in jeder praktischen Situation Anhalt in Limitierung und fällt nie ins Leere. Aber es ist trotzdem nicht an dogmatische Setzungen oder ein für allemal akzeptierte limitative Bedingungen gebunden, sondern kann von den Methoden her Theorien und von den Theorien her Methoden auswechseln.« | |
Im Sinne Joseph Riepels läge nur für den konkreten Fall einer VI#-II-V-I-Sequenz das Modell ›Fonte‹ vor. Die bei Mozart in Durchführungen häufig anzutreffende Verschiebung dieser Sequenz im Quintenturm (z.B. III#-VI-II-V), die den Reprisenanschluss über einen Quintfall erlaubt, ließe sich dem gegenüber als ›erweitertes Fonte‹-Modell bezeichnen. Der Terminus ›Quintfallsequenz‹ wäre in diesem Sinne die Bezeichnung für ein stark generalisiertes Modell, das als Oberbegriff für jede Struktur oder Sequenz, deren Akkordfolgen sich über fallende Quinten im Fundament beschreiben lassen, verwendet werden kann. | |
Vgl. Gjerdingen 1988, 3–38. |
Literatur
Hans Aerts (2007), »›Modell‹ und ›Topos‹ in der deutschsprachigen Musiktheorie seit Riemann«, ZGMTH 4, Hildesheim u.a.: Olms, 143–158. http://www.gmth.de/zeitschrift/artikel/250.aspx
Dahlhaus, Carl (2001/GS3), »Untersuchungen über die Entstehung der harmonischen Tonalität (= Saarbrücker Studien zur Musikwissenschaft 2), in: –––, Alte Musik. Musiktheorie bis zum 17. Jahrhundert – 18. Jahrhundert (= Gesammelte Schriften 3), hg. von Hermann Danuser in Verbindung mit Hans-Joachim Hinrichsen und Tobias Plebuch, Laaber: Laaber, 11–307 [Erstdruck: Kassel u.a.: Bärenreiter 1967].
––– (2001/GS2), Allgemeine Theorie der Musik II. Kritik – Musiktheorie / Opern- und Librettotheorie – Musikwissenschaft (= Gesammelte Schriften 2), hg. von Hermann Danuser in Verbindung mit Hans-Joachim Hinrichsen und Tobias Plebuch, Laaber: Laaber.
––– (2001a/GS2), Analyse und Werturteil, in: ––– (2001/GS2), 11–76 [Erstdruck als: Analyse und Werturteil (Musikpädagogik. Forschung und Lehre 8), Mainz u.a.: Schott 1970].
––– (2001b/GS2), »Musikwissenschaft und Systematische Musikwissenschaft«, in: ––– 2001/GS2, 604–630 [Erstdruck als Kapitel II in: Systematische Musikwissenschaft (= Neues Handbuch der Musikwissenschaft 10), Laaber: Laaber 1982, 25–48].
––– (2002/GS4), »Die Musiktheorie im 18. und 19. Jahrhundert. Zweiter Teil. Deutschland«, in: 19. Jahrhundert I. Theorie / Ästhetik / Geschichte: Monographien (= Gesammelte Schriften 4), hg. von Hermann Danuser in Verbindung mit Hans-Joachim Hinrichsen und Tobias Plebuch, Laaber: Laaber, 411–658 [Erstdruck als: Geschichte der Musiktheorie 11, Darmstadt: Wissenschaftliche Buchgesellschaft 1989].
Froebe, Folker (2007), »Historisches Panoptikum der Satzmodelle«, ZGMTH 4, Hildesheim u.a.: Olms, 185–195. http://www.gmth.de/zeitschrift/artikel/244.aspx
Gerhardt, Uta (2001), Idealtypus. Zur methodologischen Begründung der modernen Soziologie, Frankfurt a.M.: Suhrkamp.
Gjerdingen, Robert O. (1988), A classic Turn of Phrase. Music and the Psychology of Convention, Philadelphia: University of Pennsylvania Press.
Gosset, Philip (1989), »Carl Dahlhaus and the ›Ideal Type‹«, 19th-Century Music 13, 49–56.
Kaiser, Ulrich (1998), Gehörbildung. Satzlehre, Improvisation, Höranalyse. Ein Lehrgang mit historischen Beispielen, 2 Bde. (= Bärenreiter Studienbücher Musik 10 und 11), jeweils mit Audio-CD und im Aufbaukurs mit einem Formkapitel von Hartmut Fladt, Kassel u.a.: Bärenreiter.
––– (2009), »Der Begriff der ›Überleitung‹ und die Musik Mozarts. Ein Beitrag zur Theorie der Sonatenhauptsatzform«, ZGMTH 6, Hildesheim u.a.: Olms, 341–383. http://www.gmth.de/zeitschrift/artikel/448.aspx
––– / Carsten Gerlitz (2005), Arrangieren und Instrumentieren. Barock bis Pop. Ein Lernprogramm mit CD-ROM, Kassel u.a.: Bärenreiter
Kirkendale, Warren (1972), L’Aria di Fiorenza id est Il Ballo del Gran Duca, Florenz: Leo S. Olschki.
Koch, Heinrich Christoph (1793), Versuch einer Anleitung zur Composition, Bd. 3, Leipzig: Adam Friedrich Böhme.
Krebs, Wolfgang (1998), »Zum Verhältnis von musikalischer Syntax und Höhepunktsgestaltung in der zweiten Hälfte des 19. Jahrhunderts«, Musiktheorie 13, 31–41.
Luhmann, Niklas (1992), Die Wissenschaft der Gesellschaft, Frankfurt a.M.: Suhrkamp.
––– (1994), Die Wirtschaft der Gesellschaft, Frankfurt a.M.: Suhrkamp.
Mischiati, Oscar (1973), Art. »Canali (Canale), Floriano«, in: MGG, hg. von Friedrich Blume, Bd. 15, 1289–90.
Rohringer, Stefan (2010), »Von der Oktavzugmusik zur Terzzugmusik: Die Salzburger Notenbuchtradition und die Geschichte der Ursatz-Tonalität«, in: Funktionale Analyse. Musik, Malerei, antike Literatur. Kolloquium Paris, Stuttgart 2007, hg. von Bernhard und Bruno Haas, Hildesheim u.a.: Olms, 203–260.
Schenker, Heinrich (1956), Der freie Satz (= Neue musikalische Theorien und Phantasien 3), 2. Aufl. hg. und bearbeitet von Oswald Jonas, Wien u.a.: Universal Edition.
Tagliavini, Luigi Ferdinando (1961), Art. »Milioni (Millioni), Pietro«, in: MGG, hg. von Friedrich Blume, Bd. 9, 304.
Weber, Max (1922), »Die ›Objektivität‹ sozialwissenschaftlicher und sozialpolitischer Erkenntnis« [1904], in: Max Weber: Gesammelte Aufsätze zur Wissenschaftslehre, Tübingen: Mohr-Siebeck, 146–214.
Hochschule für Musik und Theater München [University of Music and Theatre Munich]
Dieser Text erscheint im Open Access und ist lizenziert unter einer Creative Commons Namensnennung 4.0 International Lizenz.
This is an open access article licensed under a Creative Commons Attribution 4.0 International License.