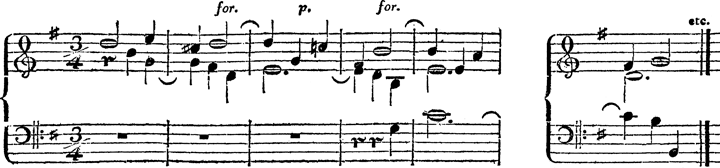Danuta Mirka, Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791, New York: Oxford University Press 2010

So klar wie der Titel der hier zu besprechenden Publikation auf den ersten Blick zu sein scheint – ›Metrische Manipulationen bei Haydn und Mozart‹ –, so sehr tauchen im Zuge der Lektüre des 332 Seiten starken Buchs Fragen über die tatsächliche Bedeutung des Ausdrucks ›Manipulation‹ auf. Neutrale Bedeutungen wie ›Handhabung‹ oder auch ›Kunstgriff‹ dürften ja nicht gemeint sein. Vielmehr scheint es um solche Eingriffe zu gehen, die das Metrum aus dem Gleichmaß bringen, die zu Irritationen des regelmäßigen Zeitflusses führen, die an ein ›Manipulieren‹ im Sinne ›rechtswidriger Beeinflussung‹ denken lassen, an gezielte Regelverstöße im Rahmen bestimmter ästhetischer Maximen also. Hierfür sprechen jedenfalls die Notenbeispiele, die ausnahmslos Phänomene zeigen, bei denen willentlich ›gegen‹ den Takt ›komponiert‹ – also ›manipuliert‹ wird.

So wie die Arbeit dann durchgeführt wird, hätte im Titel allerdings besser das Wort ›Unregelmäßigkeit‹ als ›Manipulation‹ gestanden. Denn die Verfasserin geht von den Ergebnissen der Manipulationen, nicht von diesen selbst aus. In den Hauptkapiteln ihrer Arbeit beschreibt und analysiert sie metrische Konstellationen, in denen der Takt bestätigt oder attackiert wird (3. Kap. »Sustaining Meter – Challenging Meter«), eine Phrasenstruktur in Verwirrung (›Imbroglio‹) gerät (4. Kap. »Changing Meter I: Change of Period«), einzelne oder mehrere Akzente den metrischen Gewichten widersprechen (5. Kap. »Changing Meter II: Change of Phrase«) oder gar latente, nicht notierte Taktwechsel zu verzeichnen sind (6. Kap. »Changing Meter III: Change of Tactus«). Nur im 2. Kap., das den Titel »Finding Meter« (übersetzt etwa: Auf der Suche nach dem Metrum) trägt, werden einige der Mittel angeführt, die man braucht, um in den zeitlichen Fluss – also auch ins metrische Gleichmaß – eingreifen zu können: Betonungsakzente, Längenakzente, diastematische Akzente (hier irrtümlich als ›pitch‹ bezeichnet[1]), harmonischer Wechsel, Mehrschichtigkeit (›streams‹), Bassführung und Kadenzbildung.

Die Verfasserin erweist sich als eine hervorragende Kennerin des Repertoires, das sie zeitlich und sachlich strikt eingegrenzt hat: fünf Jahre Wiener Klassik (1787 bis 1791), zwei Komponisten (Haydn und Mozart in ihren reifen Jahren) und ausschließlich Streicherkammermusik (Trio, Quartett, Quintett). Wem diese Eingrenzung als zu eng erscheint, der wird staunen, wie vielfältig und zahlreich die Fälle unregelmäßiger Zeitorganisation in diesen knapp 30 Werken sind. In gut 150 Beispielen mit meist kurzen Ausschnitten aus Partituren (bzw. auch aus zeitgenössischen Lehrbüchern) werden dem (Noten-)Leser immer wieder andere Klangszenen vorgeführt, in deren Verfolg er die metrische Orientierung zu verlieren droht. Riepel, Koch und andere gebrauchten für diese Verwirrspiele das italienische Wort ›Imbroglio‹. Allerdings haben sie nicht dessen Grenzen oder auch Prinzipien genauer bestimmt. So führte Heinrich Christoph Koch in seinem Musikalischen Lexikon als Beispiel für ›Imbroglio‹ zwar eine Stelle aus einem Streichquartett von Haydn an, blieb aber in der Beschreibung von dessen ›verwirrter‹ Struktur sehr vage: »So benennet man zuweilen diejenigen Sätze eines Tonstückes, in welchen eine entgegengesetzte Taktart eingemischt ist, wie z B. in folgendem Trio einer Menuet von Haydn« (Bsp. 1):[2]

Beispiel 1: Joseph Haydn, Streichquartett G-Dur op. 9/3, Menuett; Anfang des Trios, Wiedergabe bei Heinrich Christoph Koch[3]

Welche »entgegengesetzte« Taktart ist gemeint? Koch gibt darauf keine Antwort, und auch die Verfasserin der vorliegenden Schrift, die das Beispiel ablichtet, geht nicht näher darauf ein. Dies mag damit zu tun haben, dass sie bei ihren Diskussionen der metrischen Verhältnisse auf die explizite Einbeziehung rhythmischer Gegebenheiten verzichtet.[4] Während sie über den Begriff Metrum in einem eigenen Kapitel handelt (Kap. 1: »Musical Meter between Composition and Perception«), bleibt der Begriff Rhythmus unerörtert. Es ist allerdings zu bedenken, ob Fragen zur Metrik ohne Einbeziehung der Rhythmik überhaupt sinnvoll angegangen werden können. Im Fall des von Koch zitierten Beispiels kommt man etwa zu dem Schluss, dass – unter Beachtung mehrerer Rhythmustypen – eine 3/2-Struktur vorübergehend installiert wird, und zwar in zwei Schichten, die gegeneinander um eine Halbe Note versetzt sind (Abb. 1):[5]

Abbildung 1: Joseph Haydn, Streichquartett G-Dur op. 9/3, Menuett, Anfang des Trios, Angabe dreier Komponentenrhythmen sowie der Takt- (3/4) und der ›Imbroglio-Struktur‹ (3/2), letztere zwischen 1. und 2. Stimme versetzt

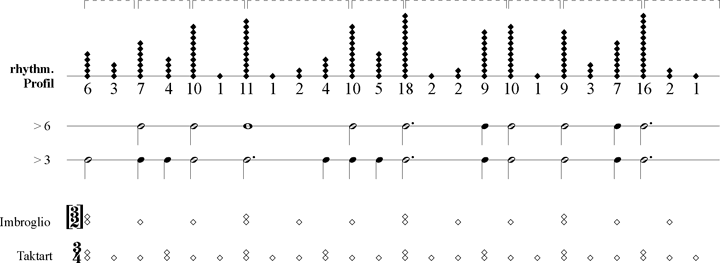
Koch hat in seinem Beispiel die Takte 7 und 8 weggelassen und somit auf die Auflösung des ›Imbroglio‹ verzichtet. Dabei scheint mir die Art, wie ein Komponist aus der Verwirrung wieder herausfindet, fast noch spannender zu sein, als diese selbst. Auch in der vorliegenden Schrift wird kaum einmal nach den Turbulenzen gefragt, die beim Wiedereintritt ins ruhige metrische Fahrwasser entstehen, vielmehr belässt Mirka es bei der Feststellung, dass sich durch die Überlagerung bzw. Verschiebung zweier Metren – hier eine 3/2-Struktur gegen die notierte 3/4-Struktur bzw. zwei gegeneinander versetzte 3/2-Strukturen – ›metrical dissonances‹ ergeben (133f.). Wiederum wird die Rhythmik ausgeklammert, mit der der Komponist aber letztlich das ›Imbroglio‹ gestaltet. Die relative Unordnung, die beim Übergang von einem metrischen Zustand in einen anderen herrscht, ist rein metrisch überhaupt nicht beschreibbar. Metrum kann als ein rhythmischer Sonderfall beschrieben werden: als ein Rhythmus, dessen Dauern gleich lang sind (bezogen auf die jeweilige metrische Ebene, versteht sich). Hieraus folgt aber, dass es notwendig des rhythmischen Geschehens und somit auch der rhythmischen Analyse bedarf, um Störungen in diesem Gleichmaß erfassen zu können. Erst das vielfältige rhythmische Gewebe eines Tonsatzes lässt die tatsächlich komponierten Gewichte hervortreten, die den zeitlichen Ablauf bestimmen und sowohl regelmäßig als auch unregelmäßig sein können. Es sei gestattet, die Gewichtsverhältnisse des vollständigen Achttakters von Haydn, der am Schluss ja vierstimmig wird, hier in Form eines ›rhythmischen Profils‹ mitzuteilen. Bei dessen Erstellung wurden nicht nur die oben verzeichneten drei Komponenten Klang, Diastematik und Dynamik, sondern sämtliche Klangereignisse, die für die Gliederung des Zeitflusses relevant sind (›Komponenten‹), einbezogen (nach englischer Terminologie: ›sound‹, ›contour‹, ›dynamics‹ and ›harmony‹) und – im Falle gemeinsamer Zeitpunkte – akkumuliert. Der anhand der Rhombustürme ablesbare ›Hauptrhythmus‹, der in zwei Gewichtsklassen ermittelt werden kann[6], zeigt anfangs binäre, teils auch dreifach binäre Anordnung, am Schluss aber zwei deutlich ternäre Takte.

Abbildung 2: Joseph Haydn, Streichquartett G-Dur op. 9/3, Menuett, Anfang des Trios, rhythmisches Profil T. 1–8 ermittelt aufgrund mehrerer Komponentenrhythmen und deren Akkumulierung[7]

Obgleich die Akzentverhältnisse der Taktarten – sei es der notierte 3/4- oder der komponierte 3/2-Takt, die hier nur als Schemen angedeutet sind – nicht in die Rechnung einbezogen wurden, tritt das Profil der entsprechenden metrischen Strukturen doch klar hervor (um es mit Christopher Hasty zu sagen: Meter ›as‹ Rhythm[8]). Noch wichtiger erscheint mir freilich, dass aufgrund der rhythmischen Analyse feinste Abstufungen unter den mit Gewicht belegten Zeitpunkten zu ermitteln sind, die in diesem Fall zwischen 1 und 18 Graden liegen, während bei konventioneller Taktanalyse nur zwei oder drei Gewichtsabstufungen (schwere Eins, leichte Zwei und Drei) gegeben sind.

Wenngleich die Verfasserin nicht über den Begriff Rhythmus handelt, benutzt sie ihn doch in verschiedenen Zusammenhängen. Bei Erörterung von Synkopen, die auch als »metrical displacement dissonances« (166) bezeichnet werden, tauchen Akzente, die auf leichte Taktteile fallen, als »chain of rhythmical dissonances« (ebd.) auf. Auch übernimmt die Verfasserin den Begriff »harmonic rhythm« (50), den Walter Piston[9] 1944 eingeführt und den Jan LaRue[10] 1957 auf Beethoven angewandt hatte. Doch weder im ersten noch im zweiten Fall verbindet sie den Begriff Rhythmus (oder rhythmisch) mit dem der Dauer, geschweige denn, dass sie in ihren Analysen Dauernfolgen unter die beobachteten Akzente bzw. Harmoniewechsel schreibt. So kann sie sich nicht von den vorgezeichneten Taktarten lösen, um auf so etwas wie ›Rhythm as Meter‹ zu stoßen. Akzente werden stets als Einzelereignisse auf ihre Lage im Takt hin befragt, desgleichen Harmoniewechsel wie auch Vorhalte oder Kadenzen, nicht aber in ihrer Eigenschaft als dauerngenerierende Ereignisse in die Analyse einbezogen. Sie setzt damit eine Gepflogenheit fort, die seit Lerdahls & Jackendoffs ›Metrical Well-Formedness Rules‹ und ›Metrical Preference Rules‹ sakrosankt zu sein scheint. Wie schon die Analysen der beiden Theoretiker zeigen, bleiben dabei allerdings zentrale musikalische Sachverhalte unerkannt. Der Anfang von Mozarts großer g-Moll-Sinfonie, den Lerdahl schon 1981[11] analysiert hat und auf den er zusammen mit Jackendoff in der ›Generativen Theorie der tonalen Musik‹ 1983[12] noch einmal zurückkam, erscheint denn auch als ein nichtssagendes Raster von hierarchisch geordneten Achtel, Viertel, Halben, Ganzen und Doppelganzen Noten. Die überaus prägnante und für diesen Sinfoniesatz spezifische Folge von sich verkürzenden Dauern bleibt dagegen unerwähnt (bei Mirka: 244). Schon der harmonische Rhythmus der ersten 22 Takte allein genommen zeigt das folgende charakteristische Rhythmusbild: 16 + 8 + 8 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 2 + 2 + 2 + 2 + 2 + 2 + 1 + 1 + 1 + 1 + 8 + 8 Viertel (usw.)

Die Analysemethode der Verfasserin ist nicht innovativ, die Beispiele für verschiedenste ›Imbroglios‹ gefunden zu haben, bleibt aber als ihre eminente Leistung bestehen. Hätte sie sich für rhythmische Fragen geöffnet, wären auch ihre metrischen Befunde noch klarer darzustellen gewesen. Z.B. die rhythmisch-metrischen Verhältnisse im Finale des f-Moll-Quartetts von Haydn (op. 55/2): Sie wären in ihrer außerordentlichen Kühnheit besser zu beschreiben, wenn die Dauernverhältnisse und nicht nur die Lage von Akzenten im Takt beachtet würden. Mit Bezug auf die Takte 60–63 weist die Verfasserin auf die korrespondierenden Viertel Noten a², es² und a¹ hin, die jeweils auf verschiedenen Taktteilen lägen (3., 4. und 1. Achtel) und zudem durch sforzato-Akzente (und übrigens auch durch ihre diastematische Lage) verstärkt würden. Dabei liegt das wirklich Verstörende des rhythmisch-metrischen Flusses an dieser Stelle in dem Umstand, dass hier – unter den Bedingungen des 6/8-Takts – 7-Achtel- und 9-Achtel-Phrasen gebildet werden (vgl. bei Mirka 288ff.). Dies ist der Verfasserin nicht aufgefallen, weil sie offenbar nicht auf Dauern, sondern stets nur auf Gewichte achtet.