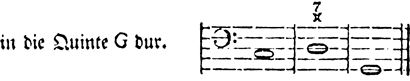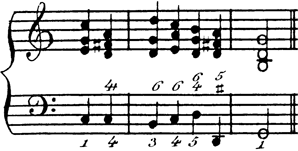Gedanken zu einer anderen Modulationslehre

Start: A-Dur, Ziel: Es-Dur, über: den neapolitanischen Sextakkord – klick – die Route wird berechnet…

Die Zielsetzung der Modulationslehre in den Lehrbüchern seit dem späten 19. Jahrhundert lässt an die Anforderungen denken, die an digitale Routenplaner gestellt werden: Unter Vorgabe einer Fortbewegungsart (vierstimmige Kadenz) soll über eine bestimmte Zwischenstation (Umdeutungsakkord) der schnellstmögliche Weg vom Ort A (Ausgangstonart) zum Ort B (Zieltonart) gefunden werden.

Was soll mit einer solchen Aufgabenstellung erreicht werden?

Doris Geller nennt in ihrer Modulationslehre (2002) als »höheres Ziel«[1] eine Art Training auf dem Gebiet der Harmonielehre: »Wer sich mit Modulation beschäftigt, übt sich in praktischer Harmonielehre.«[2] Ähnlich betrachten auch andere Autoren die Modulationslehre als Übungsmaterial zur Vertiefung harmonischer Kenntnisse, etwa Wilhelm Maler, der mit seinen Modulationsaufgaben die Absicht verfolgt, »die Vergegenwärtigung des Akkordmaterials der Tonarten zu beschleunigen und die Vorstellung von den tonalen Zusammenhängen zu schärfen.«[3] Unbestritten wird sich jemand, der eine derartige Modulationslehre durchgearbeitet hat, hinterher im Dickicht der Tonarten, Akkorde und enharmonischen Umdeutungen besser zurechtfinden. Kann dies aber tatsächlich ›höheres Ziel‹ der Modulationslehre sein?

Wird sie lediglich als ›Mittel zum Zweck‹ betrachtet, wird Modulation von ihrer musikalischen Bedeutung völlig losgelöst und zum bloßen Übungsstoff degradiert. Alles, was das Wesen einer Modulation in der Musik ausmacht – ihre klangliche Wirkung, ihre Ausdruckskraft, ihre formale Bedeutung etc. –, bleibt außen vor. Damit soll nicht gesagt werden, dass Kadenzübungen vollkommen aus dem Unterricht zu verbannen sind – im Gegenteil: Das ›Be-greifen‹ im Sinne des eigenen Tuns am Instrument oder auf dem Papier ist unentbehrlicher Bestandteil des Musiktheorieunterrichts. Zum Verständnis der Struktur und des Ausdrucksgehalts von Modulationen in der Musikliteratur wird eine mechanische ›Routenplanung‹ zwischen zwei Tonarten jedoch wenig beitragen können. Aufgaben, die Verständnis leisten wollen, müssen mit Musik in direkter Beziehung stehen und die tatsächliche Kompositionspraxis in irgendeiner Form widerspiegeln.

Einige Gedanken zu einer Modulationslehre, die nicht von vierstimmigen Kadenzübungen, sondern von der Musik selbst ausgeht, seien im Folgenden skizziert.

1. Modulation musikbezogen unterrichten

Die Forderung scheint selbstverständlich – sie ist es angesichts der verbreiteten Lehrpraxis aber offenbar noch immer nicht.[4] Die allermeisten Lehrwerke vermitteln Modulation mithilfe vierstimmiger Kadenzen oder durch Stufen- oder Funktionssymbole dargestellter Akkordfolgen; Literaturbeispiele werden entweder nachgeliefert oder fehlen ganz. Dafür werden gewöhnlich zwei Begründungen angeführt: einmal die Brauchbarkeit als Übungsstoff; zum anderen sollen Kadenzbeispiele »die harmonischen Vorgänge […] modellhaft nachbilden«[5] und somit »exemplarischen Charakter«[6] haben.

In der Satzlehre von Salmen/Schneider (1987) – die ansonsten erfreulicherweise sehr viele Musikbeispiele enthält – wird die Modulation in die Quinttonart in Dur lediglich durch eine Kadenz veranschaulicht:

Beispiel 1: Walter Salmen und Norbert J. Schneider, Der musikalische Satz. Ein Handbuch zum Lernen und Lehren (1987), 168

Betrachten wir denselben Modulationsweg (C-Dur → G-Dur) beim Übergang zum Seitensatz in Haydns Klaviersonate C-Dur Hob. XVI:35, 1. Satz:

Beispiel 2: Joseph Haydn, Klaviersonate C-Dur Hob. XVI:35, 1. Satz, T. 23ff.

Auf die Ausgangstonika C-Dur folgt – wie in Takt 3 der Beispielkadenz, allerdings bei Haydn als Sekundakkord – die Dominante zur Zieltonart (T. 23). Die Funktionstheorie würde in Takt 23 eine Umdeutung der Tonika zur Subdominante konstatieren.

Der funktionstheoretisch gesehen gleiche Vorgang findet sich im dritten Satz aus Haydns Klaviersonate Es-Dur Hob. XVI:49:

Beispiel 3: Joseph Haydn, Klaviersonate Es-Dur Hob. XVI:49, 3. Satz, T. 25–35

An die Tonika Es-Dur (als Sextakkord, T. 27/28) schließt sich der dominantische Quintsextakkord zur Quinttonart B-Dur an (T. 29), Umdeutungsakkord wäre auch hier die Tonika, die zur neuen Subdominante wird.

Schneiders Beispielkadenz kann aus der Perspektive der Funktionstheorie als Abstraktion des Modulationsvorgangs beider Haydn-Beispiele angesehen werden (T = S) – und doch verschweigt sie, dass die beiden Übergänge grundverschieden sind: In Hob. XVI:35 wirkt die Modulation durch dichte Führung der Außenstimmen und motivische Einheitlichkeit bruchlos und fließend, beinahe unmerklich wird der Hörer in die neue Tonart geleitet. Verbindende Funktion kommt dem c¹ der Unterstimme zu: Zunächst Grundton der Ausgangstonika, wird es am Ende von Takt 23 zur Dissonanz, die sich in die Terz der neuen Tonika auflöst. Im Gegensatz zu diesem nahtlos in den musikalischen Fluss eingebetteten Übergang setzt Haydn in Hob. XVI:49 die neue Dominante durch plötzliche Registerweitung, dynamische Markierung und motivischen Kontrast als deutlichen Umschlagspunkt.

Ist es einem Studierenden nicht zuzutrauen, eine Modulation von C-Dur nach G-Dur an einem Musikbeispiel nachzuvollziehen? Die beiden Stellen könnte man zunächst (in etwas größerem Zusammenhang als hier dargestellt) ohne Noten hören; im ersten Beispiel ist es schwieriger, den Zeitpunkt der Modulation auf Anhieb zu bestimmen, im zweiten ist der harmonische Wendepunkt für jeden deutlich wahrzunehmen. Die Gründe hierfür können anschließend untersucht werden, indem die Außenstimmen auf dem Klavier gespielt und Stimmführung, Motivik und Dynamik analysiert werden. Die beiden Modulationsbeispiele machen zwei grundsätzliche Gestaltungsprinzipien von Tonartenübergängen erfahrbar: das Trennende und das Verbindende – zwei Pole, zwischen denen sich jede Modulation bewegt und deren Analyse direkt zu den Ursachen für ihre musikalische Wirkung führt.

Es ist denkbar, anschließend die Beispielkadenz vorzulegen und kritisch zu prüfen, inwieweit sie die Modulationen darstellen kann und welche Gesichtspunkte sie nicht erfasst. Rasch wird so einsichtig: Bei Modulationen geht es nicht in erster Linie darum, die Zieltonart durch einen bestimmten (Umdeutungs-)Mechanismus möglichst schnell zu erreichen – es geht um den Weg dorthin und um alle musikalischen Mittel, die am Modulationsvorgang beteiligt sind.

2. Modulation integrativ unterrichten

Modulation ist ein in der Kompositionsgeschichte dur-moll-tonaler Musik nahezu allgegenwärtiges Phänomen. Es macht wenig Sinn, ein so umfassendes und facettenreiches Thema gesondert in zwei oder drei Unterrichtsstunden abzuhandeln. Bei einem Studenten, der innerhalb kürzester Zeit mittels Diatonik, Enharmonik und Chromatik durch alle Tonarten gejagt wird, bleibt statt des beabsichtigten Überblicks wohl eher ein Gefühl der Überforderung zurück; überdies läuft man durch eine zu komprimierte Darstellung Gefahr, komplexe Vorgänge soweit zu reduzieren und zu vereinfachen, dass jegliche Differenzierung verloren geht.

Sinnvoller ist es, Modulation als integrativen Bestandteil des Musiktheorieunterrichts an verschiedenen Stellen immer wieder zu thematisieren: Bei der Analyse barocker Suitensätze können Standardformeln, mit denen andere Kadenzstufen erreicht werden, untersucht werden, in Sonatensätzen lässt sich der Übergang zum zweiten Thema oder die Durchführungsharmonik analysieren, in Schubert-Liedern die subtile Verknüpfung von Tonartenübergängen und Textbedeutung. So kann auch historisch differenziert vorgegangen werden.

›Integrativ‹ soll aber auch heißen, dass man sich in verschiedenen theoretischen Disziplinen wie Harmonielehre, Kontrapunkt, Formenlehre und Gehörbildung – so sie denn getrennt unterrichtet werden müssen – mit Modulationen beschäftigt. Die Aufmerksamkeit kann so auf verschiedene Aspekte wie etwa Harmonik, Stimmführung, Klanglichkeit oder formale Funktion gerichtet werden.

Werden Modulationswege immer wieder in verschiedenen Zusammenhängen untersucht, bekommen die Studierenden Gelegenheit, Gesetzmäßigkeiten in unterschiedlichen Stilen, Formen und Epochen selbst zu entdecken; nach und nach gewinnt der Begriff ›Modulation‹ an Bedeutung. Auf diese Weise entsteht kein Schubladendenken, und das Vorsetzen fragwürdiger ›Modulationsrezepte‹ wird hinfällig.

3. Vom Gewöhnlichen zum Besonderen

Die Fülle an Modulationen, die in den Werken des 19. Jahrhunderts geradezu explodiert, macht den Systematisierungsversuchen der Lehrbücher spürbar zu schaffen. Aus dem Wunsch heraus, alle nur denkbaren Möglichkeiten mit einer einzigen Systematik abzudecken, werden seitenweise Tabellen aufgestellt, die die Umdeutungsmöglichkeiten eines oder mehrerer Akkorde darstellen:

Beispiel 4: Reinhard Amon, Lexikon der Harmonielehre (2005), 175[7]

Tabellen dieser Art, die sich in Lehrbüchern großer Beliebtheit erfreuen, sind gewissermaßen Symptom eines Hauptproblems der gängigen Modulationslehre: der Reduktion jeglicher Modulationsvorgänge auf die Bestimmung eines beiden Tonarten gemeinsamen Umdeutungsakkordes.[8] Zudem entsteht durch solche Schemata ein sehr diffuses Bild von Modulation, implizieren sie doch eine gewisse Beliebigkeit: Modulationstabellen suggerieren, jede Modulation sei möglich und gleich häufig anzutreffen.

Wohl ebenfalls aus dem Anliegen heraus, Modulation in ihrer ganzen Bandbreite zu erfassen, resultiert die auffällige Präferenz für sehr komplizierte und in der Musikliteratur selten anzutreffende Modulationswege. Wilhelm Maler beginnt das Modulationskapitel seiner Harmonielehre mit einer Modulation von C-Dur nach H-Dur[9], Peter Michael Braun mit den Beispielen C-Dur → D-Dur und A-Dur → F-Dur[10], und in der MGG2 findet man unter dem Stichwort »Modulation« (Unterkapitel des Artikels »Harmonielehre«) an erster Stelle eine Kadenz, die von C-Dur nach B-Dur moduliert, gefolgt von einer Modulation von Es-Dur nach fis-Moll.[11] Die Einführung in die Modulationslehre mit einem Beispiel, in dem von C-Dur nach H-Dur moduliert wird, ist in etwa so sinnvoll wie die Einführung der Sonatensatzform anhand der Klaviersonate von Alban Berg: Weder ist sie methodisch sinnvoll noch historisch vertretbar Eine Darstellung, die einen Überblick über Modulationen in der kompositorischen Praxis dur-moll-tonaler Musik geben will, sollte selbstverständlich zunächst repräsentative Beispiele enthalten. Daher ist es nicht nur wichtig, dass mit Musikbeispielen gearbeitet wird, sondern auch welche ausgewählt und in welchem Kontext sie eingesetzt werden.

Thomas Krämer und Manfred Dings bringen in ihrem Lexikon Musiktheorie (2005) für die sechs Modulationskategorien, die sie in Erweiterung der üblichen Einteilung ›diatonisch-enharmonisch-chromatisch‹ vorstellen, ausschließlich Literaturbeispiele. Für die Modulation mit dem übermäßigen Quintsextakkord ist unter der Überschrift »chromatisch-enharmonisch«[12] folgender Ausschnitt aus dem letzten Satz von Beethovens Streichquartett G-Dur op. 18 Nr. 2 abgedruckt:

Beispiel 5: Thomas Krämer und Manfred Dings, Lexikon Musiktheorie (2005), 167; Analyse von Ludwig van Beethoven, Streichquartett G-Dur op. 18 Nr. 2, T. 229–238

In der knappen Darstellung eines Handlexikons ist es verzeihlich, dass auf die formale Situation nicht eingegangen wird; weniger verständlich ist, warum alle Vortragsanweisungen fehlen: die Dynamik (decrescendo bis zum pp in T. 234), die Fermate in Takt 234 und die Artikulation (staccato in T. 235ff.).

Die Modulation findet am Ende der Durchführung statt; in den Takten 215ff. erklingt der dominantische Orgelpunkt d im Cello, der auf die Reprise in der Grundtonart G-Dur vorbereitet. In den Takten 229ff. erklingt die halbschlusstypische b6-5-Wendung mit dem übermäßigen Quintsextakkord auf der erniedrigten 6. Stufe. Die Fermate wäre eigentlich auf dem D-Dur-Akkord zu erwarten, gleichsam als Doppelpunkt vor dem Einsatz der Reprise. Stattdessen hält die Musik auf dem übermäßigen Quintsextakkord inne (T. 234), der nun als Dominantseptakkord zu As-Dur interpretiert wird – Beethoven schreibt in Takt 234 des¹ statt cis¹ –, es öffnet sich unerwartet noch einmal ein anderer harmonischer Raum. Wenige Takte später wird er schon wieder verlassen, über den verminderten Septakkord gelangt Beethoven nach G-Dur, in Takt 245 erklingt der erwartete Dominantseptakkord und zwei Takte später beginnt die Reprise: ein sehr schönes Beispiel für die Modulation mit dem übermäßigen Quintsextakkord – wunderbar kann hier die enharmonische Umschreibung und die Ambiguität des Klanges (einerseits Doppeldominante, andererseits Zwischendominante zur neapolitanischen Tonart) gezeigt werden. Exemplarisch ist das Beispiel allerdings nicht: Sehr viel häufiger als die Umdeutung eines übermäßigen Quintsextakkordes zu einem Dominantseptakkord ist der umgekehrte Vorgang; in einer kurzen Darstellung müsste daher die Umdeutung der Dominantseptim zur übermäßigen Sexte vertreten sein, ein Beispiel wie das von Beethoven sollte zumindest entsprechend kommentiert werden.

Natürlich möchten wir gerne auf besondere, erstaunliche oder individuelle Beispiele aufmerksam machen – gerade diese sind es ja, deren Erfindungsreichtum uns begeistert, und die ein Thema wie Modulation so spannend machen. Um das Individuelle und Besondere zu erkennen, muss aber das Gewöhnliche bekannt sein: Ein Musiker, der sich zunächst ›exemplarisch‹ mit Modulationen von C-Dur nach B-Dur und von Es-Dur nach fis-Moll beschäftigt, wird einer Modulation wie der in Beethovens Streichquartett allenfalls mit einem Achselzucken begegnen.

4. Umgang mit Theorien

Ich habe kürzlich eine Gruppe von Studierenden die beiden Modulationen aus Haydns Hob. XVI:35 und Hob. XVI:49 (siehe oben) mit drei verschiedenen Theorien beschreiben lassen: Zunächst mit Kirnberger, der (wie im 18. Jahrhundert üblich) als ausschlaggebendes Moment das Ergreifen der neuen Dominante nennt: »Die Ausweichung wird […] dadurch vorbereitet, daß man in der Fortschreitung auf die Dominante des neuen Tones kömmt.«[13]

Beispiel 6: Johann Philipp Kirnberger, Die Kunst des reinen Satzes in der Musik, Bd. 1 (1776), 113

Entscheidender Akkord wäre im ersten Haydn-Beispiel demnach der Sekundakkord auf der vierten Zählzeit in Takt 23, im zweiten der Quintsextakkord in Takt 29.

Anschließend haben wir die beiden Ausschnitte aus dem Blickwinkel Emanuel Aloys Försters analysiert, der den Modulationsvorgang als »Mischung verschiedener Tonleitern«[14] im Sinne der regola dell’ottava beschreibt:

Beispiel 7: Emanuel Aloys Förster, 160 Noten-Beispiele zu Emanuel Aloys Förster’s Anleitung zum General-Baß gehörig (1858), 8

Wie das c in Försters Kadenzbeispiel ist in Haydns Hob. XVI:35 das c¹ in Takt 23 zunächst 1. Skalenstufe in C-Dur; erklingt über dem c¹ der Sekundakkord, so findet in diesem Moment ein Wechsel der »Tonleiter« statt, den man daran erkennt, dass der Sekundakkord in der Regel charakteristischer Akkord auf der 4. Skalenstufe ist. In Hob. XVI:49 wird die Skala in Takt 29 gewechselt: a ist 7. Bassstufe der Tonart B-Dur und wird üblicherweise mit dem Quintsextakkord harmonisiert.

Die dritte Analyse haben wir mit der funktionalen Modulationstheorie vorgenommen: Die Tonika wird zur Subdominante umgedeutet.

Auf die anschließend neutral gestellte Frage, welche Theorie ihrer Meinung nach die Musik am treffendsten beschreibt, war sich die Gruppe einig, dass Kirnbergers Beschreibung den Höreindruck im zweiten Haydn-Beispiel am unmittelbarsten wiedergibt. Försters Herangehensweise konnten die Studierenden aber ebenfalls gut nachvollziehen, vor allem bei der Beschreibung der Modulation in Hob. XVI:35. Auch der Ansatz der Funktionstheorie – das Suchen nach der Verbindung der Tonarten – erschien ihnen plausibel. Wir kamen zu dem Ergebnis, dass jede der drei Theorien von ihrem Standpunkt aus durchaus überzeugend jeweils auf einen Aspekt des Modulationsvorgangs hinweist, dass aber keine davon alle Facetten der Modulationen beschreiben kann.

Theorien ermöglichen uns, verschiedene Perspektiven einzunehmen und so auf Dinge zu stoßen, die wir sonst vielleicht nicht entdeckt hätten. Vor allem zeitgenössische Theorien sind in dieser Hinsicht von unschätzbarem Wert, da sie uns Einblicke in frühere Denkweisen gewähren und Kategorien an die Hand geben, die oft besser geeignet sind, die Musik ihrer Zeit adäquat zu beschreiben. Doch auch für die Arbeit mit historischen Quellen gilt: Keine Theorie ersetzt die Auseinandersetzung mit dem Kunstwerk an sich – eine Analyse kann von einer Theorie geprägt sein, muss aber immer über sie hinausgehen.

5. Methodisches

Zwei Erkenntnisse der Lernforschung sind meiner Meinung nach auch für Lehrende an Hochschulen nicht zu unterschätzen.

Erstens: Nur das, was durch eigenes Tun und Entdecken gelernt wird, wird so verinnerlicht, dass es auch eigenständig angewendet werden kann. Für den Unterricht bedeutet das konkret: So wenig wie möglich vorgeben, so viel wie möglich selbst erfahren, herausfinden und üben lassen. Dies ist mitunter nicht einfach und erfordert ein hohes Maß an Zurückhaltung seitens der Lehrperson. Die Versuchung, alles selbst zu erklären, ist groß, da so scheinbar Zeit gespart wird. Längerfristig aber bleiben Inhalte, die durch eigene Erfahrung gelernt wurden, besser im Gedächtnis und müssen nicht ständig wieder in Erinnerung gerufen werden. Unterricht bleibt natürlich immer ein mehr oder weniger vom Lehrenden gelenkter Prozess – Aufgabenstellungen sollten Denkprozesse jedoch nicht ersetzen, sondern sie in Gang setzen.

Zweitens: Ein Unterrichtsgegenstand sollte auf möglichst vielen verschiedenen Ebenen zugänglich gemacht werden. Musiktheorie bietet hierfür vielfältige Möglichkeiten: Musik kann man hören, spielen, singen, lesen, mit Worten (mündlich oder schriftlich) beschreiben, den Kompositionsvorgang mittels Satzübungen nachempfinden, aus verschiedenen theoretischen Perspektiven analysieren, etc. – und dies alles in unzähligen didaktischen und methodischen Varianten.

Ein Vorschlag für eine Unterrichtssequenz soll diese Vorstellung von einem zu selbständigem Denken anregenden, methodisch vielseitigen und unmittelbar auf Musik bezogenen Unterricht illustrieren. Thema ist die klangliche Identität von übermäßiger Sexte und kleiner Septime und deren Bedeutung für Modulationen in entferntere Tonarten; vorausgesetzt wird, dass der übermäßige Sext-, Quintsext- und Terzquartakkord in kadenziellem Zusammenhang schon bekannt ist.

Zunächst werden ›Nahtstellen‹, an denen ein Formteil auf der Dominante endet, gehört und analysiert. Diese harmonische Situation ist typisch für das Ende von Durchführungen klassischer Sonatensätze, wo der Halbschluss oft so inszeniert wird, dass eine deutliche Reprisenerwartung entsteht.

Besonders nachdrücklich wirkt der Halbschluss, wenn die Dominante durch einen Halbtonschritt im Bass erreicht wird (Stufenfolge b6-5) und ihr ein übermäßiger Sext-, Terzquart- oder Quintsextakkord vorausgeht (letzterer ist aus Gründen der Stimmführung weniger häufig):

Beispiel 8: Wolfgang Amadeus Mozart, Klaviersonate G-Dur KV 283, 3. Satz, T. 166–171, übermäßiger Sextakkord

Beispiel 9: Wolfgang Amadeus Mozart, Klaviersonate a-Moll KV 310, 1. Satz, T. 77–79, übermäßiger Terzquartakkord

Um die nach außen drängende Bewegungsenergie der übermäßigen Sexte spürbar zu machen, kann von geeigneten Beispielen ein Außenstimmengerüstsatz gesungen werden.

Nun wird eine Passage aus dem Ende der Durchführung eines Mozart-Streichquartetts vorgelegt:

Beispiel 10: Wolfgang Amadeus Mozart, Streichquartett D-Dur KV 499, 1. Satz (Allegretto), T. 125–131

Die Takte werden erst angehört, dann von den Studierenden – je nach Fähigkeiten vierstimmig oder nur Violine 1 und Cello – mehrmals auf dem Klavier gespielt. Danach wird die Aufgabe gestellt, den Satz weiterzuschreiben: Wie endet die Durchführung, wie könnte eine Reprise beginnen? Die Ergebnisse werden vorgespielt und diskutiert; erwartungsgemäß werden die meisten einen Halbschluss und einen Reprisenbeginn in Es-Dur schreiben.

Im Anschluss daran wird die Stelle im Original mehrmals gehört:

Beispiel 11: Wolfgang Amadeus Mozart, Streichquartett D-Dur KV 499, 1. Satz (Allegretto), T. 130–135

Anhand der Partitur sollen die Studierenden selbst überlegen, wie die Modulation ›funktioniert‹ (in solchen Unterrichtsphasen ist es oft fruchtbar, wenn die Gruppe zunächst die Gelegenheit bekommt, unter sich, ohne Kommentar der Lehrperson, zu diskutieren): Der Ton as wird zu gis umgeschrieben und ändert seine Auflösungsrichtung; aus der kleinen Septime wird eine übermäßige Sexte, aus dem Dominantseptakkord der übermäßige Quintsextakkord. Damit ändert sich auch die Funktion des Basstons: War er gerade noch 5. Stufe der Tonart Es-Dur, stellt er sich in Takt 134 als erniedrigte 6. Stufe von D-Dur heraus. Der Schritt vom f zum d in der Bratsche (T. 133) verhindert die offene Quintparallele, die ansonsten zwischen Bratsche und Cello entstehen würde.

Um sich den harmonischen Vorgang noch einmal bewusst zu machen, wird der Akkord herausgeschrieben und einmal als Dominantseptakkord (a), dann enharmonisch umgeschrieben als übermäßiger Quintsextakkord (b) aufgelöst. Dasselbe kann in anderer Lage (c) geübt und auf andere Stufen transponiert werden. Die Bedeutung der Enharmonik lässt sich am besten singend nachempfinden: Beim Spielen auf dem Klavier wird gleichzeitig die kleine Septime bzw. übermäßige Sexte und deren Auflösung mitgesungen.

Beispiel 12: Enharmonik in Wolfgang Amadeus Mozarts Streichquartett D-Dur KV 499, 1. Satz (Allegretto), T. 130ff.

Ein anderes Musikbeispiel verdeutlicht, dass die enharmonische Umdeutung nicht immer im Notentext erkennbar ist:

Beispiel 13: Wolfgang Amadeus Mozart, Streichquartett d-Moll KV 421, Menuett, T. 16–31

Mit dem Auftakt zu Takt 22 – einer rhythmischen Reminiszenz an das Menuett-Thema – beginnt eine Quintfallsequenz (E⁷-A⁷-D⁷-G⁷-C⁷-F⁷-B⁷). Die Stimmen sind paarweise imitatorisch aufeinander bezogen: Cello und Bratsche wechseln sich taktweise mit den Grundtönen der Dominantseptakkorde ab, die Violinen werden chromatisch abwärts geführt. In Takt 27 wird die Sequenz unterbrochen; statt sofort in den B⁷ zu gehen, löst sich der F⁷ zunächst in einen B-Dur-Dreiklang auf. Die erwartete Septime erklingt vermeintlich in Takt 28, allerdings schreibt Mozart da bereits gis¹ statt as¹. Obwohl der Akkord klanglich dem Dominantseptakkord gleicht, ahnt man schon vor der Auflösung den übermäßigen Quintsextakkord. Dazu trägt auch die Akkordlage mit dem gis¹ in der Oberstimme bei. Am Ende von Takt 28 nimmt Mozart wie in KV 499 das f aus dem Akkord, der übermäßige Quintsextakkord wird zum übermäßigen Sextakkord, der sich in die Dominante zu d-Moll auflöst. Auf den Halbschluss folgt die Reprise des Menuett-Themas.

Das Sequenzmodell lässt sich gut abstrahieren und auf dem Klavier spielen:

Beispiel 14: Wolfgang Amadeus Mozart, Streichquartett d-Moll KV 421, Menuett, T. 22ff., Harmonieauszug

Die Sequenz kann an beliebiger Stelle unterbrochen werden, indem jeweils die kleine Septime als übermäßige Sexte betrachtet und entsprechend aufgelöst wird, z.B.:

Beispiel 15: Unterbrechung des Satzmodells aus Mozarts KV 421 an verschiedenen Stellen

Von diesem Punkt aus lassen sich verschiedene Wege einschlagen: Passend wäre das Beispiel aus Beethovens op. 18 Nr. 2, wo die Modulation in der gleichen formalen Situation ›umgekehrt‹ stattfindet. Dabei könnte man nun auch deduktiv vorgehen: Aus der Überlegung heraus, dass der harmonische Vorgang ebenso in die andere Richtung funktionieren müsste, wird die Umdeutung des übermäßigen Quintsextakkordes zum Dominantseptakkord am Klavier ausprobiert – wodurch unterscheidet sich die Modulation von der zuerst eingeführten Version?

In Werken des 19. Jahrhunderts richtet sich dann die Aufmerksamkeit vor allem auf die klangliche Inszenierung der Modulation. In Schuberts Liedern sind dafür wunderschöne Beispiele zu finden, ebenso aber in seiner Instrumentalmusik:

Beispiel 16: Franz Schubert, Klaviersonate a-Moll D 537, 3. Satz, T. 88–96

Die Modulation verbindet wie in Mozarts KV 499 zwei Durtonarten im Sekundabstand (in KV 499: Es-Dur/D-Dur, bei Schubert F-Dur/E-Dur). Dennoch wirkt der Übergang hier überraschender, mit dem E-Dur-Klang in Takt 95 geht eine deutliche Aufhellung, gleichsam ein Gefühl des ›Auftauchens‹ einher. Um die Ursachen dafür herauszufinden, spiele man folgende Alternativversionen: Auflösung des Akkordes von Takt 94

1. in einen F-Dur-Klang,

2. in einen H-Dur-Akkord,

3. in den Vorhaltsquartsextakkord zu e-Moll.

* * *

Mit der historischen Ausrichtung der jüngeren Musiktheorie ist ein deutlicher Aufbruch zu spüren: Inhalte der traditionellen Harmonielehre werden zunehmend aufgearbeitet, festgefahrene Methoden in Frage gestellt.

Wünschenswert wäre, dass diese Entwicklung auch in der Modulationslehre konsequent aufgegriffen und das unsinnige Regelkorsett der funktionalen Modulationstheorie aufgebrochen würde. Eine Modulationslehre, die von Musikbeispielen ausgeht, die Modulation nicht auf Umdeutungsmechanismen einengt und die dazu anregt, Modulationswege in verschiedenen musikalischen Kontexten immer wieder neu zu entdecken, kommt ohne in sich geschlossenes Regelsystem, ohne unverrückbare Gesetze und Gebote aus; sie ermöglicht durch überlegte Auswahl von Beispielen, Methoden und Aufgaben, dass ein angemessenes und musikbezogenes Verständnis von ›Modulation‹ wachsen kann.