Zwischen theoretischer Strenge und Milde - Anmerkungen zu Fred Lerdahls Tonal Pitch Space, Oxford: Oxford University Press 2001

Die musiktheoretische Auseinandersetzung mit Fred Lerdahls Monographie Tonal Pitch Space (TPS) führt auf interessante offene Fragen, denen der vorliegende Text an zwei Beispielen nachgehen soll. Die Diskussion dreht sich um ausgewählte Bestandteile von Lerdahls Theoriebildung und deren Anwendung unter dem Aspekt ihrer Motivation: Warum werden bestimmte musiktheoretische Gegenstände betrachtet? Warum werden bestimmte Definitionen im Gegensatz zu anderen besonders streng gefaßt? Mit der Konzentration auf diese speziellen Gesichtspunkte ist der Text keine neutrale Buchbesprechung. Der folgende Abschnitt ist der Versuch einer Verortung von Lerdahls Untersuchungen. Die beiden weiteren Abschnitte widmen sich jeweils der (mitunter kontroversen) Fortschreibung von konkreten Argumentationen aus TPS zu Theorie und Analyse.

1. Von lauter Bäumen zum Wald

Mit seiner 2001 erschienenen Monographie Tonal Pitch Space (TPS) hat Fred Lerdahl eine umfangreiche Untersuchung vorgelegt, welche den 1983 gemeinsam mit Ray Jackendoff vorgestellten Ansatz der Generative Theory of Tonal Music (GTTM) konsequent erweitert. Die Konsequenz betrifft einerseits die Analogie zwischen den Ereignishierarchien der GTTM und den in TPS hinzukommenden Tonhierarchien und andererseits deren gegenseitige Bezogenheit in der Analyse.

In der GTTM sorgen Wohlgeformtheitsregeln in erster Instanz für bestimmte Formen der hierarchischen Organisation musikalischer Ereignisse, und Präferenzregeln helfen in zweiter Instanz bei der Auswahl bevorzugter Hierarchien aus einem Vorrat von zwar möglichen – weil wohlgeformten –, aber weniger plausiblen Analysen eines Musikstückes. Dieser Vorrat an prinzipiell wohlgeformten Ereignishierarchien hat als solcher keine theoretische Durchdringung erfahren. Angesichts der Baumstruktur dieser einzelnen Ereignishierarchien kann man deshalb einen beliebten ^[1] metaphorischen Satz heranziehen, um die Situation des Analytikers zu charakterisieren: ›Er sieht den Wald vor lauter Bäumen nicht.‹ Der ›Wald‹ der wohlgeformten Ereignishierarchien existiert schlicht nur als ›lauter Bäume‹, und lediglich Präferenzregeln helfen dem Analytiker, einzelne Bäume für stabiler zu halten als andere. Die Topographie dieses Waldes selbst hat keine musiktheoretische Bedeutung. In TPS ist die Situation nun anders. Die Tonhierarchien sind konfigurierbar, d. h. verschiedene konkrete Tonhierarchien sind Ausprägungen einer variablen Hierarchie, die Lerdahl »Basic Space« nennt, und es werden Distanzen zwischen deren Ausprägungen ermittelt, die ihrerseits dann für die Längenbestimmung harmonischer Pfade herangezogen werden. Bleibt man im obigen Bilde, bedeutet das systematische Studium von Distanzen zwischen den Tonhierarchien eine konzeptuelle Aufwertung des ›Waldes‹. ^[2] Die Konfigurationen des diatonischen »Basic Space« werden von Lerdahl im Lichte vieler anderer Ansätze genau untersucht und daraus dann Wohlgeformtheits- und Präferenzregeln für Tonhierarchien im allgemeinen abgeleitet. Dieses Vorgehen führt allerdings eine diskussionswürdige Situation herbei: Manche musiktheoretischen Ideen verbinden sich mit Wohlgeformtheitsregeln und werden streng gefordert. Sie sind also unabdingbar. Andere dagegen verbinden sich mit Präferenzregeln und sind nur wünschenswert. Diese Aufteilung musiktheoretischer Inhalte wird bei Lerdahl mit kognitiven Ansätzen motiviert.

Die gegenseitige Bezogenheit zwischen Ereignis- und Tonhierarchien läßt sich im Grunde als Spezialfall einer Interaktion von Syntagmatik und Paradigmatik im Sinne der allgemeinen Syntaktik auffassen, wenn man nämlich Ereignishierarchien als Syntagmen und konfigurierbare Tonhierarchien als Paradigmen auffaßt und zudem in Rechnung stellt, daß die Plausibilität einer Analyse erst in der Interaktion beider Beschreibungsebenen beurteilt werden kann. ^[3] Lerdahls eigene Orientierung ist allerdings weniger semiotisch, sondern eher durch jene bereits im Vorwort der GTTM vorgenommene Verortung der Musiktheorie als Teilgebiet der Psychologie gekennzeichnet. Erklärtes Ziel der Theoriebildung und der detaillierten Analyse von Musikstücken ist kognitive Adäquatheit, was so viel heißt wie: Vereinbarkeit mit Ansätzen und Modellen der kognitiven Psychologie.

Der intensive Austausch zwischen Musiktheorie und Psychologie ist für beide Disziplinen von großer Wichtigkeit. Jedoch besteht seitens der Musiktheorie kein Anlaß für derartige akademische Unterwerfungsgesten, die buchstäblich zur Aufgabe ihres autonomen Gegenstandsbereiches führen würden. ^[4] Was die Musiktheorie von der heutigen Psychologie unterscheidet und was sie mit der Semiologie teilweise verbindet, ist eine gewisse Freiheit beim Nachdenken über die eigenen Gegenstände und beim gedanklichen Experimentieren mit denselben.

2. Ontologische Trockenübungen zur Diatonik

Obwohl der Begriff der Diatonik zu den tragenden Säulen der praktischen Musiktheorie zählt, ist seine theoretische Fundierung unsicher und daher Gegenstand einer fortwährenden Suche. Da sich Lerdahl in TPS um die Integration mehrerer Theorieansätze bemüht, bildet sein Ansatz einen anregenden Ausgangspunkt für eine Debatte um die Diatonik und andere Bestandteile einer Theorie der harmonischen Tonalität. Für die folgende Diskussion sind zunächst jene Untersuchungen von Carol Krumhansl ^[5], Diana Deutsch und John Feroe ^[6] aus der Musikpsychologie sowie von Gerard Balzano ^[7], John Clough und Jack Douthett ^[8] aus der Musiktheorie von Interesse, auf die sich Lerdahl selbst bezieht. Es müssen aber auch Untersuchungen von Norman Carey und David Clampitt ^[9] zur Sprache kommen, die Lerdahl in TPS nicht zitiert. Letztere sind deshalb von besonderem Interesse, weil Carey und Clampitt den Terminus der Wohlgeformtheit anders als Lerdahl mit der Diatonik verbinden. Ich will aufzeigen, daß hier nicht nur eine zufällige Homonymie zweier verschiedener Begriffe vorliegt, sondern zwei alternative ontologische Auffassungen darüber, worum es bei der musiktheoretischen Auseinandersetzung mit der Diatonik geht: ein kleiner Universalienstreit, wenn man so will. Lerdahl kommt darin die Rolle des ›Ton-Nominalisten‹ zu, wogegen Carey und Clampitt als ›Transformations-Realisten‹ charakterisiert werden können.

Zur Einordnung von Lerdahls Tonhierarchien sollte zuvor klargestellt werden, daß seine Untersuchungen eine diachrone Achse beinhalten, d. h. die Tonhierarchien und deren Konfigurationen werden selbst als historisch veränderliche ›Räume‹ verstanden. Der diatonische ›Basic Space‹ ist darin nur ein Spezialfall einer wohlgeformten konfigurierbaren Tonhierarchie; gleichwohl ist er ein ›übermächtiger‹ Spezialfall. Um aber auch andere Fälle mit aufzunehmen, benutzt Lerdahl die oben angesprochene Unterscheidung zwischen Wohlgeformtheits- und Präferenzregeln.

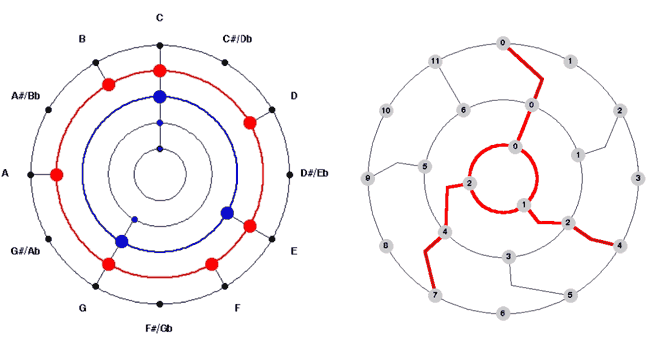
Die Annahme der hierarchischen Organisation ist durch die Interpretation experimentalpsychologischer Befunde motiviert. Einen wichtigen Anker bilden die von Carol Krumhansl experimentell gewonnenen Testton-Profile, welche die Dur- und Molltonarten in Form kontextbedingter quantifizierter Tonpräferenzen auf der Basis des Zwölftonsystems repräsentieren. ^[10] Solange man diese Profile direkt als Gegenstände einer statistischen Musiktheorie betrachtet (was in der Musikinformatik durchaus populär ist), können sie mitunter die traditionellen Gegenstände, wie Töne, Akkorde oder Skalen, ersetzen. Wenn man so will, ist Tonalität als statistischer Begriff dann nichts als eine systematische Störung der homogenen ›Atonalität‹. Der Begriff der Tonhierarchie kommt erst wieder ins Spiel, wenn man Krumhansl oder Deutsch und Feroe darin folgt, die statistischen Daten im Sinne bestimmter kognitiver Hypothesen zu deuten. Sowohl Krumhansl als auch Deutsch und Feroe interpretieren diese Profile als Überlagerungen dreier Ebenen: Als unterste fungiert das unveränderliche Zwölfhalbtonsystem. Darüber hat man eine variable diatonische Ebene und relativ zu dieser wiederum eine variable Dreiklangsebene. Bis auf zwei definitorische Feinheiten folgt Lerdahl dieser Auffassung. Sie lassen sich anhand der Gegenüberstellung in Abbildung 1 erläutern. Die fünf konzentrischen Kreise auf der linken Seite von Abb. 1 zeigen Lerdahls vollständige Tonhierarchie (›Basic Space‹) in einer Konfiguration, die den C-Dur-Dreiklang als eine Stufe der C-Diatonik beschreibt. Jeder der 7 Dreiklangsstufen in jeder der 12 diatonischen Skalen entspricht eine von 84 = 7 mal 12 möglichen Grundkonfigurationen: Bei fixierter äußerster (oder ›unterster‹) Ebene können die zweite und dritte Ebene entsprechend frei konfiguriert werden. Die beiden innersten (oder ›höchsten‹) Ebenen der Lerdahlschen Hierarchie sind indes nur scheinselbständig. Sie sind nicht frei konfigurierbar, sondern starr mit der Dreiklangsebene verbunden und kennzeichnen lediglich die Wichtigkeit von Grundton und Quinte innerhalb des Dreiklangs. ^[11]

Abbildung 1: Lerdahls Tonhierarchie (links) und Douthetts Stroboskop (rechts).

Sieht man von diesen innersten Ebenen ab, so unterscheidet sich die linke Hierarchie von der rechten (hier als Douthett-Stroboskop ^[12] bezeichneten) in weiteren Details. Den Wohlgeformtheitsregeln für Tonhierarchien gemäß, die Lerdahl allen Hierarchien auf seiner diachronen Achse auferlegt, sind die Konstituenten aller Ebenen ›pitch classes‹, und jede ›pitch class‹, die auf einer bestimmten Ebene auftritt, tritt auch auf allen darunter liegenden Ebenen auf. Das heißt, die Ebenen sind von innen nach außen streng ineinander enthalten. Die Tonhierarchie ist ein sukzessiver Filter. Im Douthett-Stroboskop dagegen sind alle drei (gegeneinander verschiebbaren) Ebenen gleichermaßen homogen. Darüberhinaus gibt es eine Modalität, von den beiden innen liegenden Ebenen aus in der je außen folgenden Ebene eine konfigurationsabhängige bestmögliche Gleichverteilung von ebenso vielen Tönen auszuwählen. Hinter jedem Ebenenwechsel verbirgt sich die begriffliche Unterscheidung zwischen generischen und spezifischen Intervallen. Lerdahl flirtet durchaus mit einer abgemilderten Auffassung, die von dieser Dichotomie inspiriert ist, ohne sie jedoch als Gegenstand der Theorie anzuerkennen. ^[13] Strenggenommen betrachtet er nur die je spezifische Seite, nicht aber die von Clough und Meyerson ^[14] bzw. Clough und Douthett ^[15] untersuchte Modalität ihres Zustandekommens aus der generischen. Hierin kommt Lerdahls Ton-Nominalismus zum Ausdruck. Die von Deutsch und Feroe betrachteten hierarchisch eingebetteten Alphabete erkennen den generischen Ebenen dagegen weit mehr Autonomie zu.

In den mathematisch-musiktheoretischen Untersuchungen von Carey und Clampitt ^[16] wird das transformationelle Zusammenspiel der generischen und spezifischen Beschreibungsebenen ins Zentrum der Untersuchungen gestellt. Ohne hier zu sehr ins Detail zu gehen, sollen die daraus ableitbaren ontologischen Konsequenzen verdeutlicht werden.

Clough und Meyerson ^[17] haben bereits auf wichtige Besonderheiten der Interaktion von generischen und spezifischen Intervallen hingewiesen. Insbesondere haben sie dabei die Eigenschaft der Generiertheit im Zusammenspiel mit anderen Eigenschaften studiert, die auch Lerdahl in der Liste seiner wünschenswerten Eigenschaften aufführt. Am Beispiel der spezifischen Diatonik im homogenen Zwölfhalbtonsystem meint Generiertheit die Möglichkeit, die sieben Töne als Quintenkette zu generieren: F–C–G–D–A–E–H.

Ausgehend vom Begriff der Generiertheit haben Carey und Clampitt nachgewiesen, daß sich die wesentlichen Bestandteile der diatonischen Theorie von Clough und Meyerson formulieren lassen, ohne von einer vorgegebenen homogenen Chromatik auszugehen. Zwar erachtet auch Lerdahl die inneren Ebenen als prominenter, aber in seinen Wohlgeformtheitsregeln beherrscht die äußere Ebene die inneren, weil sie diese enthält. Carey und Clampitt entwerfen hingegen eine Dynamik des Generierens von Tönen bzw. Tonsystemen, bei denen der Prozeß selbst von innen nach außen führt und den Akten des Generierens und Transformierens von Ebenen mehr Gewicht beimißt als den Tönen selbst. Wohlgeformtheit ist bei ihnen eine innere Transformationseigenschaft des generischen Systems und betrifft am Beispiel der Diatonik die wechselseitige Übersetzung von diatonischen Schritten in Quintschritte und umgekehrt.

Eine Schlüsselstelle für die weiterführende produktive Kritik von Lerdahls Ton-Nominalismus ist ein kurzer Abschnitt am Ende des 3. Kapitels »Paths in Pitch Space«. Unter Verweis auf die fundamentale Rolle von Orts-, Zeit- und Bewegungskategorien in Ray Jackendoffs ^[18] Untersuchungen zu Kognition und Semantik argumentiert Lerdahl zugunsten einer ebensolchen Rolle dieser Kategorien für die Kognition von Musik und macht dabei klar, daß er den Begriff der Bewegung im Sinne von Positionsveränderung im Tonraum bzw. im Raum der Tonhierarchien versteht. Damit baut er eine Brücke zu einem analogen Universalienstreit um den Bewegungsbegriff der Physik. Versteht man Bewegung als einen dynamischen Zusammenhang von Positionsveränderung, Impulsveränderung und Energie, dann wäre die einseitige Anerkennung von Positionsveränderungen eher nominalistisch zu nennen. Transformations-Realisten würden hingegen Bewegungen als Hamiltonsche Flüsse ansehen: als Familien von Transformationen eines Phasenraumes. ^[19]

3. Glaubensmotive auf Abwegen

Das mit dem Titel »Paths in Pitch Space« überschriebene 3. Kapitel dient Lerdahl zu freizügiger Erkundung des analytischen Potentials, welches das Modell der Tonhierarchien bereithält. Einen gesonderten Abschnitt von immerhin 15 Seiten ^[20] widmet er dabei einer Analyse von Richard Wagners Parsifal in Hinblick auf narrativ motivierte Pfade im Weberschen Netz der tonalen Regionen. Dazu wiederum veranlaßt ihn neben Wieland Wagners Deutung des Kreuzes als ›psychologisches Diagramm‹ in dessen Bayreuther Inszenierung von 1951 u. a. die Vermutung, daß Wagner selbst mit Gottfried Webers Versuch einer geordneten Theorie der Tonsetzkunst vertraut gewesen sein könnte (z. B. durch Austausch mit Robert Schumann, vgl. TPS S. 138). Die Ausdehnung des Tonnetzes in zwei Richtungen (Quint- und Kleinterz-Verwandtschaft) und die Tatsache, daß man in diesem Netz bei enharmonischer Verwechslung vier verschiedene Richtungen einschlagen kann, um von der (mit Parsifal assoziierten) Region D-Dur zur Region der Haupttonart As-Dur zu gelangen, ergeben eine Homomorphie zwischen dem Symbol des Kreuzes und einer narrativen Wanderkarte für die tonalen Regionen. Entsprechend widmet sich Lerdahl je vordringlich der Frage, ob ein harmonischer Pfad nach rechts ›zum Guten‹, nach links ›zum Bösen‹, nach unten ›zum Leid‹ oder nach oben ›zur Erlösung‹ führt. Diese Analyse soll hier nicht im einzelnen nachgezeichnet werden. Die meisten von Lerdahls Argumenten beziehen sich entweder auf ebendieses traditionelle Webersche Netz oder auf das mit der As-Dur-Region assoziierte lokale diatonische Netz, dem die gleiche Homomorphie unterlegt wird: diatonische Quintschritte als Vertikale und diatonische Terzschritte als Horizontale. Nur wenige beiläufig eingestreute Details nehmen tatsächlich Bezug auf Lerdahls hybriden Raum, der Stufen und Regionen im Zusammenhang betrachtet. Solange es nur um die Bestimmung der jeweiligen narrativen Richtungen geht – so könnte man argumentieren –, ist es ohnehin gleichgültig, ob sie anhand diatonischer, regionaler oder einer Vermischung beider Gesichtspunkte aufgezeigt werden.

Semantisch prominenter als die Unterscheidung von Regionen und Stufen ist die zwischen Diatonik und Chromatik. Fortschreitungen nach rechts (wie im Grals-Motiv) sind eher diatonisch. Fortschreitungen nach links (wie im Klingsor-Motiv) sind eher mit Chromatik durchsetzt. Im Grunde sind es die Richtungen des Fundamentalbasses, die ganz im Sinne Rameaus nach Quint- und Terzfortschreitungen bilanziert werden.

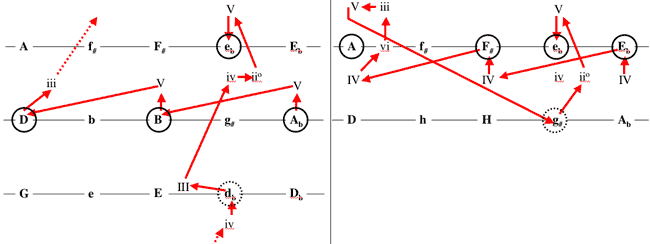
Aber gerade in Hinblick auf seine eigene Theorie der Regionen und Stufen läßt sich Lerdahl beim Parsifal eine Pointe entgehen. Die von ihm genauer analysierten Takte 45–55 des Vorspiels (siehe Notenbeispiel 1) nimmt Richard Cohn ^[21] zum Ausgangspunkt für eine alternative Interpretation dieser Takte im ›Lerdahl-Stil‹. Abbildung 2 zeigt die harmonischen Pfade im Vergleich.

Beispiel 1: Takte 45–55 des Vorspiels zu Parsifal.^[22]

Abbildung 2: Fred Lerdahl (links) und Richard Cohn (rechts) unterlegen die Takte 45–55 mit verschiedenen harmonischen Pfaden.

Hinsichtlich der Fortschreitungsrichtung der Takte 45–51 liefern beide Interpretationen denselben Befund: Das Glaubensmotiv wird in kleinen Terzen aufwärts transponiert, was harmonisch eine regionale Fortschreitung im Weber-Netz nach links ›zum Bösen‹ bedeutet. Lerdahl gibt folgende semantische Auslegung an: »The implication is that faith must confront and vanquish sin in order to recover the spear and hence the health of the society of the grail.«

Die harmonischen Pfade unterscheiden sich aber in der Deutung der Quartfälle As -> Es und Ces -> Ges als halbschlüssige Wendungen der Form I -> V in As-Dur und Ces-Dur (bei Lerdahl) bzw. als plagale Wendungen der Form IV -> I in Es-Dur und Ges-Dur (bei Cohn). Auf den ersten Blick hat Lerdahls Interpretation mehr Attraktivität. Sie stimmt auch mehr oder weniger mit David Lewins ^[23] Sicht überein. Lewin hält sogar noch eine Beobachtung bereit, die über eine bloße Kleinterz-Fortschreitung der Regionen nach links und damit über Lerdahls semantische Auslegung hinausgeht: Die regionalen Zentren As -> Ces -> D (oder Eses) -> Es bilden den Anstieg zum Zaubermotiv, wie es im entscheidenden Moment im zweiten Akt erklingt: Kundrys Kuß.

Teilt womöglich der Musiktheoretiker Amfortas Schicksal, wenn er sich von dieser Interpretation bezaubern läßt? Parsifal wird jedenfalls seine aktive Rolle im ganzen Geschehen klar, indem er sein ›törichtes‹ tonikales D als ein subdominantisches im As-Dur-Zusammenhang begreift. ^[24] Lewin ^[25] zeigt, daß drei Deutungen des D/Eses als Subdominante am Ende der Oper ineinander verschränkt werden: D als Hochalteration der Subdominante Des von As, Eses als subdominantischer Neapolitaner zu Des (und damit als intellektuelle Auflösung des ursprünglich auf D bezogenen trugschlüssig endenden Torenspruch-Rätsels) und Eses als sechsfache Subdominante zu As.

Cohns Interpretation der Takte 45–55 stellt einen Bezug zu diesem ›erlösenden‹ plagalen Modell her. Wagner selbst winkt in den Takten 46 und 49 mit dem Zaunpfahl: Pfundnoten, Fortissimo mit Diminuendo bis zum Piano und Paukenwirbel. Auch das vorangehende erweiterte Gralsmotiv (Takte 39–43, Notenbeispiel 2) läßt zwei Deutungen zu.

Beispiel 2: Erweitertes Gralsmotiv.

Sieht man von den Terzfortschreitungen im einzelnen ab, so ergeben sich bezogen auf As-Dur taktweise: I -> IV -> I – I -> V. Stellt man jedoch in Rechnung, daß die Takte 42 und 43 (Holzbläser) eine Imitation der Takte 40 und 41 (Blechbläser) sind, so liegt auch eine analogisierende harmonische Interpretation auf der Hand: IV -> I in As wird zu IV -> I in Es. Wagners Erweiterung des bereits von Mendelssohn in der Reformations-Sinfonie benutzten ›Dresdener Amens‹ könnte also insbesondere auf das Herstellen dieser Ambiguität zwischen V|I und I|V abzielen.

Lerdahls Theorie hält für solche Situationen das Prinzip des kürzesten Weges bereit, und im Zusammenhang mit der Parsifal-Analyse zieht Lerdahl dieses sogar selbst bei der Diskussion des Klingsor-Motivs heran. Im Falle der Takte 45–55 steht er aber offenbar zu sehr im Banne des Zaubermotivs, um an die eigene Theorie zu glauben. Ein vergleichender Blick auf die beiden Pfade in Abbildung 2 zeigt, daß Cohns ›Erlösung vorausahnende‹ Interpretation eine kürzere harmonische Wegbilanz aufweisen kann. Eine noch kürzere gibt es nicht. ^[26]