Die romantische Musik mit ihrer progressiven Harmonik hat die Musiktheorie zu vielen Deutungsvorschlägen angeregt. In der Nachfolge von Hugo Riemanns musiktheoretischen Konzepten entstand vor allem in Amerika in jüngerer Zeit eine Strömung, die inzwischen international etabliert ist und deren einzelne Ansätze unter dem Begriff Neo-Riemannian Theory (NRT) zusammengefasst werden. Die Methoden der NRT zeichnen sich nicht zuletzt durch die vielfältige Verwendung graphischer Modelle aus. Richard Cohn, dessen Arbeiten die NRT maßgeblich geprägt haben, erläutert in seinem 2012 erschienenen Buch Audacious Euphony – Chromaticism and the Triad’s Second Nature[1] verschiedene zu dieser Zeit bekannte Modell-Transformationen und kombiniert sie teilweise zu neuen, aussagekräftigeren Varianten. Im siebenten Kapitel widmet er sich den in der NRT unterrepräsentierten Vierklangsverbindungen. Der vorliegende Beitrag greift einige der in Audacious Euphony entwickelten Gedanken auf, skizziert deren Grundlagen und stellt einige neu entwickelte Modelle zur Deutung und Darstellung verschiedener Akkordverbindungen (Hexentreppe, Heart Cubes, Vierklangs-Spindel) sowie eine Erweiterung des 3D-Tonnetzes von Edward Gollin[2] vor, die sich größtenteils mit Vierklangs-Relationen befassen und deren Vorteil in einer dreidimensionalen Darstellungsweise liegt.

1. Hexentreppe

Grundlage der meisten Modelle der NRT ist das Tonnetz, ein – prinzipiell unendliches – zweidimensionales Raster aus gleichseitigen Dreiecken, das die Nachbarschaftsbeziehungen von Dur- und Molldreiklängen darstellt (Abb. 1).

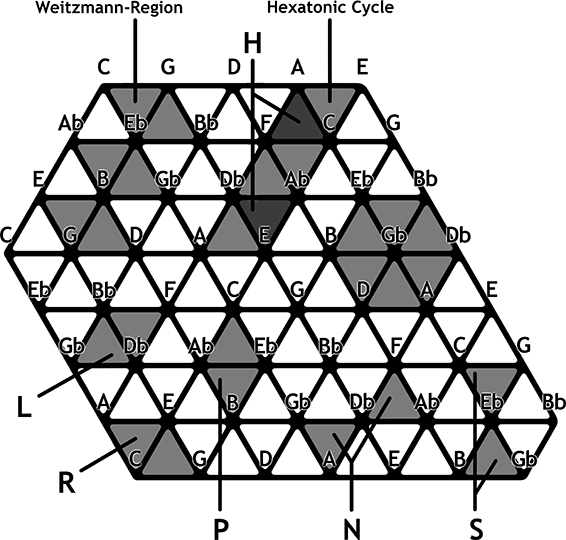
Abbildung 1: Ausschnitt aus dem Tonnetz

Seine drei Achsen sind in großen Terzen (bzw. in dem Komplementärintervall, in kleinen Sexten), kleinen Terzen (großen Sexten) und Quinten (Quarten) unterteilt. Jedem Schnittpunkt der drei Achsen ist eine Tonhöhe zugewiesen.[3] Es ergibt sich aus dieser Anordnung, dass jedes Dreieck im Verbund seiner Eckpunkte einen Dreiklang ergibt, aufwärts weisende Dreiecke immer Dur-Dreiklänge, auf der Spitze stehende immer in Moll-Dreiklänge. Ferner ist jeder einzelne Ton von jenen sechs Nachbartönen umgeben, die in einem Konsonanzverhältnis zu ihm stehen (nach klassischer Auffassung die obigen sechs Intervalle), sowie von ausschließlich jenen sechs konsonanten Dreiklängen, von denen er Bestandteil ist (im grauen Sechseck um Ges sind drei Dur- und drei Molldreiklänge enthalten). Im Tonnetz lassen sich verschiedene chord-relations als Verbindung zweier Dreiecke darstellen, beispielsweise P (parallel): As-Dur/as-moll, L (Leittonwechselklang): Ges-Dur/b-Moll, H (hexatonic pole): F-Dur/des-Moll, R (relative): C-Dur/a-Moll, N (nebenverwandt): Des-Dur/ges-Moll, S (slide): H-Dur/c-Moll.[4] Charakteristisch für diese Neo-Riemannian relations ist die chromatisch enge Stimmführung (Cohn nennt den Austausch eines einzelnen Tones, z. B. Ges-F in L einen flip um die gemeinsame Achse). L, P und H ergeben in Kombinationen nur Progressionen innerhalb der Grenzen eines hexatonic cycle (eine Gruppe von sechs Dreiklängen auf der hexatonischen Kleinsekund-Kleinterz-Skala), R, N und S bewegen sich in gleicher Weise in einer Weitzmann-region (eine vergleichbare Gruppe aus ebenfalls sechs Dreiklängen auf der oktatonischen Kleinsekund-Großsekund-Skala, benannt nach Carl Friedrich Weitzmann, der 1853 in seiner Schrift Der Uebermaessige Dreiklang[5] die ersten Anstöße in Richtung einer neuen Musiktheorie gab).

Zunächst will ich eine Alternative zum Cube Dance vorstellen, einem Modell, das aus einer algorithmischen Folge von Dreiklangsverbindungen konstruiert ist (Abb. 2). Cohn übernahm dieses Modell leicht verändert von Jack Douthett und Peter Steinbach.[6] Es vereint die beiden für seine Argumentation essentiellen Dreiklangsgruppen der Weitzmann-region[7] und des hexatonic cycle[8] zu einem Gebilde, das alle 24 Dur- und Molldreiklänge sowie die vier übermäßigen Dreiklänge in zwölf voice-leading zones unterteilt. An ihnen kann man die Stimmführungsdistanz zwischen den Dreiklängen in Halbtonschritten (Cohn nennt diese minimale Einheit chromatischer Stimmführung eine working unit) ablesen.

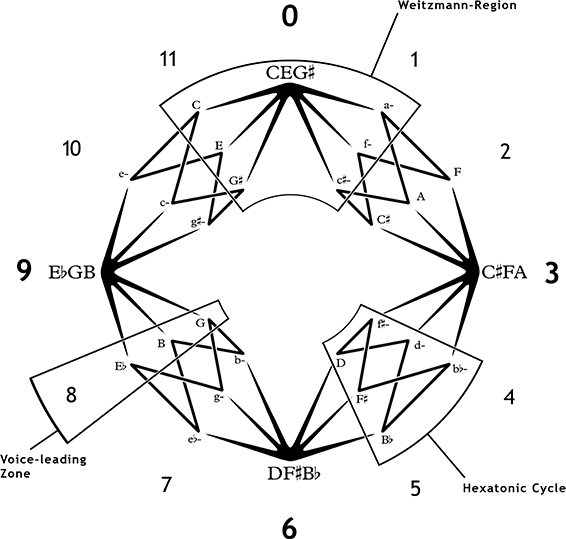
Abbildung 2: Cube Dance

In dem Modell sind die Dreiklänge zu Punkten zusammengezogen. Bei der eigenständigen graphischen Darstellung der Weitzmann-region ringt Cohn mit verschiedenen Fassungen, die sich schrittweise vom entsprechenden Ausschnitt des Tonnetzes entfernen (Abb. 3). Im Original ist der übermäßige Dreiklang durch drei Glieder der Großterzachse abgebildet und die region besteht aus den sechs anliegenden Dreiecken. Nachteilig an dieser Darstellungsweise sind die Umstände, dass erstens ein Ton des übermäßigen Dreiklangs verdoppelt wird und an beiden Enden der Achse auftaucht, zweitens dieser Akkord ein anderes Erscheinungsbild als die sechs umliegenden Akkorde hat und drittens die Stimmführungsdistanz von je zwei Halbtonschritten zwischen den sechs Dreiklängen nicht ablesbar ist. Das dritte Problem löst Cohn, indem er den übermäßigen Dreiklang zu einer Fläche aufspreizt, an der die sechs Akkorde angrenzen, wie sechs Räume an einen Flur. In dieser Variante muss sich jeder Akkordwechsel von einem Zimmer zum anderen durch den Flur bewegen, was zwar die Stimmführungsdistanz (als zwei ›Raumwechsel‹) korrekt wiedergibt, aber dafür alle Töne des übermäßigen Dreiklangs mehrfach darstellt.[9] Die eleganteste Darstellung ist der Weitzmann water bug,[10] ein Käfer bestehend aus einem Körper (übermäßig) und sechs Beinen links und rechts (Dur und Moll).

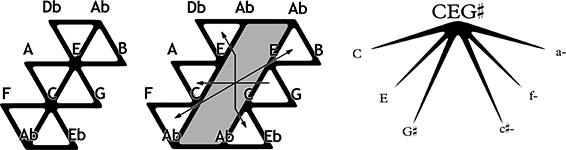
Abbildung 3: Darstellungen der Weitzmann-region links als Auschnitte des Tonnetzes, rechts als Weitzmann water bug

Die Visualisierung des hexatonic cycle (Abb. 4) ist nicht ganz so problematisch, gegen die Übernahme des ›Akkordbandes‹ aus dem Tonnetz spricht hier nur die Erscheinung der angrenzenden übermäßigen Dreiklänge als Achsenabschnitte.

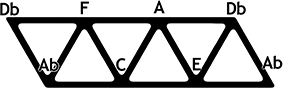
Abbildung 4: Der hexatonic cycle als Ausschnitt des Tonnetzes

Da den übermäßigen Dreiklängen in hexatonischen Verbindungen nicht dieselbe transitorische Rolle wie im Zusammenhang mit der Weitzmann-region zukommt, stellt dies aber auch kein direktes Problem dar und es wird erst im Zuge der Entwicklung des Cube Dance die Form des würfelförmigen Moduls gefunden, das bereits eine latente Dreidimensionalität aufweist (vgl. Abb. 2).

Ausgangspunkt meiner Weiterentwicklung ist nun die Annahme, dass der hexatonic cycle erst dann angemessen graphisch repräsentiert ist, wenn die übermäßigen Dreiklänge im Erscheinungsbild an die Dur- und Mollklänge angeglichen sind. So habe ich dreidimensionale Versionen des hexatonic cycle und der Weitzmann-region erstellt (Abb. 5), die darüber hinaus zusammen eine alternative Darstellung des Cube Dance ermöglichen.

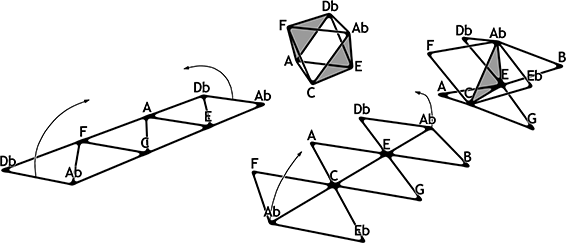
Abbildung 5: Dreidimensionale Modelle des hexatonic cycle und der Weitzmann-region

Diese Abbildung zeigt, wie man die entsprechenden Ausschnitte des Tonnetzes an ihren Enden ringförmig zusammenfügen kann. Dadurch erzeugen die dreigliedrigen Großterzachsen nach dem Zusammenschluss in ihrem Inneren ein neues Dreieck (im Bild grau), das den gesuchten übermäßigen Dreiklang repräsentiert. Im links gezeigten hexatonic cycle, der nun die Form eines liegenden Oktaeders hat, liegen alle Dreiecke mit P- und L-Verbindungen nebeneinander, der Austausch eines wechselnden Tones in einer solchen Verbindung kann als Rotation um die gemeinsame Achse wie im flachen Tonnetz vorgenommen werden. Es ist gut zu erkennen, dass jeder Dreiklang immer über jenen einen Ton ›im anderen Lager‹ verfügt, der chromatisch vom nächstverwandten übermäßigen Dreiklang abweicht. Die Partner einer H-relation liegen sich im Oktaeder ihrer Natur gemäß gegenüber. Die Weitzmann-region zur Rechten präsentiert sich als ›übermäßiges Dreieck‹ im Kern, umgeben von zwei fragmentarischen Tetraedern (die linke Hälfte taucht auch im abgebildeten cycle auf). Jede Akkordverbindung zwischen den am Rand gelegenen Dur- und Molldreiklängen in diesem Gebilde erfordert eine Rotation um eine Kante oder Ecke des Zentraldreiecks. Abbildung 6 zeigt, wie sich vier Weitzmann-regions so ineinanderstecken lassen, dass ihre gezackten Kanten sich zu vollständigen hexatonic cycles fügen. Im Komplex ergeben die miteinander verschränkten Module eine unendliche Hexentreppe (benannt nach dem Papiermodell, das Kinder aus zwei Papierstreifen falten), die alle Eigenschaften des Cube Dance besitzt.

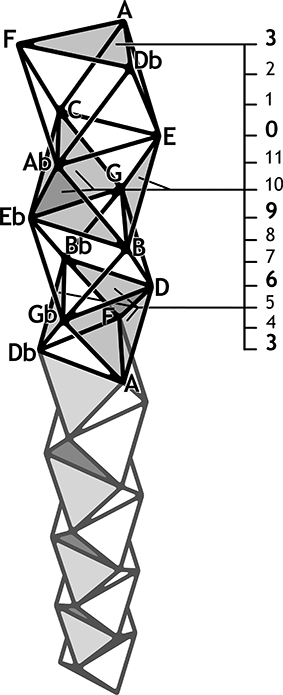
Abbildung 6: Hexentreppe

An der Spitze dieses Turmes liegt der hexatonic cycle aus Abbildung 5, unter ihm seine benachbarte Weitzmann-region. Den voice-leading zones entsprechen in diesem Turm vertikal geschichtete Ebenen: Alternierend je ein liegendes übermäßiges Dreieck (im Bild exemplarisch markiert zone 3), drei abwärts gerichtete ›Durdreiecke‹ (zone 5) oder drei aufwärts weisende ›Molldreiecke‹ (zone 10). Alle relations sind als reale Verbindungen von Dreiecken in dieser Darstellung enthalten – mit Ausnahme der H-relation, die wie oben schon besprochen aus zwei gegenüberliegenden Dreiecken besteht. Im Gegensatz zum Cube Dance stellt dieses Modell alle Akkorde als tatsächliche Tonkonstruktionen dar und macht damit auch alle gemeinsamen Töne ablesbar. Außerdem gleicht es die Dur-, Moll- und übermäßigen Dreiklänge in ihrer Gestalt an, womit vor allem letztere im Sinne Carl Friedrich Weitzmanns zu ihrem Recht kommen.[11] Allerdings erfüllt es nicht den Anspruch, keinen Ton doppelt wiederzugeben, da sich der Turm nach vier Segmenten um 120° gedreht wiederholt und prinzipiell unendlich fortsetzen lässt (wie in der Graphik angedeutet). Es ließen sich natürlich vier Segmente zu einer Art Torus[12] einrollen – das würde aber die gleichseitigen Dreiecke dehnen und verzerren und durch die erzwungene innere Torsion um 120° auch die Lesbarkeit einschränken. In der dargestellten Form bietet dieses Modell alle Vorteile des Cube Dance und stellt darüber hinaus alle Dreiklänge inklusive des übermäßigen als dem Tonnetz entsprechende Dreiecke dar. Es schöpft die dritte Dimension voll aus, ohne die der Cube Dance (in geringem Maße) auch nicht auskam.

Beispiel 1: J. S. Bach, Fantasie und Fuge g-Moll (BWV 542), T. 31–35

Der reale Quintfall aus Johann Sebastian Bachs Fantasie g-Moll für Orgel (BWV 542, Bsp. 1) schöpft seinerseits die Dimensionen der Hexentreppe voll aus: Er bildet auf ihr eine Spirale, die sich gegen den Uhrzeigersinn in den voice-leading zones nach oben schraubt (Abb. 7).

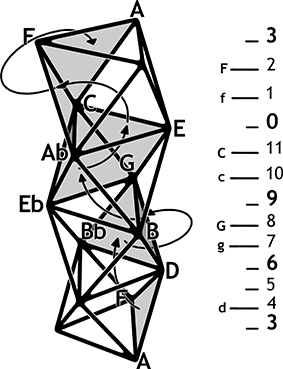
Abbildung 7: Realer Quintfall auf der Hexentreppe

Das Modell zeichnet jenes musikalische Moment nach, das gegenüber der katabasischen Pedalstimme und den sich stetig mehrenden -Vorzeichen fast ins Hintertreffen gerät, nämlich die Stimmführung der fünf nacheinander eintretenden Oberstimmen, deren imitiertes Motiv sich chromatisch aufwärts arbeitet. Als beständige Gegenkraft zu den anderen beiden abwärts wirkenden Momenten erzeugt sie die Spannung, die sich nach dem Absinken nach des-Moll (einer ›mörderischen‹ Tonart, zumal in einer wohltemperierten, wenn nicht mitteltönigen Stimmung) in mehreren verminderten Dreiklängen entlädt, die enharmonisch das angerichtete Unheil wieder entspannen. Diese verminderten Dreiklänge weisen auf die Struktur der Hexentreppe hin, die zwar (unhörbar) auf dem eingebauten übermäßigen Dreiklang basiert, andererseits jedoch über einen Stufenabstand von einer kleinen Terz (der Abstand der Weitzmann-regions voneinander: drei voice-leading zones) verfügt. Auch der Ambitus der imitierten Chromatik weist dieses Intervall auf und zeichnet somit einen Schritt auf der Treppe nach, von einer Weitzmann-region zur nächsten.

2. Die Vierklänge des Tristan-genus

Die Akkorde des Tristan-genus (unter dieser Familie subsumiert Cohn Dominantseptakkorde und halbverminderte Septakkorde) haben eine Reihe von Verbindungsmöglichkeiten, die 1998 von Adrian Childs[13] und Edward Gollin[14] ausgelotet wurden. Cohn gibt Childsʼ Bezifferungen an, die sich auf Akkordwechsel mit zwei chromatischen Stimmwechseln beziehen (Bsp. 2).

Beispiel 2: S- und C-relations

Die sechs S-Verbindungen beschreiben ähnlich wie die Slide-relation den parallel geführten Wechsel zweier Halbtonschritte – dass S in diesem Fall nicht für slide, sondern für similar motion steht, könnte man als kontrollierte Überschneidung zweier Bezeichnungssysteme beschreiben. Dabei kennzeichnet die hochgestellte Ziffer das gehaltene Intervall, im Fall von S³ ist in Klammern zur Unterscheidung noch das wechselnde Intervall mit angegeben. Die R^*-Verbindung ist ein Sonderfall, weil sich in ihr nur eine Stimme um zwei Halbtöne bewegt. Die anderen S-relations weisen jedoch konsequent zwei Wechsel- und zwei Haltetöne auf. Akkordfolgen aus S-relations könnte man mit Sätzen vergleichen, in denen aufeinanderfolgende Wörter zwei gleichbleibende Buchstaben enthalten. Wie die herkömmlichen Neo-Riemannian relations vollziehen auch die sieben oberen relations konsequent einen Wechsel des Geschlechts. Diese Eigenschaft fehlt Childsʼ drei C-relations (contrary motion, d. h. zwei Stimmen in Gegenbewegung), was auch Cohns Grund gewesen sein mag, sie nicht zu erwähnen. Diese drei relations vermitteln zwischen den identischen Akkorden auf den Stufen eines verminderten Septakkords. Dabei sind C³⁽²⁾ und C³⁽⁴⁾ inversibel, während C⁶ seiner eigenen Umkehrung entspricht. Die Vierklangs-relations lassen sich ebenso wie die Dreiklangs-relations in zwei Gruppen unterteilen, die später noch von Bedeutung sein werden: S³⁽²⁾, S³⁽⁴⁾, R^* und S⁶ bilden die Boretz-group transformations, die sich in den Grenzen der Boretz-region[15] bewegen (vergleichbar mit der Weitzmann-region). Gemeinsam mit einer Verbindung, die Cohn nach Childs den octatonic pole[16] nennt, ergeben S², S⁴ und S⁵ die octatonic-group transformations (O-group), die Progressionen innerhalb eines octatonic cycle[17] erzeugen. Graphisch darstellen lässt sich die Boretz-region, nach dem Prinzip des Weitzmann water bugs, als Spinne (Boretz spider) mit acht Beinen: Der Körper als verminderter Septakkord schart vier halbverminderte und vier Dominantseptakkorde um sich. Kombiniert mit den Octa Towers (graphische Darstellung des octatonic cycle als zweidimensional verflachter Rhombendodekaeder) von Jack Douthett und Peter Steinbach[18] ergibt sich das ebenfalls auf ihren Gedanken[19] aufbauende Modell des 4-Cube Trio (Abb. 8).

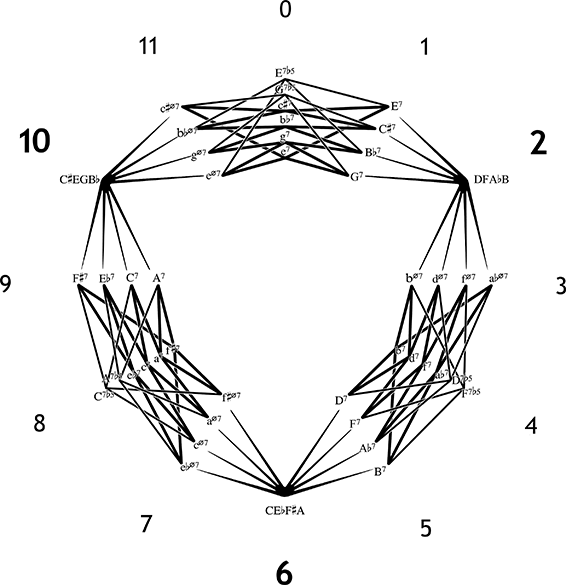
Abbildung 8: 4-Cube Trio

Dieses Modell unterteilt die Vierklänge nach dem Prinzip des Cube Dance in voice-leading zones und gruppiert sie gleichzeitig in Boretz-regions und octatonic cycles (einem Spinnennetz ähnliche Gebilde, mit sechs weiteren Akkorden in ihrer Mitte). Da die oben beschriebenen relations nur Operationen mit einer voice-leading distance von zwei working units gewähren (oder im Fall von C keiner working unit), müsste das Modell eigentlich nur ungeradzahlige Zonen enthalten. Douthett und Steinbach haben jedoch in ihrem Modell der Power Towers bereits vier kleine Mollseptakkorde ergänzt, die zwischen halbverminderten und Dominantseptakkorden vermitteln bzw. den virtuellen Zwischenschritt darstellen, der innerhalb einer Sⁿ- oder Cⁿ-Relation liegt. Cohn fügte noch den Dominantseptakkord mit tiefalterierter Quinte hinzu, der acht weitere Verbindungen innerhalb des octatonic cycles ermöglicht. Er taucht aufgrund seiner enharmonischen Doppeldeutigkeit nur sechsmal im ganzen Modell auf, erlaubt deswegen aber auch doppelt so viele Durchgänge von einer Seite eines cycle zur anderen. Diese addierten Vierklänge füllen die ansonsten leerstehenden Zonen 0, 4 und 8, sodass das komplette 4-Cube Trio alle durch einen Halbtonschritt benachbarten Akkorde über Achsen verbunden darstellt, alle Fortschreitungen mit mehr als einer working unit hingegen als getrennte, nur virtuell verbundene Akkorde. So muss man von E⁷ vier working units zurücklegen, bis man den octatonic pole g^Ø7 erreicht, der nur zwei voice-leading zones entfernt liegt – dafür stehen aber auch 18 Pfade zur Auswahl.

3. Das 3D-Tonnetz

Ein lästiger Umstand des 4-Cube-Trio und der ihm zugrunde liegenden Modelle, der die Vierklänge in der NRT bislang etwas ins Abseits gestellt hat, ist ihr hoher Grad an Abstraktion. Während den triadischen Überlegungen in jeder Hinsicht das Tonnetz als Grundlage dient, vermisst man bei den Vierklängen eine vergleichbare fassliche Basis. Allerdings verweist Cohn beiläufig auf den bereits erwähnten kurzen Artikel von Edward Gollin, in dem dieser die Struktur eines dreidimensionalen Tonnetzes vorstellt.[20] Es weist alle notwendigen Eigenschaften seines zweidimensionalen Bruders transferiert in den Raum auf (Abb. 9).

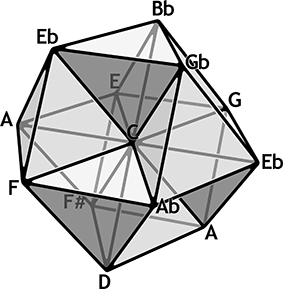
Abbildung 9: 3D-Tonnetz-Ausschnitt um C

Dieser Ausschnitt stellt die direkte Umgebung des Tones c dar, die aus acht Vierklängen besteht: Vier Dominantseptakkorde und vier halbverminderte Septakkorde. In der horizontalen Ebene kann man einen liegenden Ausschnitt des triadischen Tonnetzes erkennen, der sich ebenfalls um c erstreckt. Jeder Vierklang erscheint in der Form eines Tetraeders mit vier Tönen an den Spitzen, der aus dem c in der Mitte entspringt; vorne rechts sieht man beispielsweise As⁷, aufwärts weisend, in der Mitte oben c^Ø7, mit der Spitze abwärts gerichtet.[21] In diesem Ausschnitt sind alle möglichen relations von Akkorden des Tristan-genus enthalten, die über mindestens einen gemeinsamen Ton verfügen, d. h. alle Tetraeder haben entweder eine gemeinsame Achse – also zwei geteilte Töne – oder nur das c in der Mitte gemeinsam, drei gemeinsame Töne kommen in der Struktur dieses 3D-Tonnetzes nicht vor. Ausgenommen davon ist mit nur einem Ganztonwechsel die R^*-Relation, die im Netzausschnitt dreimal erscheint: As⁷/c^Ø7, D⁷/fis^Ø7 und F⁷/a^Ø7. Diese drei Verbindungen weisen syntonic images (identische Töne an verschiedenen räumlichen Positionen) auf, die an den Rändern des Ausschnitts zweimal vorkommen, wodurch die Partner jeweils drei gemeinsame Töne haben, statt, wie es auf den ersten Blick scheint, nur zwei. Die dritte Verbindung weicht in ihrer Struktur ab: Die ersten beiden Tetraederpaare sind über zwei Töne, die immer auf der Tritonus-Achse Fis-C-Ges liegen, verbunden – sie orientieren sich also an dieser Achse, die schon im begrenzten Umfeld um den Ton c die enharmonischen syntonic images Fis und Ges generiert. Das letzte Paar F⁷/a^Ø7 hat nur das zentrale c gemeinsam, dafür verfügt es über zwei syntonic images, die gemeinsamen Töne es und a, die auf zwei parallelen Tritonus-Achsen liegen. Eine zweite Anomalie findet sich bei genauerer Betrachtung der S⁶-relation: Die Verbindung As⁷/fis^Ø7 teilt ebenfalls nur den Ton c und liegt ebenso an der problematischen Tritonus-Achse (näheres zu dem Verhältnis dieser beiden relations folgt im kommenden Abschnitt). Vorerst möchte ich veranschaulichen, welchen Platz die Tritonus-Achse im Gefüge des 3D-Tonnetzes einnimmt (Abb. 10).

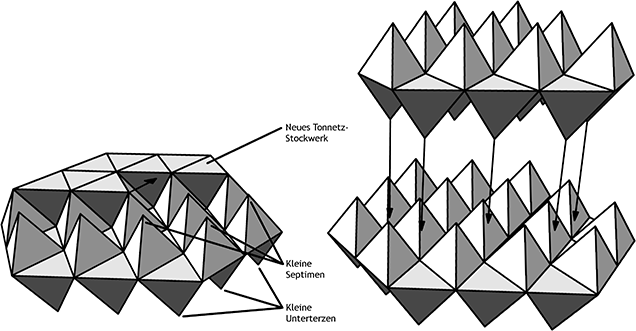
Abbildung 10: Konstruktion des 3D-Tonnetzes

Es gibt zwei Wege, auf Basis des Tonnetzes ein 3D-Tonnetz zu errichten. Der erste besteht darin, über jedem Dur-Dreieck eine Pyramidenspitze mit der kleinen Septime zu errichten (hellgrau/weiß) und unter jeden Molldreiklang eine kleine Unterterz (dunkelgrau) zu hängen,[22] sodass eine Art ›doppelseitiger Eierkarton‹ entsteht (Abb. 11). Es ist sowohl möglich, die Spitzen der Pyramiden zu verbinden und ein um eine kleine Septime transponiertes Tonnetz zu erzeugen, als auch von oben und unten Kopien des Eierkartons mit den Spitzen in die Täler des Originals zu senken; sie fügen sich nahtlos aneinander, aber es bleiben naturgemäß Hohlräume in Oktaederform. Auf beide Arten werden neue Tonnetz-Stockwerke erzeugt, von denen aus enharmonisch unendlich weitergebaut werden kann.

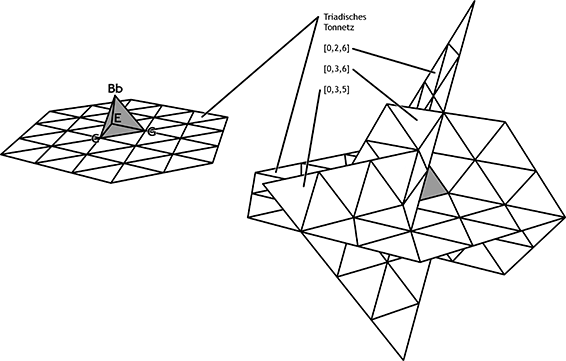
Abbildung 11: Verschränkte Tonnetze um einen Tetraeder

Der zweite Weg ist umständlicher und widerstrebt dem bequemen Denken in Schichten, kann aber die Struktur des 3D-Tonnetzes tiefer gehend veranschaulichen: Ein Tetraeder (z. B. C⁷, vgl. Abb. 11 links) ist umgeben von seinen vier Tönen und umfangen von den sechs Intervallachsen, die alle in ihm enthaltenen Intervalle darstellen [2,3,3,4,5,6].[23] Außerdem ist er ummantelt von vier Flächen, die jene vier Dreiklänge darstellen, die in ihm enthalten sind (CEG, CEB, CGB, EGB). Der Dreiklang CEG ist die Ausgangsfläche des (liegenden) triadischen Tonnetzes. Es lassen sich aber ebenso an den drei anderen Flächen diagonal im Raum stehende Tonnetze erzeugen (Abb. 11 rechts), denen andere sets zugrunde liegen: [0,2,6], [0,3,5], [0,3,6].[24] Die vier den Tetraeder umgebenden Netze sind ineinander verschränkt und lassen sich im Raum weiter fortsetzen, sodass sie das 3D-Tonnetz mitsamt Vierklängen erzeugen. Das 3D-Tonnetz ist also nicht nur eine Übersteigerung des zweidimensionalen Prinzips, es ist ein räumliches Produkt aus zweidimensionalen Tonnetzen.

Aus der (willkürlichen bzw. allenfalls aus dem Obertonspektrum abgeleiteten) Wahl des Dominantseptakkordes [0,4,7,10] als Basis des 3D-Tonnetzes folgt einerseits, dass eines der vier enthaltenen 2D-Tonnetze nicht wie gewohnt das chromatische Total abdeckt, sondern nur über die vier Töne des verminderten Septakkordes verfügt; dieses ›sterile‹ Netz [0,3,6] besteht nur aus verminderten Dreiklängen, die umkehrungsgleich sind und beinhaltet darüber hinaus eine Tritonus-Achse, die bereits nach zwei Schritten wieder ein syntonic image repetiert. Andererseits schränkt die Wahl des Tristan-genus die direkte Umgebung ein, die nicht die kleine Sekunde und die große Septime enthält – jene zwei Intervalle, die in [0,4,7,10] nicht vorkommen. In den zwölf Tönen, die das c in Abbildung 9 umgeben, sind folglich die drei Töne ges, es und a doppelt vorhanden, da sie alle auf dem verminderten Netz um c liegen. Die ausgesuchten R^*-Verbindungen F⁷/a^Ø7, D⁷/ges^Ø7 und As⁷/c^Ø7 liegen alle an dieser problematischen Ebene und ergeben trotz räumlich verschiedener Struktur den gleichen Akkordwechsel.

Gollin hat das 3D-Tonnetz als mathematisches Gerüst vorgestellt, in das neben dem Tristan-genus jedes beliebige set aus vier Tönen gemeinsam mit seinem dualistischen Partner[25] eingefügt werden kann. Vier weitere Möglichkeiten fallen ins Auge:

Erstens die beiden Allintervallklänge, hier exemplarisch [0,1,3,7]: Seine namensgebende Form bildet eine Umgebung aus, in der nur der Tritonus doppelt vorkommt.[26] In dieser kaum von syntonic images getrübten, friedvollen Umgebung gedeihen sechs S-relations, von denen sich nur eine, nämlich S³, in zwei parallelen Halbtonschritten fortbewegt – S¹, S², S⁴ und S⁵ haben eine similar motion in Kleinterz-, und S⁶ sogar in Quartschritten.

Zweitens der hartverminderte Septakkord oder übermäßige Terzquartakkord [0,4,6,10]. Da er umkehrungsgleich und außerdem ein Ausschnitt der Ganztonleiter ist, erzeugt er ein sechstöniges 3D-Tonnetz, das an ›Sterilität‹ nur noch durch das verminderte Netz [0,3,6,9] überboten wird.

Drittens und viertens der kleine Mollseptakkord [0,3,7,10] und der große Durseptakkord [0,4,7,11] (Bsp. 3). Sie sind ebenfalls umkehrungsgleich und erzeugen um einen Ton somit eine direkte Umgebung, in der nur vier Akkordtranspositionen je zweimal auftauchen.

Beispiel 3: Verbindungen von kleinen Moll- und großen Durseptakkorden

Dieses Netz stellt zuverlässig alle intern möglichen Verbindungen mit zwei oder drei wechselnden Tönen dar, erzeugt jedoch auch zwei ›Homophone‹,[27] die trotz räumlicher Veränderung keinen einzigen Ton des Ausgangsakkords ändern.

4. Heart Cubes

Es ist nicht zu leugnen, dass das 3D-Tonnetz beträchtliche räumliche Vorstellungskraft erfordert, insbesondere wenn der Maßstab über die Grenzen der direkten Umgebung eines Tons hinauswächst. Ich schlage darum ein transformiertes Netz vor, in dem die Tetraeder zu Punkten zusammengezogen und ihre S-Verbindungen als Achsen dargestellt sind (Abb. 12); das Resultat trägt in Anlehnung an die fantasievoll betitelten amerikanischen Modelle den Namen Heart Cubes.

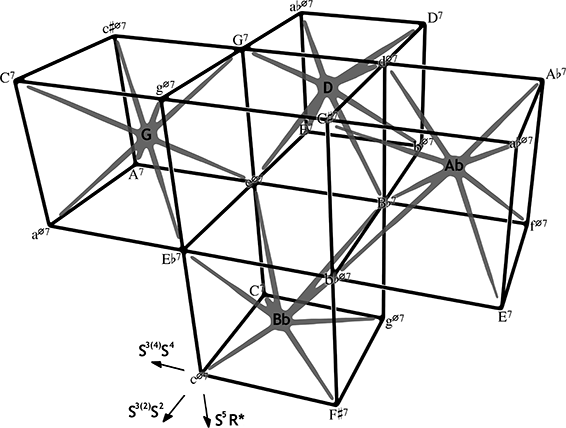
Abbildung 12: Heart Cubes

Der Ausschnitt zeigt vier Töne mit ihrer jeweiligen direkten Umgebung. Jede hat die Form eines Würfels, der in seiner Mitte als Heart jenen Ton trägt, den die acht Akkorde an den Ecken gemeinsam beinhalten. Fortlaufend aneinander gereiht bilden die Heart Cubes mit ›herzlosen‹ Würfeln[28] alternierend ein dreidimensionales Schachbrettmuster aus. Von jedem Septakkord streben auf den sechs Achsen sechs verschiedene S-relations fort (jede Achse besteht aus zwei sich abwechselnden relations, je eine aus der Boretz- und eine aus der O-group), allerdings fehlt S⁶, abgebildet ist hingegen R^*. Die Diagonalen auf den quadratischen Würfelflächen lassen sich durch zwölf verschiedene Kombinationen aus je zwei S-relations (oder R^*, aber nicht S⁶) ausdrücken, die verbleibenden drei Kombinationen laufen in einer Richtung alternierend auf einer Achse. Es fehlen der octatonic pole und S⁶; ersterer liegt auf zwei Raumdiagonalen im herzlosen Würfel, letztere auf die gleiche Weise diagonal in den Heart Cubes, z. B. die Verbindung A⁷/g^Ø7 im G-Würfel.[29] In ihr wird der kritische Ton cis enharmonisch zu des umgedeutet, was dafür sorgt, dass die S⁶-relation nicht wie alle anderen S-/R^*-relations auf einer der Würfelkanten liegt, sondern (mit zwei klingend aber drei enharmonisch/räumlich verschiedenen Tönen) durch eine größere räumliche Distanz dargestellt ist. S⁶ allein erzwingt eine enharmonische Umdeutung, die bei allen anderen relations nicht notwendig ist. Aus diesem Grund liegt S⁶ nicht auf einer der Achsen; das Modell der Heart Cubes kann besser als das 3D-Tonnetz diese Anomalie von S⁶ und R^* veranschaulichen.

Obwohl lediglich in viel entfernteren relations – Korrelationen ohne relativ tonartgebundenes Erscheinungsbild – verknüpft, lassen die vier internen Dominantseptakkorde A⁷, C⁷, Es⁷ und G⁷ um den Ton g den erheblichen Einfluss der dualistischen Lehre spüren. Ihre Grundtöne ruhen auf vier Tönen, die einen halbvermindertem Septakkord ergeben. Umgekehrt ergeben a^Ø7, e^Ø7, cis^Ø7 und g^Ø7 einen flach liegenden Dominantseptakkord. Die beiden Partner zitieren sich gegenseitig als Akrostichon[30] – diese hübsche Eigenart rührt her vom Zusammenhang der vier möglichen Transpositionen eines Vierklangs um den Ton g, die den verwendeten Akkord zwingen, sein eigenes Spiegelbild als Fußstapfen zu hinterlassen, und ist ein gutes Exempel dafür, dass schon Weitzmanns dualistische Äußerungen, die auf Hauptmann Bezug nahmen, nicht ohne Grund waren und auf innere Strukturen hinwiesen, die essentiell für unser Tonsystem sind.

In den Heart Cubes tauchen auch Childsʼ C-relations innerhalb der Flächendiagonalen auf, und bestätigen damit scheinbar Cohns Entscheidung, sie nicht zu erwähnen: Sie lassen sich als Kombination darstellen, z. B. C³⁽⁴⁾=S²S⁵. Allerdings ist diese Kombination widersinnig, da die beiden S-relations zusammen eine viel größere virtuelle Stimmführungsarbeit erzeugen als sich in C³⁽⁴⁾ tatsächlich vollzieht.[31] Die drei C-relations sind insofern von Bedeutung, als sie jene drei Modulationen darstellen, die die drei Boretz-group transformations (S³⁽²⁾, S³⁽⁴⁾ und S⁶) und die drei O-group transformations (S², S⁴ und S⁵) intern miteinander kombiniert ergeben. Die C-relations bewegen sich also ausschließlich in den Grenzen einer Boretz-region bzw. eines octatonic cycle.[32]

5. Die Vierklangs-Spindel

Die Heart Cubes liefern nicht mit allen sets befriedigende Ergebnisse; statt aus Dominantseptakkorden aus kleinen Mollseptakkorden konstruiert, stellt das gleiche Gitter zwar in der Horizontalen den Vorrat an möglichen relations dar, diese Ebene wiederholt sich jedoch exakt kopiert in der Vertikalen: Die oben genannten ›Homophone‹ sorgen dafür, dass die senkrechten Achsen jeweils nur einen einzigen duplizierten Akkord wiederholen. Nichtsdestotrotz haben auch der kleine Mollseptakkord, der große Durseptakkord, der hart verminderte Septakkord und einige mehr ihren festen Platz in der Musik, und es ist bedauerlich, dass sowohl das 3D-Tonnetz als auch die Heart Cubes nicht mit ausreichenden Fähigkeiten ausgestattet sind, alle diese Klänge in Verbindung miteinander zu bringen. Cohn hat den Versuch gemacht, das 4-Cube Trio um zwei dieser Akkorde zu erweitern; ich möchte hier meine Weiterentwicklung, die Vierklangs-Spindel, vorstellen (Abb. 13). In ihr ist das ganze System auch noch um andere Vierklänge, z. B. den großen Durseptakkord, ergänzt.

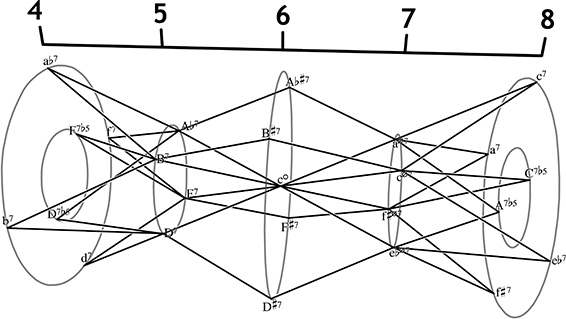
Abbildung 13: Die Vierklangs-Spindel

Dieser Ausschnitt aus der Vierklangs-Spindel bildet ein Drittel der zwölf voice-leading zones ab. Gruppiert um den verminderten Septakkord c° stellt sie fünf Klassen von terzgeschichteten Vierklängen ins Verhältnis. Durch Achsen verbundene Akkorde weichen stets um einen Halbtonschritt voneinander ab, die S-relations sind also indirekt als Kombinationen aus zwei Schritten zwischen den ungeradzahligen Zonen wiedergegeben. Zwischen den Zonen 5 und 7 erstrecken sich die Boretz-group transformations – die R^*-relation hat einen vollwertigen Platz unter ihren Gruppenmitgliedern. In der nicht vollständig in der Abbildung enthaltenen O-group, zwischen den Zonen 3 und 5, liegt der octatonic pole als diagonale Verbindung, die nur über verschiedene Pfade aus vier Halbtonschritten hergestellt werden kann. R^* und der octatonic pole ergänzen so die jeweils drei S-relations einer group. Das Spindelmodell stellt also verwandte relations, die im 3D-Tonnetz aufgrund der spezifischen Gestalt der Tristan-genus-Vierklänge divergieren, gleichberechtigt nebeneinander.

Darüber hinaus eröffnet es die Möglichkeit, auch Verbindungen von halbverminderten zu dominantischen Septakkorden über große Durseptakkorde darzustellen, die einen Weg alternativ zum Gang durch den verminderten Septakkord bilden (Abb. 14).[33] Konkret heißt das: Lässt man die beiden Halbtonschritte einer relation aus der Boretz-group sukzessive eintreten, entsteht als Durchgangsakkord entweder ein verminderter oder ein großer Dur-Septakkord. Zwischen den asymmetrischen (über zwei Zonen benachbarten) Akkorden des Tristan-genus kann im Spindelmodell prinzipiell auf zwei Wegen vermittelt werden: Über symmetrische Akkorde mit mehr als zwei Spiegelachsen (verminderter/hartverminderter Septakkord) oder über spiegelbildliche Akkorde (großer Dur-/kleiner Mollseptakkord). Die voice-leading zones klassifizieren die Akkorde in asymmetrische Klänge in den ungeraden Zonen und (verschiedenartig) symmetrische Klänge in den geradzahligen Zonen. Übereinstimmend mit dieser Klassifizierung wäre es möglich, in die ungeraden Zonen weitere Vierklänge einzufügen, welche nur die äußeren Ringe verbinden würden. In der asymmetrischen Zone 5 wären das große Mollseptakkorde [0,3,7,11] über as, h, d und f und in Zone 7 über denselben Tönen große übermäßige Septakkorde [0,4,8,11] als dualistische Gegenparts. Diese Klänge würden auf großen Ringen die kleinen Tristan-genus-Ringe umschließen und hätten nur Verbindungen zu den großen Ringen der benachbarten Zonen. In den geraden Zonen 2, 6 und 10 wäre es weiterhin möglich, den sogenannten ›Chopin-Akkord‹ mit kleiner Sexte [0,2,4,8] als Alternative zu dem Ring der großen Durseptakkorde einzufügen; er würde Vierklänge der oben beschriebenen S⁶-Relation verbinden, z. B. D⁷/c^Ø7. In den geraden Zonen lassen sich als Vermittler der vorigen Ebene schließlich der ›Bartók-Akkord‹[34] [0,3,4,7] (B, in den voice-leading zones 2, 6 und 10) und der übermäßige Dreiklang [0,4,8,12] (Ü, voice-leading zones 0, 4 und 8) – als virtueller Vierklang mit übermäßiger Septime – einführen. Von diesen Klängen ausgehend müssten bereits vier Halbtonschritte aufgewendet werden, um zum verminderten Septakkord im Zentrum zu modulieren. Alle hinzugefügten Klänge stehen genetisch in enger Verbindung zum zweidimensionalen Tonnetz. Der kleine Moll- und der große Durseptakkord entspringen aus der Addition der Partner einer R- bzw. einer L-relation, der ›Bartók-Akkord‹ aus einer summierten P-relation. Der Tristan-genus besteht aus einem Dur- oder Moll- plus vermindertem Dreiklang, der große übermäßige und der große Mollseptakkord enthalten dafür den übermäßigen Dreiklang – der auch eigenständig schon eingeführt wurde.

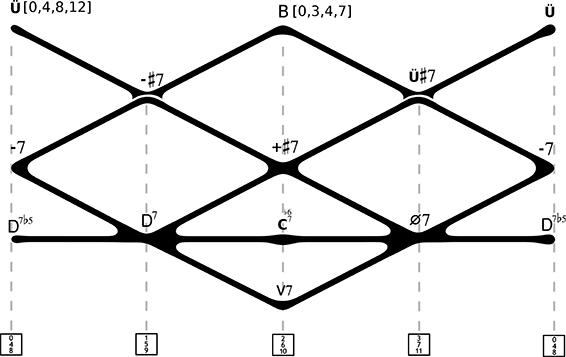
Abbildung 14: Verallgemeinerter Spindelquerschnitt

Dieser schematische Spindelquerschnitt ist flach um die Mittelachse herum zusammengefaltet, um die Verbindung zwischen den Vierklangsklassen im Allgemeinen abzubilden. Dabei sind auch diagonale Verbindungen übereinandergelegt, die zu gleichen Akkordklassen, nicht aber zu tatsächlich identischen Klängen führen. (Ein konkreter Dominantseptakkord kann nicht über drei Wege mit einem anderen konkreten halbverminderten Septakkord zwei Zonen höher verbunden werden, wie die drei Pfade im Kern missverständlicherweise nahelegen, sondern nur über drei Wege mit drei unbestimmten Akkorden dieser Gattung!) In den oberen Sphären schweben ›entrückt‹ der Bartók-Akkord und der übermäßige Dreiklang, der mit dem verminderten Septakkord die Ränder eines Feldes der chromatischen Stimmführung bildet. Natürlich ließe sich dieses vereinfachte Schema wieder in eine dreidimensionale Spindel auseinanderfalten, zu viele dargestellte Akkordklassen lassen das Modell aber unhandlich werden; in der praktischen Analyse bietet es sich an, nur die jeweils benötigten Ringe zu verwenden. Der Chopin-Akkord mit großer Sexte fehlt nicht ohne Grund: Er lässt sich nur über mindestens zwei Halbtonschritte mit den anderen kategorisierten Vierklängen (außer dem kleinen Chopin-Akkord) verbinden. Das hängt unter anderem mit seinem set [0,1,3,7] zusammen: Er ist ein Allintervall-Akkord, dem das weiter oben beschriebene Tonnetz mit besonders vielfältigen S-relations zugrunde liegt.

Beispiel 4: Hugo Wolf, Einklang (Sechs Geistliche Lieder), T. 9–16

Ein Beispiel für diese unterschiedliche Kompatibilität der beiden Chopin-Akkorde ist der Chorsatz »Einklang« aus Hugo Wolfs Zyklus Sechs geistliche Lieder (1881) nach Gedichten von Joseph von Eichendorff (Bsp. 4). Im Mittelteil (T. 9–16) thematisiert Wolf den Chopin-Akkord, der dreimal als Durchgang in verschiedenen Umkehrungen auftaucht. In Takt 10 wird er als großer Chopin-Akkord auf d eingeleitet von zwei typischen S-relations (aus der O-group), die eine Transposition um eine kleine Terz aufwärts (also innerhalb des octatonic cycle) bewirken, und eingerahmt von zwei atypischen Verbindungen, die im Sinne Childsʼ als C-relations verstanden werden können, da sie beide aus zwei entgegengesetzten Halbtonschritten bestehen – die Bezifferung gibt das gehaltene Intervall und in Klammern die wechselnden Intervalle an. Das gleiche set des großen Chopin-Akkords [0,1,3,7] wird in der dualistischen Umkehrung [0,4,6,7] in Takt 15 noch einmal gestreift,[35] diesmal vom Dreiklang G-Dur ausgehend, der sich im Gegensatz zu den Vierklängen mit nur einem Halbtonschritt anbinden lässt. Es handelt sich kaum um einen Zufall, dass Wolf diese beiden Akkorde im subdominantischen B-Teil effektvoll und leuchtkräftig auf der ersten und vierten Stufe positioniert hat. Als Bekräftigung dient der Halbschluss in den Takten 15 bis 16, in denen Wolf die bessere chromatische Anbindungsfähigkeit des kleinen Chopin-Akkords exerziert (er erscheint nicht in der gewohnten Schichtung). In den Kästchen in Beispiel 4 sind die jeweiligen voice-leading zones der Akkorde angegeben; solch dichte Progressionen lassen sich gut in einer Spindel wiedergeben (Abb. 15).

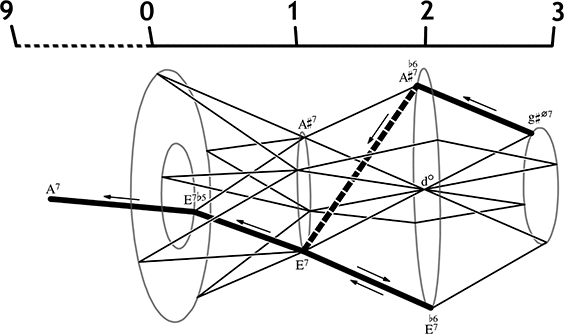
Abbildung 15: Chromatischer Halbschluss in der Spindel

In diesem Fall wurde der Ring mit großen Durseptakkorden durch den benötigten Ring mit kleinen Chopin-Akkorden ersetzt – alle nicht benötigten Akkordringe sind ausgeblendet. Bis auf den schließenden Quintfall (voice-leading zone 12 nach 9) liegen alle Akkorde in benachbarten Zonen. Nur der Wechsel Ais⁷⁶/E⁷ läuft diagonal durch die Spindel;[36] abgesehen von ihm – und einem kurzen a-Moll-Quartsextakkord, der aber eher als Durchgangsresultat eines angetäuschten Stimmtauschs zwischen Bass und Tenor zu betrachten ist – beinhaltet die Kadenz ausschließlich Vierklänge, die über einen einzigen Halbtonschritt verbunden sind. Nachdem der B-Teil endlich auf der Subdominante angekommen ist, führt diese Passage mit ihrem Kreisen in einem doppeldominantischen Feld zur Dominante A-Dur und damit in die variierte Reprise des A-Teils zurück.

Ein kleines Klavierstück von Alexander Skrjabin bietet Raum für Demonstrationen fast aller beschriebenen Phänomene: Das Allegretto in a-Moll aus den 24 Préludes op. 11 (Bsp. 5).

Beispiel 5: Alexander Skrjabin, Allegretto op. 11/2, Takte 47–68

In der unterlegten Analyse des Stücks werden die linearen Melodietöne zu Harmonien zusammengefasst, die nicht ausschließlich vertikal, sondern auch in Form von horizontalen Akkordbrechungen oder virtueller Polyphonie erscheinen. In Takt 47 und 48 direkt vor der Reprise schreitet B⁷ über drei chromatische Schritte nach f^Ø7 – diese Harmonie (mit gis, h und dis statt as, ces und es) würde herkömmlicherweise nicht eigenständig betrachtet, sondern als chromatische Umspielung des Zieltons abgetan, die verspätet über S³⁽²⁾ in die angesteuerte Dominante E⁷ mündete, welche von den Unterstimmen bereits am Taktbeginn etabliert wurde, ebenfalls über drei chromatische Schritte von B⁷ ausgehend. In den bezifferten Kästchen sind die relativen Schritte in den voice-leading zones angezeigt, um alle Fortschreitungen zu klassifizieren, die nicht Childsʼ relations entsprechen. Akkordwechsel mit drei chromatisch geführten Stimmen kommen im ganzen Stück gehäuft vor – sie lassen sich, wie bereits im Stück von Hugo Wolf gezeigt, als Kombination in der Spindel deuten. In den meisten Fällen summieren sie sich zu einem einzelnen Schritt abwärts, nur zweimal ergeben sie einen Sprung um drei voice-leading zones nach unten[37] wie beim Taktwechsel 56–57,[38] wo sie zweifach in der Modulation zum zweiten Teil des A-Themas auftreten. Innerhalb von drei Akkorden wird hier das 4-Cube Trio zur Hälfte umrundet. Anschließend wird vom erreichten G⁷ über zwei C³⁽²⁾-relations um zwei Kleinterzen abwärts moduliert, was wiederum in der herkömmlichen Musiktheorie einer halben Umrundung des Quintenzirkels entspräche, in unseren Modellen aber nur dem Verweilen in einer Zone. Bemerkenswert ist schließlich noch die Coda: Die Töne über dem einmaligen Bassthema in Takt 65 lassen sich zwar nur spekulativ den Akkorden G⁷, E⁷ und d-Moll zuordnen und fallen damit aus dem Rahmen, im vorletzten Takt wird dann jedoch das Prinzip des Orgelpunkts kraftvoll übersteigert, indem die drei relations R*, S⁵ und S⁶ schrittweise den Vierklang von oben herab auf die Dominante E⁷ herunterziehen. Alle drei kommen zum ersten Mal vor.

Abgesehen von diesen herausstechenden Stellen findet man zuhauf Sⁿ-relations, Halbtonschrittwechsel (gekennzeichnet mit -1) und mehrfach unbestimmte C-relations, die (z. B. in Takt 49) mittels zweier Stimmschritte in einer Zone verbleiben, aber die Akkordklasse ändern. Teilweise ist der Satz durchwirkt mit herkömmlichen diatonischen Verbindungen, beinahe dem gesamten Stück liegen jedoch zwei Prinzipien zugrunde: Bis auf eine Ausnahme (Takt 9, cresc.) haben alle aufeinanderfolgenden Akkorde mindestens einen Ton gemeinsam und im Großteil der Fälle überwiegt die Chromatik abwärts deutlich.

6. Multiples 3D-Tonnetz

Ungeachtet der möglichen Erweiterungen können aus dem ›Spindelmodell‹ – selbst in der dargestellten reduzierten Fassung – wie gerade gezeigt Verbindungen gesponnen werden, die die Kompetenzen des 3D-Tonnetzes sprengen. Fast alle Varianten von 3D-Netzen kranken an Unregelmäßigkeiten durch syntonic images, die je nach Struktur des Ausgangsakkords verschieden häufig auftreten und die relations aus dem Gleichgewicht bringen. Außerdem besteht zwischen dem Tristan-genus-Netz und den Netzen anderer Vierklänge kein Konnex. Als Folge davon kann die Verbindung von zwei Vierklängen, zwischen denen die Differenz einer einzigen working unit besteht, nicht so dargestellt werden, dass alle gleichen Töne auch räumlich identisch sind und sich ein einzelner Tonwechsel wie im Tonnetz als ›umklappende Ecke‹ vollzieht. Ich möchte eine Erweiterung des 3D-Tonnetzes vorschlagen, die es möglich macht, die verschiedenen Akkordklassen miteinander zu verbinden, ein multiples mehrdimensionales Tonnetz (Abb. 16).

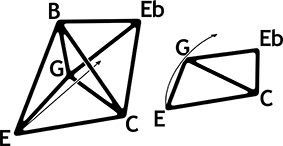
Abbildung 16: C⁷/c⁷ und P-relation

In dieser Abbildung wird ein klarer Bruch mit den geometrischen Gesetzen des 3D-Tonnetzes herbeigeführt, um den Wechsel C⁷/c⁷ an die Darstellung der einfachen P-relation C-Dur/c-Moll anzugleichen. Gebrochen wurde die flache Ebene, indem das hintere Es und damit der fiktive, dahinter liegende Netzbereich an der Achse G-C nach oben gekippt wurde. Gebrochen wurde auch das Tristan-genus, das nach vollzogenem Tonschritt sozusagen durch ein ›Wurmloch‹ verlassen wurde – an seiner Statt befindet man sich in einem ›Paralleluniversum‹, dem 3D-Tonnetz der kleinen Mollseptakkorde. Dadurch, dass im gewöhnlichen 3D-Tonnetz die Fläche C-G-B des C⁷-Akkords an einen leeren Oktaeder-Hohlraum grenzt und eine Fortbewegung bisher nur über die Tetraederachsen und -spitzen möglich schien, muss diese Progression aus Sicht des C⁷-Klangs tatsächlich wie ein Sprung durch ein Wurmloch anmuten. Nach dem Sprung baut sich um den neuen Akkord c⁷ eine neue Umgebung der Möglichkeiten auf. Klassische Fortschreitungen entlang der Achsen und Spitzen, aber auch ungewohnte neue Optionen, durch jede der vier Ebenen in wiederum andere Dimensionen, sind vorstellbar. Beispielsweise durch die Es-G-B-Ebene hindurch nach Es⁷ oder durch den c-Moll-Dreiklang hinunter nach a^Ø7. Aber man kann sich auch aus der dritten wieder in die zweite Dimension hinunterbegeben und die Bewegung im Umfeld um den c-Moll-Dreiklang auf dem gekippten Tonnetz fortsetzen – in diesem Fall würden die beiden Vierklänge zu einem Scharnierelement, welches zwei entfernte Tonnetze verbände. Der Grundgedanke, um diese Modulationen darstellen zu können, ist die Auflösung des festen Umfelds eines Drei- oder Vierklangs. Befreit man einen Akkord von dem starren, ihn umgebenden Netz und umgibt ihn dafür mit allen hypothetischen Bewegungen, die geometrisch vorstellbar sind, kann er sich frei in jede beliebige klangliche Dimension entwickeln!

Beispiel 6: Hugo Wolf, Wunden trägst du, mein Geliebter (Spanisches Liederbuch), T. 1–4

Diese Einleitung eines der geistlichen Lieder aus dem Spanischen Liederbuch von Hugo Wolf (»Wunden trägst du, mein Geliebter« – Text von Emanuel Geibel, Bsp. 6) lässt sich gut mit den beschriebenen Mitteln darstellen (Abb. 17).[39]

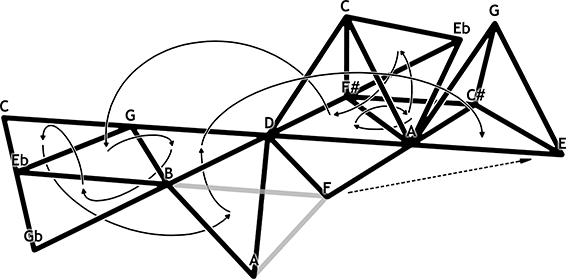
Abbildung 17: Progression in einem multiplen 3D-Tonnetz um d-Moll

Die harmonische Progression umkreist einige Takte lang die Tonika d-Moll, die erst zum Schluss der Phrase in Takt 6 erreicht wird. In Takt 2.3 wird die Dimension des Tristan-genus erstmalig verlassen und das Geschehen taucht kurzzeitig in die Welt der verminderten Septakkorde ein. Über die Fläche fis-a-c kehrt die Bewegung über D⁷ zurück auf das flache Tonnetz und springt in einen subdominantischen Bereich links von d-Moll. In Takt 4.2 wird ein zweites Mal eine fremde Dimension gestreift: der nach unten hängende – und damit dem um eine working unit entfernten B⁷ gespiegelt entgegenstehende – B⁷, der ohne das f als unvollständiger Akkord erklingt (theoretisch wäre auch ein übermäßiger Septakkord mit fis denkbar). Nach dem erneuten Schwenk über die Subdominante macht die Entwicklung einen jähen Satz über die Tonika hinweg zur Dominante A⁷, die melodisch in Form eines kleinen Chopin-Akkords die bisher unterschlagene Mollterz f der Tonika emanzipiert. Natürlich ließe sich auch dieser Akkord als fremder Tetraeder einbauen, er würde jedoch an der Fläche A-Cis-G angesetzt und damit in den verminderten Septakkord über fis hineinragen[40] – ein Zeichen dafür, dass bei Wolf vor allem im dominantischen Bereich eine verhältnismäßig große chromatische Erweiterung stattfindet! Diese Art der Visualisierung vermag auf einfachem Wege Areale wie den dominantischen und den subdominantischen Bereich darzustellen und Erweiterungen des Ton- und Akkordmaterials passend mit dem grundlegenden Tonnetz zu verknüpfen!

Bei stetig modulierenden Stücken stößt auch diese Darstellung an ihre Grenzen, weil sich der Verlauf eines Stückes meist als im Raum wucherndes Gebilde herausstellt, das an den Bau eines verknoteten Proteins erinnert. Der oben diskutierte Ausschnitt aus Skrjabins Prélude hat sich als nur schwer visualisierbar herausgestellt, da erstens Passagen wie die Takte 49 bis 52, in denen mehrere Akkorde aus einer Umgebung gleicher Töne (d und f) vorkommen, im Raum zu dichten Ballungszentren mutieren und zweitens die ununterbrochene Kette mit wachsender Länge ihren eigenen Pfad im Raum schneidet. Allerdings kann man eine solche Struktur in Teilglieder zerlegen, innerhalb derer sich dann die verschiedenen Unterstrukturen sehr gut visualisieren und unterscheiden lassen (Abb. 18). Die Takte 52 bis 53 bilden z. B. eine kleine Quintachse aus, die die feste Bindung der entsprechenden Akkorde A⁷, d-Moll und g⁷ unterstreicht. Die Sⁿ-Folgen, z. B. in den Takten 51 bis 52, ergeben einen engen Verbund von Tetraedern, die kontinuierlich an einer Achse zusammenhängen.

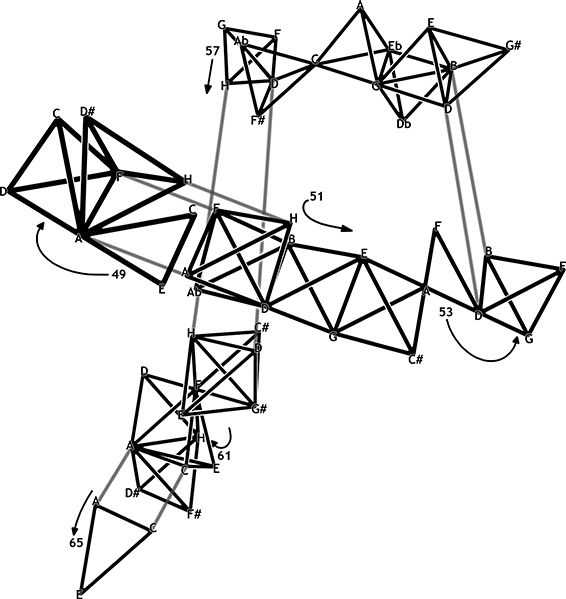
Abbildung 18: Skrjabins Prélude op. 11/2 im multiplen 3D-Tonnetz

Diese Art der Visualisierung verdeutlicht als Schlusspunkt meiner Überlegungen, dass das Modell eines multiplen 3D-Tonnetzes vor allem im kleinen Maßstab anwendbar ist und über größere harmonische Strecken allzu komplexe Resultate liefert.

Generell liegen die Stärken meiner vorgestellten Modelle – der Hexentreppe, der Heart Cubes, der Vierklangs-Spindel und des multiplen 3D-Tonnetzes – nicht im großen Maßstab, sondern im eng gefassten Analysebereich. Sie beschäftigen sich im Sinne der NRT mit symmetrischen Strukturen, um besondere musikalische Sachverhalte darstellen zu können, die aus den gewohnten Rastern fallen und schaffen im Kleinen einen neuen Blick auf verborgene Zusammenhänge.