Was ist ein musikalisches Modell?

In der Ausgabe 4/1–2 der Zeitschrift der Gesellschaft für Musiktheorie finden sich in den Beiträgen von Oliver Schwab-Felisch[1] und Hans-Ulrich Fuß[2] in Verbindung mit Satzmodellen die Worte ›abstrakt‹ und ›Instanz‹ bzw. ›Instantiierung‹ (im Folgenden ›Instanzierung‹). Beide Worte werden in der Objektorientierten Programmierung (OOP) als Fachbegriffe gebraucht, mit ihnen verbindet sich heute ein spezifisches Denken bzw. umfassendes theoretisches Konzept. Obgleich dieses bereits in anderen Wissenschaftsgebieten erfolgreich adaptiert wird, sind Bemühungen, zumindest Teile des Konzepts auch für die musikalische Analyse fruchtbar zu machen, noch nicht üblich. Aus diesem Grunde wird hier der Versuch unternommen, das Denken in Klassen und Instanzen anhand des Themas ›musikalische Modelle‹ zu erläutern und mögliche Bedeutungen des Ansatzes für den wissenschaftlichen Diskurs des Fachs Musiktheorie aufzuzeigen.[3]

Der Begriff ›Klasse‹ ist in der Objektorientierung ein abstrakter Oberbegriff, der die gemeinsame Struktur und das gemeinsame Verhalten von Objekten beschreibt. Klassen sind Abstraktionen von Objekten, Objekte wiederum repräsentieren Instanzen[4] (Exemplare) ihrer zugehörigen Klasse.[5] Verschiedene Klassen ermöglichen die Modellierung eines abgegrenzten Systems. Wenn unter ›Klasse‹ im oben dargelegten Sinne ein musikalisches Modell (z.B. eine Quintfallsequenz) und unter ›Objekt‹ eine spezifische musikalische Wendung (z.B. bei Bach oder Händel) verstanden wird, lässt sich der Beginn dieses Absatzes wie folgt formulieren: Der Begriff ›Quintfallsequenz‹ ist in der musikalischen Analyse ein abstrakter Oberbegriff, der die gemeinsame Struktur und das gemeinsame Verhalten von spezifischen musikalischen Wendungen z.B. im Werk von Bach oder Händel beschreibt.

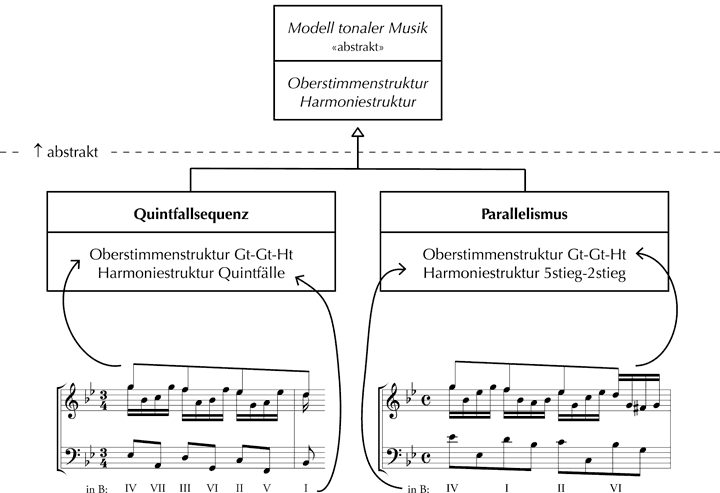
Einen wichtigen Bestandteil der Objektorientierung bilden sogenannte ›abstrakte Klassen‹. Die Bezeichnung ›abstrakt‹ irritiert auf den ersten Blick, weil im Vorangegangenen bereits die Klasse als abstrakter Oberbegriff für Objekte definiert worden ist. Der Hauptunterschied zwischen einer ›Klasse‹ und einer ›abstrakten Klasse‹ liegt darin, dass letztere keine Objekte erzeugen kann bzw. sich nicht instanzieren lässt. Nehmen wir an, für die musikalische Analyse wäre eine abstrakte Klasse ›Modell tonaler Musik‹ zu konstruieren, dann könnte diese Klasse die Deklarationen z.B. einer strukturellen Oberstimme, einer Harmoniestruktur etc. enthalten, also Deklarationen von Eigenschaften, die sich üblicher Weise an Modellen tonaler Musik beobachten lassen. Die abstrakte Klasse ›Modell tonaler Musik‹ wird jedoch nur dann Gültigkeit für verschiedene Modell-Klassen beanspruchen dürfen, wenn die in ihr vorgenommenen Deklarationen abstrakt, das heißt nicht als spezifische Eigenschaften definiert werden, da verschiedene Modelle verschiedene Oberstimmen-, Bassstimmen- und Harmoniestrukturen etc. aufweisen. Modell-Klassen wie ›Quintfallsequenz‹ oder ›Parallelismus‹ könnten wiederum die von der abstrakten ›Modellklasse tonaler Musik‹ deklarierten Eigenschaften ›erben‹, was bedeutet, dass eine Verpflichtung bestände, die abstrakt deklarierten Eigenschaften zu implementieren und mit spezifischen Werten zu belegen bzw. zu überschreiben.[6] Abb. 1 veranschaulicht den Sachverhalt durch ein Klassendiagramm:[7]

Abb. 1: Klassendiagramm für die Modell-Klassen ›Quintfallsequenz‹ und ›Parallelismus‹

Beide Modell-Klassen ›Quintfallsequenz‹ und ›Parallelismus‹ überschreiben die Eigenschaft Oberstimmenstruktur der abstrakten Klasse ›Modell tonaler Musik‹ auf gleiche Weise (Oberstimmenstruktur Ganzton-Ganzton-Halbton), während die Eigenschaft Harmoniestruktur auf unterschiedliche Weise implementiert wird (zum einen Quintfälle, zum anderen eine sequenzielle Folge von Quint- und Sekundstiegen). Darüber hinaus wäre es in den abgeleiteten Klassen möglich, weitere Eigenschaften zu definieren, die nicht auf Vererbung beruhen.

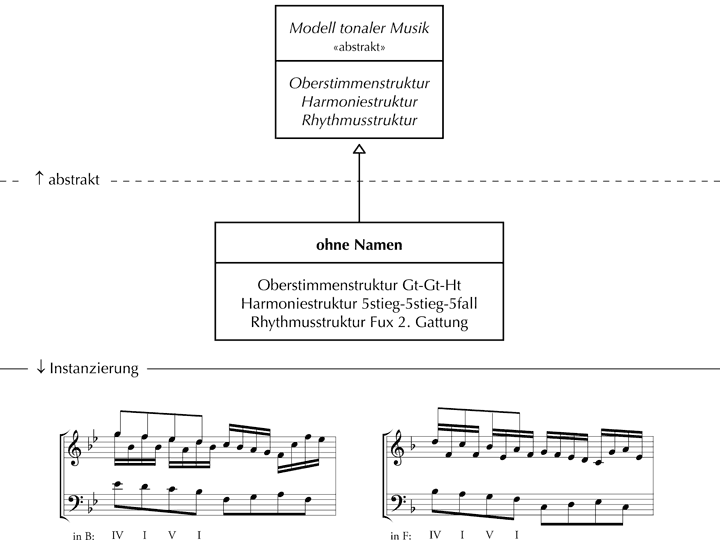
Zu einer Modell-Klasse (oder vereinfacht: zu einem Modell) tonaler Musik werden die genannten sowie weitere Parameter gezählt, nicht jedoch individuelle Merkmale des konkreten kompositorischen Kontextes wie z.B. die Tonart B-Dur eines spezifischen Werkes. Deswegen lässt sich ein Modell (z.B. ein Parallelismus) in den Werken von Schubert, Mozart oder Bach beobachten (bzw. instanzieren) und zwar unabhängig von Tonart bzw. Taktart der jeweiligen Komposition. Für eine konkrete Instanz sind dabei alle deklarierten Eigenschaften eines Modells – also auch Oberstimmen- und Harmoniestrukturen – mit Werten zu belegen (z.B. ›g-f-es-d‹ als Wert der Oberstimmenstruktur Gt-Gt-Ht).[8] Abb. 2 veranschaulicht eine Klassenhierarchie sowie die Instanzierung einer Modell-Klasse in unterschiedlichen tonalen Kontexten (B-Dur und F-Dur).

Abb. 2: Instanzierung einer Klasse in unterschiedlichen tonalen Kontexten

Abb. 2 macht zudem deutlich, dass sich in komponierter Musik Instanzen von Modell-Klassen aufzeigen lassen, die zwar durch charakteristische Eigenschaften ausgewiesen sind, für die jedoch kein Begriff existiert (angesichts der wenigen etablierten Fachbegriffe im Rahmen wissenschaftlichen Analysierens wahrscheinlich der Regelfall). In meiner Arbeit Die Notenbücher der Mozarts habe ich die abgebildete Modell-Klasse als ›IV-I-V-I-Pendelmodell‹ bezeichnet[9], Robert Gjerdingen subsumiert sie in seinem Buch Music in the Galant Style unter dem Namen ›Prinner‹ (zum Angedenken an den 1624 geborenen und 1694 gestorbenen Musikpädagogen Johann Jacob Prinner).[10] Dem Modell folgt ein Halbschluss.[11] An dieser Stelle sei noch einmal hervorgehoben, dass es üblich ist, transponierte musikalische Wendungen als Instanzen derselben Modellklasse zu interpretieren, weil diese Art der Transformation in der musikalischen Analyse als Operation angesehen wird, welche die wesentlichen Eigenschaften eines Modells nicht berührt.

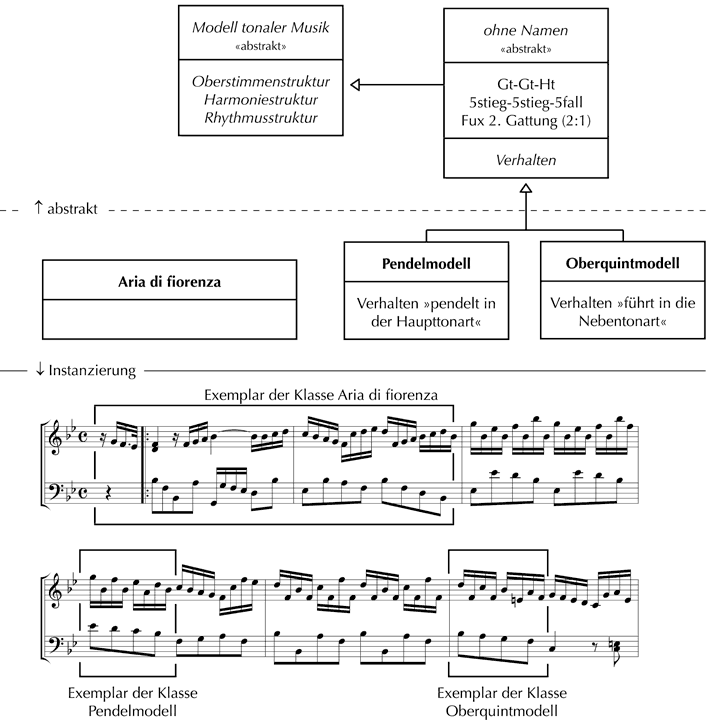
Die beiden oben abgebildeten Wendungen in B-Dur und in F-Dur entstammen im Original nicht zwei verschiedenen, sondern einer einzigen Komposition, nämlich der Allemande in B-Dur (G 30) von Georg Friedrich Händel (Abb. 3). Nach einer Eröffnung durch eine zweitaktige Instanz einer Modell-Klasse, die ich in Anlehnung an eine Arbeit von Warren Kirkendale als ›Aria di fiorenza‹[12] bezeichne und die bei Gjerdingen unter dem Namen ›Romanesca‹[13] firmiert (= erster ›Absatz‹ im Sinne einer paradigmatischen Kadenzfolge nach Heinrich Christoph Koch), erklingt eine zweite – in der Abbildung unbenannte – Taktgruppe in der Subdominante sowie im Anschluss daran das oben abgebildete IV-I-V-I-Pendelmodell mit dem Halbschluss in B-Dur (= zweiter ›Absatz‹ einer paradigmatischen Kadenzfolge nach Koch). Diesen Gestaltungen folgen die Unterquarttranspositionen der zweiten Taktgruppe sowie des IV-I-V-I-Pendelmodells mit Halbschluss (= dritter ›Absatz‹ einer paradigmatischen Kadenzfolge im Sinne Kochs). Das hier nicht wiedergegebene Ende des ersten großen Formteils der Allemande bildet ein Ganzschluss in F-Dur (= vierter Gliederungspunkt bzw. Schlusssatz nach Koch). Durch die Tatsache, dass die zwei Exemplare des in Abb. 2 gezeigten Pendelmodells nicht in verschiedenen Kompositionen, sondern in einer einzigen auftreten, wird ein Problem offensichtlich: Obgleich die Modelle im vierten und sechsten Takt bis auf den tonalen Kontext identisch sind, hören wir die erste Passage als Bestätigung der Grundtonart B-Dur (S → T), die zweite dagegen als Hinführung zur Dominante (T → D) bzw. Modulation in die Tonart der V. Stufe. Die Modelle wirken also trotz gleicher Satztechnik aufgrund der jeweiligen formalen Position und Transposition verschieden. Abb. 3 trägt dem genannten Höreindruck durch eine Erweiterung des Klassendiagramms Rechnung.

Abb. 3: Georg Friedrich Händel, Allemande in B-Dur (G 30)

Die abstrakte Superklasse ›Modell tonaler Musik‹ deklariert die Eigenschaften Oberstimmen-, Harmonie- und Rhythmusstruktur. Von einer abstrakten Modell-Klasse ›ohne Namen‹ werden diese Eigenschaften implementiert und mit spezifischen Werten versehen (Oberstimmenstruktur = Ganzton-Ganzton-Halbton, Harmoniestruktur = Quintstieg-Quintstieg-Quintfall sowie Rhythmusstruktur = Fux: 2. Gattung (2:1)). In dieser Form entspricht die abstrakte Subklasse dem Bauplan eines ›Satzmodells‹ im herkömmlichen Sinne. Darüber hinaus enthält die Klasse ›ohne Namen‹ ein abstrakt deklariertes ›Verhalten‹, das der Beschreibung dient, welche Funktion dem Modell im Kontext einer tonalen Komposition zukommt. Sowohl die bereits konkret implementierten Eigenschaften als auch das abstrakt deklarierte Verhalten der Klasse ›ohne Namen‹ werden nun den Subklassen ›Pendelmodell‹ und ›Oberquintmodell‹ vererbt. Die abgeleitete Pendelmodell‹-Klasse erhält durch Vererbung also die konkreten Eigenschaften für Oberstimmen-, Harmonie- und Rhythmusstrukturen[14] sowie die Verpflichtung zur Implementierung eines spezifischen Verhaltens, das sich z.B. in dem Sinne formulieren ließe, dass von ihr erzeugte Objekte das Gefühl für die Tonart durch ein harmonisches ›IV-I-V-I-Pendeln‹ festigen. In der Subklasse ›Oberquintmodell‹ hingegen könnte das Verhalten beschrieben werden als: ›Führe in den Bereich der Nebentonart vermittels einer I-V-II#-V-Harmoniefolge‹ (also das Verhalten eines Modulationsmodells im traditionellen Sinne).

Aus dem Gesagten ergeben sich weitreichende Konsequenzen, und ich finde es interessant, dass der aus der Informatik geborgte Denkansatz der Objektorientierung in der Lage ist, methodisch sauber die Überreste einer positivistischen Musiktheorie zu entsorgen. Denn auf der untersten Ebene der Vererbungshierarchie wurde in Abb. 3 mit zwei verschiedenen Modellen operiert (›Pendelmodell‹ und ›Oberquintmodell‹), die wir im Rahmen einer herkömmlichen Parameteranalyse (bzw. im Sinne von ›Satzmodellen‹) als vollkommen identisch bezeichnen müssten.

Der Umstand, dass zwei von einer Superklasse abgeleitete Subklassen ein abstrakt deklariertes und vererbtes Verhalten auf verschiedene Weise implementieren, was zu einem unterschiedlichen Verhalten ihrer Objekte führt, wird in der OOP als ›Polymorphie‹ bezeichnet.[15] Findet dieses Konzept nicht nur auf ein Verhalten, sondern auch auf Eigenschaften Anwendung (z.B. auf die Eigenschaft ›Harmoniestruktur‹), lassen sich als Ergebnis nicht nur aufgrund unterschiedlichen Verhaltens unterschiedliche Modelle mit gleichen Eigenschaften, sondern auch gleiche Modelle aufgrund gleichen Verhaltens mit unterschiedlichen Eigenschaften denken. Beide Fälle sind in der musikalischen Analyse sinnvoll, denn es ermöglicht nicht nur, Modelle bei gleicher Satztechnik aufgrund ihres unterschiedlichen Verhaltens zu unterscheiden, sondern auch zwei musikalische Passagen als gleich zu identifizieren (z.B. als ›Oberquintmodell‹), weil sie sich in kompositorischen Kontexten in gleicher Weise verhalten (z.B. von der Grundtonart in die Oberquinte führen), obwohl sie z.B. eine differente Harmonik aufweisen (also in einem positivistischen Sinne ›verschieden‹ sind).[16]

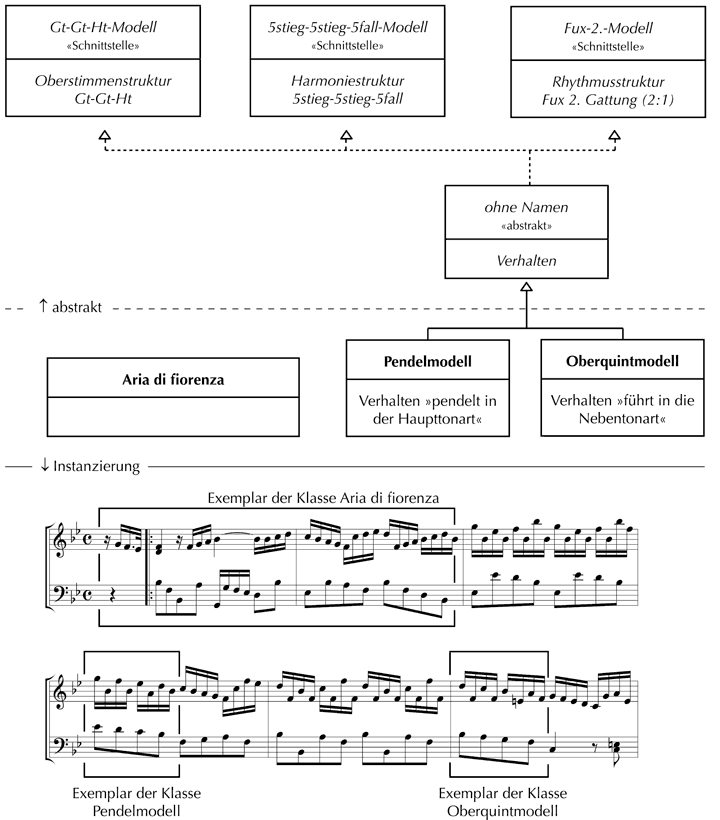
Das bisher entworfene Klassendesign könnte abschließend durch ein wichtiges Konzept moderner objektorientierter Programmiersprachen erweitert werden, nämlich das Konzept sogenannter Schnittstellen.[17] Schnittstellen dienen der Deklaration von Vereinbarungen, an die sich alle Klassen halten müssen, welche die jeweilige Schnittstelle implementieren. Eine Schnittstelle beispielsweise, von der die Eigenschaft ›hat Saiten‹ definiert und die von der Klasse Streichinstrumente implementiert wird, verpflichtet alle Streichinstrumente dazu, Saiten zu haben. Die gleiche Schnittstelle kann zudem ›Vertragspartner‹ verschiedener Klassen sein. Es wäre z.B. sinnvoll, wenn auch die Klasse Zupfinstrumente eine vertragliche Verpflichtung mit der Schnittstelle ›hat Saiten‹ eingehen und somit Zupfinstrumente verpflichten würde, Saiten zu haben. Das Auslagern von ›hat Saiten‹ wird dabei in der Objektorientierung als ›Kapselung‹ bezeichnet. Der Vorteil gekapselter Eigenschaften liegt darin, dass diese von den implementierenden Klassen unabhängig gedacht werden können: z.B. ist die Eigenschaft ›hat Saiten‹ unabhängig von den Klassen ›Streichinstrumente‹ und ›Zupfinstrumente‹ und steht daher (als Schnittstelle) auch für eine Klasse ›Klavierinstrumente‹ zur Verfügung. In Bezug auf das bisher entworfene Modell-Klassendesign wäre es daher möglich, die in der abstrakten Klasse ›ohne Namen‹ implementierte Oberstimmenstruktur ›Ganzton-Ganzton-Halbton‹, die Harmoniestruktur ›Quintstieg-Quintstieg-Quintfall‹ sowie die Rhythmusstruktur ›Fux: 2. Gattung (2:1)‹ zu kapseln bzw. in Schnittstellen auszulagern. Der Vorteil läge in der Kombinierbarkeit (und hinsichtlich der Programmierung in der Wiederverwendbarkeit) der genannten Eigenschaften für alle erdenklichen Modell-Klassen tonaler Musik.

Abb. 4: Kapseln konkreter Eigenschaften mit Hilfe von Schnittstellen

Bevor ich auf die Art des Instanzierens in einer musikalischen Analyse eingehen und verschiedene Probleme ansprechen werde, seien zuvor noch einige klärende Überlegungen zum Begriff des Verhaltens gestattet. Wie bereits erwähnt, ist unter dem Verhalten eines Modells seine spezifische Funktion innerhalb einer bestimmten Komposition zu verstehen. Während sich Eigenschaften also direkt an einer Modellinstanz beobachten lassen, ist eine Bestimmung des Verhaltens nur über den kompositorischen Kontext möglich. Die denkbaren Funktionen eines Modells in einer Komposition fallen dabei weder mit den harmonischen Funktionen ›Tonika‹, ›Subdominante‹ und ›Dominante‹ (Hugo Riemann) noch mit den Formfunktionen ›Vordersatz‹, ›Fortspinnung‹, ›Epilog‹ (Wilhelm Fischer) bzw. ›Presentation‹, ›Continuation‹ und ›Cadential‹ (William Caplin) zusammen. Das Denken in den elementaren Formfunktionen ›Anfang‹, ›Mitte‹ und ›Ende‹, das nicht erst von Fischer und Caplin beschrieben worden ist, sondern bereits in der Improvisations- und Kompositionsdidaktik des 18. Jahrhunderts Konjunktur hatte[18], stellt zwar für die Analyse nützliche Verhalten bereit, die Beschränkung auf eine bestimmte Anzahl von Formfunktionen bzw. Verhaltensweisen wäre jedoch dogmatisch und speziellen Interessen verpflichtet. In meiner Arbeit Die Notenbücher der Mozarts habe ich dem ›Verhalten‹ (bzw. der Formfunktion) darüber hinaus die Kategorien ›Inszenierungsweise‹ und ›Ausdehnung‹ an die Seite gestellt (im Sinne abstrakter Superklassen-Deklarationen). Mit der Verpflichtung, die Ausdehnung eines Modells hinsichtlich seines Kontextes zu beschreiben, lässt sich vergegenwärtigen, dass in der Analyse üblicher Weise nicht konkrete musikalische Erscheinungen, sondern deren musiktheoretische Abstraktionen verglichen werden. Die Aussagefähigkeit der Gleichheit von I-V-I-Harmoniefolgen ist daher gering, wenn einmal eine Kadenzwendung, ein anderes Mal eine Taktgruppenharmonik und ein drittes Mal ein Satzverlauf beschrieben wird. Über die Kategorie ›Inszenierungsweise‹ lassen sich zudem standardisierte musikalische Gesten wie z.B. ein rauschendes Orchestertutti als Abschluss eines größeren Formteils oder ein bassloses Register mit solistischen Bläserfarben an der Position eines Seitensatzes oder Seitenthemas benennen, wobei spezifische Inszenierungsweisen die Wirkung gleicher Satztechniken so grundlegend verändern können, dass es sinnvoll erscheint, in solchen Fällen von unterschiedlichen Modellen zu sprechen.

Die Akte der Instanzierung, nicht jedoch die Vorgänge des Instanzierens lassen sich in der Computerwelt und im Rahmen einer musikalischen Analyse vergleichen. Während das Konzept der Objektorientierung in der Computerwelt dadurch aufgelöst wird, dass eine triviale Maschine[19] (Compiler) einen ausführbaren Maschinencode erzeugt, der eine Äquivalenz zum modellierten Programmdesign darstellt, erfolgt das Instanzieren von Modellen im musiktheoretischen Kontext in Form von Beobachtungen an einer Komposition durch Nicht-Trivialmaschinen (Menschen). In Anlehnung an einen »extrem formalen Begriff des Beobachtens«[20] wird hier unter Beobachtung das Benutzen einer Unterscheidung sowie das Bezeichnen des Unterschiedenen verstanden. In der Allemande von Händel beispielsweise wurden die ersten beiden Takte vom Rest der Komposition unterschieden und für ihre Bezeichnung der Begriff ›Aria di fiorenza‹ gewählt. Die Operation des Beobachtens (bzw. Unterscheidens und Bezeichnens) fällt dabei mit dem Akt der Instanzierung zusammen, das durch den Begriff Bezeichnete repräsentiert die Instanz einer entsprechenden Modell-Klasse.

Beobachtungen dieser Art sind stark wissensgeleitet und widersprechen dem gelegentlich anzutreffenden Anspruch, die Art des Beobachtens in der musikalischen Analyse müsse »möglichst unvoreingenommen« erfolgen.[21] Diese Forderung dürfte dem Bemühen geschuldet sein, Beschreibungen nicht von vornherein musiktheoretischer Dogmatik auszuliefern. Doch der Versuch, Musik so beobachten zu wollen, wie sie ist (und nicht so, wie sie nicht ist), setzt die ontologische Sein-Nichtsein-Unterscheidung voraus und zwingt zu einem Realitätsverständnis aus der Perspektive des Subjekt-Objekt-Schemas. Abgesehen von den erkenntnistheoretischen Problemen, die hierbei zwangsläufig mitgeschleppt werden, verschleiert die Forderung nach Unvoreingenommenheit den Widerspruch zwischen der Freiheit, die hinsichtlich der zahlreichen Beschreibungsmöglichkeiten eines Gegenstandes nach Aufhebung der Limitation durch Voreingenommenheit existiert, und den Zwängen der Kausalität, die mit Kommunikationsabsichten, Unterrichts- und Lernzielen einhergehen. Die Forderung nach Unvoreingenommenheit dürfte also schon allein deshalb scheitern, weil das Beobachten der Forderung nach Unvoreingenommenheit selbst Voreingenommenheit erzeugt.

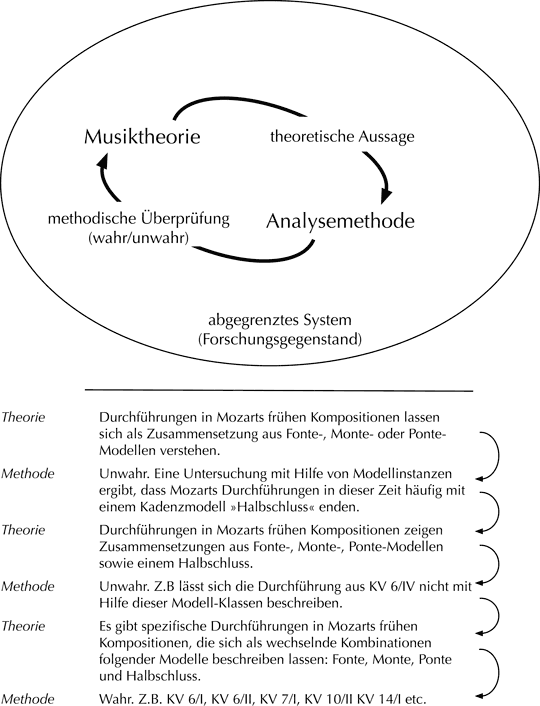
Wird die Forderung nach einer möglichst unvoreingenommenen Beschreibung zurückgewiesen, bedeutet dies zugleich einen Versuch preiszugeben, den Einfluss musiktheoretischer Dogmatik im Rahmen einer musikalischen Analyse zu kontrollieren. Es bleibt daher die Frage, auf welche Art sich eine musikalische Analyse, die den Anspruch auf Wissenschaftlichkeit erhebt, vom kultischen Gebrauch einer analytischen Methode unterscheiden lässt, zumal auch für wissenschaftliche Fragestellungen Begrenzungen notwendig sind, ohne die sich jede Untersuchung ins Unendliche verlieren würde. Als Antwort sei auf Luhmanns Unterscheidung zwischen ›Theorie‹ und ›Methode‹ verwiesen. Nach dieser Unterscheidung sind Methoden ›Programme‹, die einem binären Code verpflichtet sind und kein anderes Ziel haben als »eine Entscheidung zwischen wahr und unwahr herbeizuführen«.[22] Diese Programme befinden sich in strikter Koppelung mit Theorien bzw. anders gearteten ›Programmen‹, die spezifizieren, unter welchen Bedingungen die Qualifikation ›wahr‹ oder ›unwahr‹ erfolgt. Theorien, die der binären Codierung nicht unterworfen sind, bestehen aus Aussagen in Form von Sätzen, die sich auf etwas anderes als sich selbst beziehen (z.B. auf einen Untersuchungsgegenstand, Luhmann spricht in diesem Zusammenhang von ›assoziierter Fremdreferenz‹ bzw. einer ›eingebauten Asymmetrie‹).[23] Das Zusammenspiel von Theorie und Methode wird sehr pragmatisch erläutert:

Beide Arten von Programmen können unter wie immer willkürlichen und vorläufigen Limitierungen in Operation gesetzt werden, da jede Limitation von der anderen Seite der Unterscheidung her infrage gestellt und gegebenenfalls ausgewechselt werden kann. Limitation ohne Limitation also! Die Theorien können ausgewechselt werden, je nachdem, was ihre methodische Überprüfung ergibt. Und die Methoden werden gewählt, korrigiert und gegebenenfalls weiterentwickelt je nach dem, was man zur Überprüfung von Theorien braucht […].[24]

Um Missverständnissen vorzubeugen sei erwähnt, dass Luhmann mit der Formulierung »wie immer willkürlich«[25] kein ›vollkommen beliebiges‹ In-Operation-Setzen von Theorie und Methode meint:

Man formuliert nicht aufs Geratewohl Sätze, um dann sich um die Feststellung ihrer Unwahrheit zu bemühen. Die festzustellende Unwahrheit muß ›interessant‹ sein, muß also im Falle ihrer Wahrheit eine sinnvolle Theorie ergeben. Andernfalls wäre alles möglich und das System hätte an seiner Struktur nicht genügend Führung […].[26]

Daher wird für den Beginn eines Theorieaufbaus empfohlen:

Sicher ist die einfachste Auskunft eine rein historische: Man arbeitet mit den Unterscheidungen, die sich schon bewährt haben und deren Kondensate die Formulierungen von Theorien ermöglichen, die ihrerseits Erkenntnisse festhalten, die man für wahr hält.[27]

Abb. 5: Wissenschaft als strikte Koppelung der Programme ›Theorie‹ und ›Methode‹

In Anknüpfung an das theoretische Werk Joseph Riepels und daran orientierten Forschungsarbeiten zeigt Abb. 5 ein exemplarisches In-Gang-Setzen von Theorie und Methode im Bereich musikalischer Analyse. Damit dürfte niemandem, der heute dieses Geschäft ernsthaft betreibt, wirklich etwas Neues gesagt sein. Doch hinsichtlich eines noch zu etablierenden wissenschaftlichen Fachs, bei dem das Wort ›Theorie‹ im Namen so ernst genommen wird, dass Musiktheorie nicht nur als historische, sondern auch systematische Disziplin verstanden wird, könnte es von Bedeutung sein zu vergegenwärtigen, was aus der dargelegten Perspektive die Kriterien der Wissenschaftlichkeit nicht erfüllt: Das Bestimmen von Modellinstanzen, Chiffrieren von Akkordfunktionen, Benennen von Stufenfolgen, Konstruieren von Stimmführungszügen, Operieren mit Tonfeldern etc. – es sei denn, das bisher bekannte methodische Arsenal der Musiktheorie wäre in den Dienst der Qualifizierung (wahr/unwahr) theoretischer Sätze gestellt (z.B. in der Form: »spezifische Expositionen des Komponisten x aus den Jahren y lassen sich als Ausprägung der Modellkombination z verstehen« oder allgemeiner »Musik ab x lässt sich angemessen als spezifische Abfolge y der Tonfelder z beschreiben« etc.). Selbst die kapriziöse Beherrschung analytischer Methoden wäre demnach Propädeutik (in einem positiven Wortsinn), das Operieren mit theoretischen Sätzen ohne methodische Überprüfbarkeit[28] (z.B. das Konstatieren von Komponistenintentionen) allenfalls Bestandteil eines didaktischen Designs zur Erweckung von Motivation (im Unterricht). Spezifisch wissenschaftliche Leistungen wären letztendlich daran zu bemessen, ob es gelingt, die Abstraktion der Vergleichsgesichtspunkte so weit voranzutreiben, dass »auch evident Ungleiches verglichen werden kann (und nicht nur der Erfüllungsgrad von Wünschen gemessen wird)«.[29]

Abschließend sei die Frage nach der Bedeutung des zu Beginn dargelegten Modell-Konzepts im Rahmen einer wissenschaftlichen musikalischen Analyse gestattet. Das Instanzieren (bzw. Beobachten) eines Modells ist eine beobachtbare Operation, das Vergegenwärtigen einer Modellklasse im objektorientierten Sinn Resultat dessen, was von Luhmann als Wechsel des Beobachters oder als Anweisung »an eine Beobachtung von Beobachtern« bezeichnet worden ist.[30] Nur die Reflexion dessen, was als Modell instanziert wurde (und warum), garantiert die Möglichkeit der gezielten Entwicklung neuer Modelle. Die Rhythmusstruktur ›Fux 2. Gattung (2:1)‹ beispielsweise wäre als konstitutive Eigenschaft für Pendel- und Oberquintmodelle wenig geeignet, denn sie ermöglicht bestenfalls eine Bewahrheitung theoretischer Aussagen zu einer spezifischen musikalischen Stilistik aus der ersten Hälfte des 18. Jahrhunderts. Wird diese Eigenschaft jedoch vernachlässigt, qualifiziert sich das Modell auch für die Beschreibung der Musik Mozarts bzw. zur Bewahrheitung von Aussagen über nicht stilgebundene Entwicklungszüge tonaler Musik (z.B. Aussagen zur Entwicklung der Sonatenhauptsatzform, wofür im Übrigen auch die nach Koch stimmige Absatzdisposition als Indiz gewertet werden könnte). Die Verpflichtung zur Einhaltung des beständigen Perspektivwechsels (zwischen Beobachtungen erster und zweiter Ordnung) ist unabdingbare Voraussetzung für die Ausbildung einer Methodologie und Entwicklung der Analyse nach Modellen jenseits von ›Parallelismus, Quintfallsequenz & Co‹. Nicht zuletzt wäre ein solcherart differenziertes Denken von Modellen geeignet, wenig ergiebige Fachgespräche zu vermeiden, weil sich schnell vergegenwärtigen ließe, ob beim Verwenden gleicher Begriffe gleiche Modelle benannt werden und ob Theorieprogramme unterschieden (oder gar nicht vorhanden) sind, wodurch sich wiederum eine Diskussion über die Unterschiedlichkeit (oder Beliebigkeit) von Modellen erübrigt.

Über die eingangs gestellte Frage ›Was ist ein musikalisches Modell?‹ wurde ein an der Objektorientierung angelehntes Denken musikalischer Modelle für tonale Musik erläutert sowie der Versuch unternommen, dieses Denken in einem an Luhmanns Ausführungen orientierten Wissenschaftskonzept zu verorten. Damit dürften allerdings mehr Fragen aufgeworfen denn beantwortet sein, z.B.: Wie müssten Analysemethoden für eine Musik beschaffen sein, die nicht unter das ästhetische Paradigma einer ›ars combinatoria‹ (im weitesten Sinne) fällt und die sich gegen das hier dargelegte Analysieren nach Modellen sperrt? Welche Arten theoretischer Sätze sind über eine Musik möglich, die einen Komplexitätsgrad aufweist, der viele musikalische Erscheinungen des 20. und 21. Jahrhunderts kennzeichnet? Und auf welche Weise müssen theoretische Sätze und Methoden hinsichtlich einer Musik vorgestellt werden, deren Beschreibung sich traditioneller Analyse am Notentext weitgehend entzieht (z.B. hinsichtlich einer mit Hilfe von hoch-komplexer Studiotechnik gefertigten Populären Musik)? Um den hier vorgestellte Ansprüchen an wissenschaftliches Arbeiten genügen zu können, dürfte das Entwickeln theoretischer Fragestellungen sowie geeigneter Analysemethoden zu den größten Herausforderungen für Fachvertreterinnen und Fachvertretern gehören, die den systematischen Aspekt des Fachs Musiktheorie nicht einer einseitig historischen Betrachtungsweise zu opfern gewillt sind.