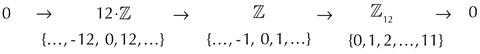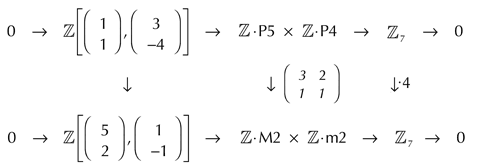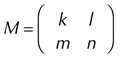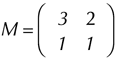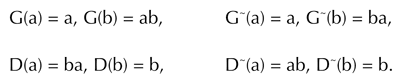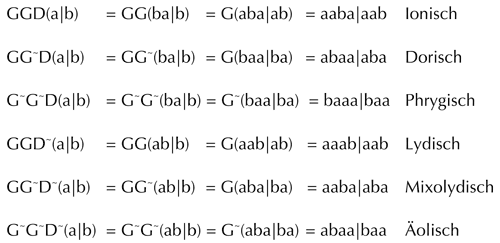Die Vernunft in der Tradition: Neue mathematische Untersuchungen zu den alten Begriffen der Diatonizität[1]

Während seit Jahrzehnten in Deutschland das Interesse der Systematischen Musikwissenschaft an der Suche nach mathematischen Begründungen musiktheoretischer Gegebenheiten nahezu erloschen scheint, bildet sich auf beiden Seiten des Atlantik eine Mathematische Musiktheorie als Spezialdisziplin heraus, die sich unter neuen Vorzeichen jener beinahe aufgegebenen Herausforderung stellt.

Mit dem Gründungskongress der Deutschen Gesellschaft für Musiktheorie im Jahre 2001 unter dem Motto »Musiktheorie zwischen Historie und Systematik« wurden die Weichen grundsätzlich in Richtung Integration gestellt, und so ist es an der Zeit, anhand der inzwischen erzielten Resultate auch einen gewissen Ausgleich zu suchen zwischen den gedämpften Erwartungen einer breiten Mehrheit von Musikwissenschaftlern und Musiktheoretikern auf der einen Seite und der Zuversicht der ›autonomen‹ mathe-musikalischen Widerständler auf der anderen. Das Projekt einer Integration des unter verschiedenen Perspektiven gewonnenen Wissens, schließt die Aufgabe ein, auch das Selbstverständnis der Musiktheorie und ihres Gegenstandsbereiches zu reflektieren, den sie sich heute mit künstlerischen, historisch-philologischen und systematisch-logischen Zugangsweisen erschließt.

Die Beschäftigung mit dem musiktheoretischen Vermächtnis von Carl Dahlhaus ist daher ein willkommener Anlass, einen Beitrag zur Auflösung jenes ambivalenten Verhältnisses der Musikwissenschaft gegenüber Mathematisierungsansätzen innerhalb der Musiktheorie zu leisten und Erfüllungsbedingungen für systematische Untersuchungen an tradierten musiktheoretischen Begriffen zu formulieren. Im Bewusstsein um die Schwierigkeit der ontologischen Verankerung und der epistemologischen Bewertung solcher Untersuchungen gilt es, geeignete Zugänge zur Begriffsanalyse als Erkenntnisquelle freizulegen und gegenüber einschlägigen Bedenken und Einwendungen zu behaupten und zu begründen.

Als Leitbild für das Erschließen von historischen Begriffen als Erkenntnisquelle für neue systematische Überlegungen dient die enge Verwobenheit historischer und systematischer Argumentationsstränge in Carl Dahlhaus’ Untersuchungen über die Entstehung der harmonischen Tonalität.[2] Dieser Text fungiert zugleich als Brennglas für den musiktheoretischen Diskurs jener ›alten Schule‹ eines historisch verankerten Systematisierens von Begriffen der Diatonizität.[3] Als ein wichtiger argumentativer Bezugspunkt für Dahlhaus’ Auseinandersetzung mit dem Gebiet der Musiktheorie gehört hierzu Jacques Handschins Abhandlung Der Toncharakter. Eine Einführung in die Tonpsychologie.[4] Dies betrifft nicht nur inhaltliche Fragen, sondern auch die wissenschaftspolitische Einordnung der Musiktheorie durch den Handbuchautor und -herausgeber Dahlhaus.

Der vorliegende Aufsatz ist in vier Abschnitte gegliedert. Die Darstellung und Diskussion der musiktheoretischen Inhalte sind den Abschnitten 2–4 vorbehalten, wogegen der erste Abschnitt einige Schlaglichter auf den Theoriebegriff und die Diskussion um die Legitimität oder Illegitimität abstrakter mathematischer Untersuchungen von musiktheoretischen Begriffen werfen soll.

Ausgehend von der Leitidee hinter Handschins Begriff des ›Toncharakters‹ macht im zweiten Abschnitt eine Synopsis von Erkenntnissen aus der Diatonic Set Theory mit der Herangehensweise der formalen Begriffsanalyse vertraut. Dort steht ein systematisches Erkenntnisinteresse im Mittelpunkt und die Ideengeschichte der Begriffe wird ausgeblendet. Die Untersuchung richtet sich vielmehr auf die Feststellung von logischen Abhängigkeiten von Begriffen untereinander.

Schließlich wird in den Abschnitten 3 und 4 der Versuch unternommen, eine Interpretation der mathematischen Erkenntnisse im Lichte tradierten musiktheoretischen Wissens vorzunehmen und dabei an bestimmte Formen musiktheoretischen Argumentierens bei Dahlhaus anzuknüpfen. Neben der eigentlichen Auseinandersetzung mit den Inhalten sollen anhand dieser beiden Abschnitte auch Beispiele gegeben werden für die Integration mathematischer Untersuchungen in eine musiktheoretische Forschung, die ihr Wissen zwischen Historie und Systematik unter neuen Gesichtspunkten ordnet und erweitert.

1. Neue alte Musiktheorie und die Rolle der Mathematik

Das geschichtsträchtige und damit nicht ganz unbelastete Verhältnis zwischen Mathematik und Musik hat einen nicht unwesentlichen Einfluss auf die kontrovers diskutierte Frage nach den Gegenständen und Erkenntnismethoden der Musiktheorie. Um heute die Erfüllungsbedingungen für eine erfolgreiche Anwendung mathematischer Methoden in der Musiktheorie zu reflektieren, gilt es deshalb eine Hürde zu nehmen, welche durch die ambivalente Haltung der Systematischen Musikwissenschaft gegenüber der Musiktheorie errichtet wird.

Unter Berücksichtigung einer aufschlussreichen Diagnose von Ludwig Holtmeier (2004) könnte man versucht sein, jene Hürde als das Phantom eines inzwischen verblassten Zeitgeistes zu deuten:

Die deutsche musiktheoretische Antisystematik hat eine lange Tradition. Ihre Wurzeln dürften im antirationalistischen Aufbruch der ›Lebensreform‹ der [19]10er und [19]20er Jahre zu suchen sein. In den [19]30er Jahren ist es ein Signum der deutschen Musiktheorie, daß sie sich ihrer selbst schämt. Seit dieser Zeit bemüht man sich zu betonen, daß Musiktheorie keine ›Theorie‹ sei.

Es ist eine Stärke der deutschen Musiktheorie, daß sie ›autonomistischen‹ Systemen reserviert gegenübersteht. Aber es scheint, als habe gerade die lebensphilosophische Angst, den unmittelbaren Bereich der Erfahrung zu verlassen, die Disziplin in Deutschland erstarren lassen. Tatsächlich hat sich die einst so fruchtbare Disziplin in den letzten 60 Jahren nur unwesentlich entwickelt.[5]

Mit dem Hinweis auf die Zurückhaltung gegenüber »autonomistischen Systemen« macht Holtmeier zugleich deutlich, dass die Aufbruchsbewegung der GMTH in seinen Augen keine bloße Hinwendung zu den orthodoxen systematischen Ansätzen der nordamerikanischen Musiktheorie bedeuten kann. Gleichwohl muss dann im Zuge eines solchen Aufbruchs bloße Reserviertheit – etwa gegenüber der Diatonic Set Theory der 1980er und 90er Jahre – in eine konstruktive kritische Auseinandersetzung münden. Ziel des vorliegenden Beitrags ist es deshalb, vor allem Interesse an solch einer Auseinandersetzung zu wecken. In diesem ersten Abschnitt sollen zunächst Vorbehalte ausgemacht, im überlieferten Diskurs beleuchtet und – zumindest teilweise – ausgeräumt werden.

Die Kluft, die es zu überwinden gilt, liegt zwischen dem Bedürfnis nach gesicherter Erkenntnis auf der einen Seite und einem ontologischen Vakuum auf der anderen, welches im traditionellen Kerngebiet der Musiktheorie nach der antidogmatischen Reform der letzten Jahrzehnte entstanden ist. Die systematische Musikwissenschaft meidet dieses Vakuum und verankert ihre Forschungen in den physikalischen, psychophysischen, neurologischen, kognitiven und sozialen Realitätsebenen von Musik. Offen ist, ob sich die systematische Musiktheorie in diesem transdisziplinären Arbeitsgebiet auflöst oder ob sie sich darin als eigenständige Disziplin erfolgreich weiterentwickelt. Ausschlaggebend dafür dürfte wiederum die Relevanz des in der Tradition erworbenen theoretischen Wissens für die an der wissenschaftlichen Erforschung von Musik beteiligten Disziplinen sein. Angesichts dieser Sachlage lohnt es durchaus den Versuch, eine Integration neuerer ›autonomistischer‹ mathematischer Untersuchungen mit der Aufarbeitung musiktheoretischer Traditionsbestände zu wagen.

Im Vorfeld wird nun an ausgewählten Beispielen rekapituliert, wie in den vergangenen Jahrzehnten verschiedene Perspektiven systematischer Musiktheorie thematisiert, entworfen bzw. auch verworfen werden und wie sich diese in der Ausrichtung bestimmter Strömungen manifestieren. Unter der Überschrift »Traditionsbestände der Systematischen Musikwissenschaft« äußert sich der Handbuchautor und Herausgeber Dahlhaus wie folgt:

Daß ›Theorie‹ im antiken Sinne – als ethisch inspirierte Kontemplation über ein durch Mathematik, und zwar platonisch-pythagoräisch interpretierte Mathematik, begründetes Tonsystem – seit Jahrhunderten nicht mehr existiert und daß die Schuldisziplin, die heute ›Theorie‹ heißt, nahezu das Gegenteil des antiken Begriffs, nämlich eine bloße Handwerkslehre darstellt, ist offenkundig und provozierte Jacques Handschins (1948) Unterscheidung zwischen ›Theoretikern‹ und ›Theorielehrern‹, schließt jedoch nicht aus, daß Teilmomente der Überlieferung, wenn auch in veränderter, verblaßter oder verzerrter Gestalt, im Kontext der modernen, am Kunstbegriff der Neuzeit orientierten Systematischen Musikwissenschaft überdauern. Die ›ästhetische‹ Kontemplation, die selbst- und weltvergessene Versenkung in ein Kunstwerk, kann ohne interpretatorischen Gewaltstreich als Umdeutung der ›ontologischen‹ Kontemplation und als Übertragung einer Anschauungsform vom Tonsystem auf das tönende Gebilde verstanden werden.[6]

Auffallend an dieser Stellungnahme ist das Fehlen eines Hinweises auf Verbindungen zwischen der überlieferten ›Theorie‹ im alten Sinne und neuen Formen der Theoriebildung. Jene Unterscheidung von alter Theorie und (damals) aktueller Handwerkslehre schließt ja nicht nur nicht aus, dass Teilmomente der Überlieferung im Rahmen der Ästhetik überdauern können. Ebenso könnten sie ihren Platz als Bestandteile einer erneuerten ›Theorie‹ beanspruchen. Die Missbilligung der »›ontologischen‹ Kontemplation« verweist auf eine ungünstige Verquickung von epistemologischen und ontologischen Grundhaltungen in der alten Theorie, aus deren Schatten eine erneuerte Theorie offenbar heraustreten müsste.

Einerseits gibt es die unleugbare Schwierigkeit, epistemologische Erfüllungsbedingungen für musiktheoretisches Forschen zu formulieren, insbesondere dann, wenn sie die für mathematische Untersuchungen typischen kontemplativen Höhenflüge in die ›dünne Luft der Abstraktionen‹ unternimmt. Andererseits zeugen die kritischen Reflexionen von Helga de la Motte-Haber und Peter Nitsche über die vielfältigen »Begründungen musiktheoretischer Systeme«[7] von der Schwierigkeit, die oftmals ontologisch motivierten musiktheoretischen Behauptungen überlieferter Theorieansätze als Wissensbestand der systematischen Musikwissenschaft anzuerkennen.

In einem früheren und inhaltlich sehr verwandten Text über die »Wandlungen des Theoriebegriffs« ist es Dahlhaus, der sich in dieser Hinsicht etwas deutlicher äußert:

Allerdings ist die für das 18. Jahrhundert charakteristische Wendung, daß sich die Bemühung um Theorie der Musik an das tönende Phänomen statt an abstrakte Strukturen heftete, nicht mehr rückgängig zu machen. Theorie der Musik kann heute nichts anderes als Theorie des konkreten musikalischen Gebildes, der Komposition und ihrer konstitutiven Momente sein. Doch muß, wenn Verwirrung vermieden werden soll, die Verquickung der Theorie mit Handwerkslehre ebenso gelöst werden wie die Abhängigkeit von der physikalischen Akustik. Statt von musikalischen Handwerksregeln auszugehen und – um der Legitimation als Theorie willen – für geschichtlich begründete Normen Scheinursachen in einer fiktiven Natur der Musik zu suchen, müßte die Theorie der Musik nach den Kategorien fragen, durch die sich eine Ansammlung akustischer Daten überhaupt erst als Musik konstituiert. Gegenstand einer so verstandenen Theorie, wie sie sich in Hugo Riemanns ›Lehre von den Tonvorstellungen‹ abzeichnet, sind die gestaltenden Prinzipien im musikalischen Bewußtsein. Versteht man Musik, nach Hanslicks Wort als »Arbeiten des Geistes in geistfähigem Material«, so ist es Ziel der theoretischen Reflexion, die Grundformen zu bestimmen, in denen der musikalisch sich verwirklichende Geist tätig ist.[8]

Diese teleologisch gefasste Bestimmung verortet die Musiktheorie – hier verstanden als Teilgebiet der systematischen Musikwissenschaft – in der Nähe der Musikkognition. Der angesichts neuester Entwicklungen noch an Aktualität gewonnene Reformvorschlag bringt die Frage mit sich, welche Traditionsbestände der Musiktheorie beim Auflösen jener Verquickung mit der Handwerkslehre in die erneuerte Theorie eingebracht werden, und in welcher Form dies geschehen kann. Müssen die auf unfesten ontologischen Fundamenten gegründeten Theoriegebäude konsequenterweise gänzlich in den Verantwortungsbereich der historischen Musikwissenschaft delegiert werden? Oder lassen sich Methoden finden, mit denen bewahrenswerte Traditionsbestände in einer geeigneten Form von systematisch geordnetem Wissen reformuliert werden können, um sie später gegebenenfalls auch in neuen Begründungszusammenhängen interpretieren zu können?

Anfang der 1980er Jahre ist die Haltung der Handbuchautoren ambivalent, und diese Ambivalenz spiegelt sich auch in der Gleichzeitigkeit dreier damals einsetzender und zunächst nur sparsam und kritisch miteinander kommunizierender Strömungen:

1. Ganz im Sinne von Dahlhaus’ Stellungnahme und damit auch in gewisser Erfüllung seines Vermächtnisses entwickelt die an den deutschsprachigen Musikhochschulen institutionalisierte Musiktheorie ein neues Selbstverständnis als künstlerische Disziplin und vermag dabei die undankbare Reputation als bloße Handwerkslehre abzuschütteln. Hinsichtlich des Anspruches auf Wissenschaftlichkeit dominiert in dieser Strömung zunächst eine historisch-positivistische Grundhaltung, die auf ein Verständnis historisch verorteter musikalischer Gegebenheiten im Kontext der jeweils überlieferten Kompositionen und theoretischen Schriften abzielt. In der Kombination mit der künstlerischen Ausrichtung entsteht so eine neue Form lebendiger Bewahrung der Traditionsbestände, die das ästhetische Urteil in die Bewertung überlieferter Auffassungen einbezieht. Spätestens seit der Gründung der Gesellschaft für Musiktheorie im Jahre 2000 beginnt sich dieses Selbstverständnis in Richtung einer Auffassung von Musiktheorie zu erweitern, die neben ihren künstlerischen und pädagogischen Zielen darum bemüht ist, ihrem Anspruch auf Wissenschaftlichkeit durch eine Balance von historisch und systematisch ausgerichteten Ansätzen gerecht zu werden. Stefan Rohringers Glosse aus dem Jahr 2006 zur veränderten Namensgebung der Zeitschrift Musiktheorie[9] bietet einen Einblick in die Dynamik dieses Prozesses und legt insbesondere eine neuerliche Beschäftigung mit dem musiktheoretischen Denken und Argumentieren von Carl Dahlhaus nahe.

2. Im Jahre 1979 findet in La Jolla (Kalifornien) die erste internationale Tagung der damals neu gegründeten Cognitive Science Society statt und institutionalisiert damit die interdisziplinären Bemühungen zwischen Psychologie, Neurowissenschaft, Informatik/Künstlicher Intelligenz, Linguistik, Philosophie und Anthropologie um eine gemeinsame Erforschung der diversen Leistungen und Fähigkeiten des menschlichen Geistes mittels Theoriebildung, Modellierung und Empirie.[10] Markus Pearce und Martin Rohrmeier erinnern an die Rolle der Musik in der Kognitionsforschung und die einschlägigen Arbeiten von Christopher Loguet-Higgins, Mark Steedman, Carol Krumhansl, Diana Deutsch und anderen Autoren, die substanziell zur Erschließung dieses Gegenstandsbereiches beigetragen haben.[11] Die vielbeachtete und vor allem seitens der Musiktheorie kritisch rezipierte Generative Theory of Tonal Music von Ray Jackendoff und Fred Lerdahl kann als ein Meilenstein innerhalb dieser Strömung gelten. Dort wird der Gegenstandsbereich der Musiktheorie in der Kognition verortet:

Where, then, do the constructs and relationships described by music theory reside? The present study will justify the view that a piece of music is a mentally constructed entity, of which scores and performances are partial representations by which the piece is transmitted. One commonly speaks of musical structure for which there is no direct correlate in the score or in the sound waves produced in performance. One speaks of music as segmented into units of all sizes, of patterns of strong and weak beats, of thematic relationships, of pitches as ornamental or structural important, of tension and repose, and so forth. Insofar as one wishes to ascribe some sort of ›reality‹ to these kinds of structure, one must ultimately treat them as mental products imposed on or inferred from the physical signal. In our view, the central task of music theory should be to explicate this mentally produced organization. Seen in this way, music theory takes place among traditional areas of cognitive psychology such as theories of vision and language.[12]

3. In den 1970er und 80er Jahren erscheinen mehrere Beiträge und programmatische Entwürfe, unter anderem von John Clough[13], John Clough und Gerald Myerson[14], David Lewin[15], Guerino Mazzola[16], Eric Regener[17] und Rudolf Wille[18], die auf die Einführung von neuen mathematischen Untersuchungsmethoden in den Gegenstandsbereich der traditionellen Musiktheorie abzielen. Der zunächst langsam einsetzende Diskurs über die mathematische Musiktheorie erfährt inzwischen eine Institutionalisierung auf internationaler Ebene durch die Tagungen und Publikationstätigkeit der 2007 gegründeten Society of Mathematics and Computation in Music. Die Mathematiker Mazzola und Wille betonen in ihren Ansätzen jeweils die wichtige Rolle der Mathematik als Metasprache und besinnen sich dabei auf deren Status als Geisteswissenschaft. Damit treten sie einem verbreiteten Missverständnis entgegen, aufgrund dessen gerne auch die Neuanfänge unter den Generalverdacht der ontologischen Kontemplation gestellt werden.[19] Dieses Missverständnis beruht letztlich auf dem immensen Erfolg der angewandten Mathematik in der Physik und auf einer unreflektierten Vermischung eines epistemologisch begründeten mathematischen Natürlichkeitsbegriffs[20] mit der ontologisch begründeten Auffassung von der Physik als einer Naturwissenschaft. Die wohl am engsten mit dem Gegenstandsbereich der alten Theorie verbundene Untersuchungsrichtung innerhalb der neueren mathematischen Musiktheorie beschäftigt sich mit den Begriffen der Diatonizität. Mit wenigen Ausnahmen äußern sich die darin involvierten Autoren, wie John Clough, Jack Douthett, Norman Carey, David Clampitt in Hinblick auf ontologische Fragen eher zurückhaltend. Zu den Ausnahmen gehört Eytan Agmon, der auf eine kognitive und kommunikative Interpretation seiner Ergebnisse abzielt. Die eigenen Untersuchungen des Autors auf diesem Gebiet verfolgen das Ziel, latente Verbindungen zwischen der alten und neuen Theorie bzw. innerhalb verschiedener Zweige der alten Theorie aufzudecken und mit mathematischen Mitteln zu fassen.

Wenn nun in der gegenwärtigen Situation die Aufgabe einer verstärkten Integration der jeweils innerhalb der drei genannten Strömungen erzielten Errungenschaften im Raum steht, so ist die Frage nach der Ausrichtung systematischer Musiktheorie wieder hochaktuell. Erwähnenswert ist eine Kontroverse, die in einem Diskurs von aktiven Verfechtern mathematischer Untersuchungen zu musiktheoretischen Fragen ausgetragen wird.[21] Neben Mathematisierungsansätzen innerhalb der Musiktheorie finden mathematische Ansätze auch innerhalb der Kognitionswissenschaften Eingang in die Musikforschung. Obgleich die Mathematik als gemeinsame Sprache potenziell dabei helfen kann, Verbindungen zu schaffen zwischen der logischen Analyse abstrakter musiktheoretischer Begriffe einerseits und dem Modellieren verkörperter Kognition andererseits, erfordert die Perspektive einer solchen Integration eine gegenseitige Standortbestimmung, die mit der allgemeineren Frage nach dem Selbstverständnis und dem Gegenstandbereich der Musiktheorie eng zusammenhängt.

Der Kognitionsforscher Geraint Wiggins verortet die Gegenstände der Musiktheorie im Bereich der Kognition, wie schon Lerdahl und Jackendoff, und sieht es folgerichtig als angemessen an, wenn sich die Mathematik der Modellierung musikalischer Kognition widmet. Allerdings geht er in seiner Stellungnahme noch einen Schritt weiter, indem er die Mathematisierung abstrakter musiktheoretischer Gegenstände als irreführend bezeichnet, was wiederum an Dahlhaus’ Missbilligung der »›ontologischen‹ Kontemplation« erinnert:

I propose that mathematical modelling of certain kinds may be appropriate to model certain musical relationships, but this is so because of underlying cognitive principles. The conclusion is that to model music mathematically is essentially to model (parts of) cognition mathematically, which means that to model music in the abstract, as though it were itself a mathematical construct, divorced from its source in the human mind, is misleading. For a true understanding, the power of mathematics should be applied to the process of musical behaviour, not merely to its product. That process lies in the embodied human mind.[22]

Soweit sind Wiggins’ Zweifel an der Zweckmäßigkeit mathematischer Modellierung abstrakter musiktheoretischer Gegenstände pragmatischer Natur und scheinen zunächst nur auf der Annahme zu beruhen, dass eine angemessene ontologische Verortung der Gegenstände eine notwendige Bedingung zu wirklicher wissenschaftlicher Erkenntnis bildet. Diese implizite Annahme ist jedoch entscheidend für die gesamte Diskussion. Selbst wenn ontologische Klarheit für das Erzielen von Erkenntnissen tatsächlich notwendig wäre, dann – so lehrt die Geschichte der Mathematisierungsversuche von Geistestätigkeit – muss sie keine hinreichende Bedingung für einen zeitnahen wissenschaftlichen Durchbruch darstellen.

Bereits Johann Friedrich Herbart verkündet in durchaus vergleichbarer Weise den wissenschaftlichen Anspruch hinter seinem mathematischen Ansatz zur Vorstellungsmechanik, deren Erklärungskraft er am Beispiel der Tonlehre nachzuweisen glaubt:

Die Psychologie hat in demjenigen Gebiete, worin wir uns hier versetzen, nicht eigentlich zu lernen, sondern sie lehrt, in Folge der Prinzipien, die sie schon besitzt; und ihre Lehre geht ohne allen Vergleich weiter, als bloss auf die Tonkunst, die vielmehr ein sehr untergeordneter Gegenstand für die Lehre im Ganzen genommen ist. Allein, indem sie lehrt, – indem sie Constructionen a priori entwirft, – entsteht der uns wohl bekannte Zweifel, ob die Lehre nicht etwa ein Hirngespinst sey, wie es viele giebt. Darum bedarf die Lehre einer Bestätigung; und hierzu werden in der Erfahrung veste Puncte gesucht, mit denen die Lehre zusammentreffen soll. Denn eben diese sind das, was sie erklären soll. Könnte man solcher festen Puncte viele finden, so hätte die Tonlehre keinen besonderen Vorzug. Allein während es der Bestätigungen viele und mancherley gibt, sind sie doch nicht alle von gleichem Werthe, weil in vielen Fällen die Lehren der Psychologie bestimmter lauten, als dasjenige sich beobachten lässt, was in der Erfahrung mit ihr zusammentreffen soll; indem es vielmehr so schwankend, zerfliessend, vieldeutig ist, dass für eine Vergleichung keine sichern Resultate gewonnen werden.[23]

Ob nun Herbarts Beitrag zur Psychologie obsolet bleibt oder noch seiner Aufarbeitung harrt, mag dahingestellt sein. Jedenfalls ist es bei der Verortung systematischer Musiktheorie nicht ratsam, ausschließlich einer teleologischen Überzeugung zu folgen, der zufolge die Ausrichtung auf die kognitive Realität letztendlich zu einem Durchbruch in der Erforschung von Musik führen muss.

Sonderbar verführerisch erscheint gerade deshalb ein zweiter Argumentationsstrang in Wiggins’ Stellungnahme, in welchem er seine epistemologischen Einwände gegen die Mathematisierung abstrakter musikalischer Begriffe aus einer psychologischen Theorie des alltäglichen Theoretisierens bezieht. Traditionelle Musiktheorie, vor allem solche die versucht, musikalische Praxis mithilfe von Regeln einzufangen, charakterisiert er als eine Instanz der sogenannten ›Theory-Theory‹, welche in der Psychologie auch als ›Folk Psychology‹ bezeichnet wird. Danach helfen die traditionellen musiktheoretischen Ansätze Musikern, sich mehr oder weniger erfolgreich in ihrem Tätigkeitsfeld zu orientieren und sich gegenseitig darüber auszutauschen. Wissenschaftliche Erkenntnis kann Wiggins zufolge auf diesem Wege jedoch nicht erzielt werden, ungeachtet der beträchtlichen akademischen Institutionalisierung der Musiktheorie. Seinen Diskussionspartnern Alan Marsden und Guerino Mazzola, die auch andere Formen der musiktheoretischen Erkenntnis in Betracht ziehen, versucht er nachzuweisen, dass sie dabei entweder implizit kognitives Terrain betreten, oder dass die aufgeführten Ergebnisse nicht den Erfüllungsbedingungen genügen, welche an letztere angelegt werden. Sein Fazit lautet:

I restate and amplify my argument that music theory should embrace its status as a folk psychology, and appeal to psychology as an encompassing framework within which musical phenomena which are not explicable by reference only to the musical surface may be engaged. This position opens up a new range of possibilities for the application of mathematics and computation in the study of music.[24]

Ungeachtet der zugespitzten Formulierungen scheint sich Wiggins’ Argumentation auf den ersten Blick mit derjenigen von Dahlhaus zu decken. Es geht darum, die Verquickung der Theorie mit der Handwerkslehre aufzulösen und perspektivisch die gestaltenden Prinzipien im musikalischen Bewusstsein zu erforschen – im Sinne einer Verwirklichung des von Riemann angedachten Projekts einer »Lehre von den Tonvorstellungen«. Es ist allerdings erstens fraglich, ob Dahlhaus dabei an eine Auflösung der systematischen Musiktheorie in den Kognitionswissenschaften gedacht hat, und zweitens dürfte diese Sichtweise auch dem wissenschaftlichen Selbstverständnis der GMTH zuwider laufen.

Plädiert wird hier indes für einen transdisziplinären Ansatz, in welchen sich die Musiktheorie bereits als wissenschaftliche Disziplin mit einem eigenen Gegenstandsbereich einbringt, der auch ihre Traditionsbestände angemessen berücksichtigt. Ein Prinzip der ontologischen Klarheit sollte zweifellos jedes wissenschaftliche Arbeiten leiten. Bei einem so schwierig zu erschließenden Gegenstandsbereich wie dem der menschlichen Geistestätigkeit ist es jedoch vernünftig, neben mehr oder weniger direkten auch nach indirekten Zugängen zu suchen, bei denen die wissenschaftliche Untersuchung von Hilfsgegenständen möglicherweise entscheidende Einsichten liefern kann für das Verständnis des primär interessierenden Gegenstandsbereichs. Die Erhebung solcher Hilfsgegenstände zum Forschungsthema ist eine reine Frage der Zweckmäßigkeit, nicht aber der Wissenschaftlichkeit an sich. Insbesondere betrifft dies eben auch die Beschäftigung mit überlieferten musiktheoretischen Ideen auf der Grundlage von mathematischen Untersuchungen an abstrakten Begriffen.

Der im Titel »Die Vernunft in der Tradition« zum Ausdruck gebrachte Leitgedanke, der hinter den Überlegungen des vorliegenden Beitrages steht, zieht ganz konkret die Möglichkeit in Betracht, dass das überlieferte musiktheoretische Wissen trotz aller Hindernisse, die sich einer Anerkennung der historischen Quellen als wissenschaftliche Beiträge im heutigen Sinne entgegenstellen, eine wertvolle Erkenntnisquelle für mathematische Untersuchungen auf einer abstrakten begrifflichen Ebene darstellen kann. Der bewusste Verzicht auf ontologische Deutungen macht die mathematische Begriffsanalyse handhabbar und lässt zugleich den Vorwurf der ontologischen Kontemplation ins Leere laufen.

Hierbei darf also einerseits der besondere Stellenwert, der dem Denken in abstrakten Begriffen innerhalb der Musiktheorie beigemessen wird, nicht bereits mit ontologischer Fokussiertheit verwechselt werden. Andererseits soll natürlich die Perspektive einer transdisziplinären Forschung genau bei der Möglichkeit einer kognitiven Ausdeutung solcherart gewonnener musiktheoretischer Erkenntnisse ansetzen. In diesem Zusammenhang kann deshalb nicht verschwiegen werden, dass Helga de la Motte-Haber und Peter Nitsche den Vorwurf der ontologischen Kontemplation nicht nur gegen waschechte Platonisten richten, sondern auch gegen die Protagonisten psychologisch motivierter Ansätze, wie Hugo Riemann, Ernst Kurth und auch Jacques Handschin, in denen der Frage nach dem Wesen des Musikalischen ein höherer Rang einräumt wird, als den ästhetischen Fragen, die auf die Deutung des einzelnen Kunstwerks zielen. In einer Bilanz lassen beide eine gewisse Ambivalenz hinsichtlich der Konsequenzen ihrer Kritik für die Musikwissenschaft erkennen:[25]

Die Herausforderung dieser Theorien wurde in der Musikwissenschaft nicht recht begriffen, daher verkümmerte die Theorie der Musik zu einem Drehen und Wenden von einzelnen satztechnischen Sachverhalten. Es kam sogar so weit, daß der Gedanke, es bedürfe für die Musikwissenschaft einer Theorie, damit sie sich als Fach mit einem definierten Gegenstand vorstellen könne, fast den Spekulationen über die Theorie der Theorien nachgeordnet wurde.[26]

De la Motte-Haber und Nitsche stellen sich der Herausforderung jener Theorien mit dem Verweis auf die Frage, »ob es zeitlose Beziehungen gibt, auf denen die Aktivitäten des erkennenden und erlebenden Subjekts beruhen könnten«.[27] Damit fällt allerdings deren Aufarbeitung in den Zuständigkeitsbereich der Kognitionswissenschaften, und der Musiktheorie bliebe unter diesem Blickwinkel nur die Aufgabe der ästhetischen Deutung des einzelnen Kunstwerks.

Im Zuge der Aufbruchsbewegung der GMTH gilt es deshalb, die Frage nach der Herausforderung jener Theorien auch für die Musiktheorie neu zu stellen. Zur Rezeptionsgeschichte des ›Toncharakters‹ gehört auch ein Diskussionsstrang um die Perspektiven systematischer Musiktheorie in der Musikwissenschaft. In der eingangs zitierten Stellungnahme zur Musiktheorie als Traditionsbestand der Systematischen Musikwissenschaft spielt Dahlhaus nicht zufällig auf Handschins Unterscheidung zwischen ›Theoretikern‹ und ›Theorielehrern‹ an, denn sie zielt letztlich auch auf Handschins eigenes Selbstverständnis als Theoretiker bzw. Wissenschaftler, dem es darum geht, eine Brücke zu schlagen von der älteren Theorie, welcher er als Historiker eine hohe Wertschätzung entgegenbringt, hin zu seinen eigenen theoretischen Ambitionen.

Den Hintergrund für jene nur angedeutete Bezugnahme auf Handschin durch Dahlhaus bildet wohl Walther Wioras ausführlicher Review-Artikel[28] zum Toncharakter. Dort findet beispielweise auch der Terminus der ›ästhetischen Kontemplation‹ Verwendung, um die Eigenständigkeit des musikalischen Tons gegenüber seinen Schalleigenschaften zu charakterisieren. Unter der Überschrift »Dogmatische und systematische Musiktheorie« würdigt Wiora in Handschin den Begründer einer ›systematischen Musiktheorie‹:

Am Schluß des Buches stellt H[andschin] das musiktheoretische Denken dem ›musiktheoretischen‹ gegenüber. Durch Anführungsstriche bezeichnet er hier gerade das stilgebunden technische Wissen als theoretisch im uneigentlichen Sinne. Nun hat sich in etlichen Geisteswissenschaften die Unterscheidung zwischen dogmatischen und systematischen (neben historischen) Zweigen eingeführt […]. In diesem Sinne trennen wir einen systematischen Zweig der Musiktheorie von dogmatischen Zweigen und verstehen H[andschin]s Leistung als einen wesentlichen Beitrag zu seiner Grundlegung. Darin geht er über Riemann hinaus, der auf seinen Wegen zur reinen Theorie viel mehr in dogmatischen Denkweisen befangen blieb.[29]

Diese Würdigung ist aus verschiedenen Gründen problematisch. Ohne Handschins Intentionen vollauf gerecht zu werden, drängt sich Wioras Review wohlmeinend vor das rezensierte Buch und muss dafür später auch als dessen Blitzableiter herhalten.[30] Sein Plädoyer zugunsten einer systematischen Musiktheorie erzeugt indes wenig positiven Nachhall in der systematischen Musikwissenschaft.[31] Am ehesten zeigen sich in der Art und Weise von Dahlhaus’ inhaltlicher Auseinandersetzung mit Handschins Ansatz in den Untersuchungen mögliche Spuren von Wioras Einfluss.[32]

Handschin nimmt die Kollision seines tonpsychologischen Ansatzes mit dem damaligen Selbstverständnis der Musikpsychologie als Wissenschaft aus inhaltlichen Erwägungen ganz bewusst in Kauf. Angesichts der engen Verzahnung von historischen, systematischen und psychologischen Argumenten im Toncharakter könnte man aus heutiger Perspektive in Handschin eher den Wegbereiter einer noch ausstehenden Integration von historischer und systematischer Musiktheorie und der Kognitionsforschung sehen. Die Ausarbeitung einer entsprechenden Agenda ist Gegenstand einer gesonderten Abhandlung.[33]

Aufschlussreich für sein Urteil über Musiktheorie als Handwerkslehre und seine Vision von transdisziplinärer Musikforschung ist dabei auch eine frühe Stellungnahme, die der Orgelvirtuose[34] Handschin im Petrograd des Jahres 1919 als frisch ernannter Leiter der Wissenschaftlich-theoretischen Sektion der akademischen Unterabteilung der Musikabteilung Muzo des Volkskommissariats für Bildung mit Fragen der Forschungsorganisation anlässlich des Aufbaus eines akustischen Laboratoriums[35] in einem programmatischen Text festhält:

Uns erstaunt zuvorderst, dass die sogenannte Theorie der Musik, wissenschaftlich gesprochen, keine Theorie ist, sondern nur eine mehr oder minder systematische Darlegung einer Reihe praktischer Ratschläge, die von der Autorität des einen oder anderen Meisters der musikalischen Praxis bekräftigt wurde. Auf dem Gebiet der Harmonik studiert der eine Schüler nach Reger, der andere nach Rimsky-Korsakow, wobei beide zuweilen das völlige Gegenteil behaupten und weder der eine noch der andere in der Lage zu beweisen ist, dass der eine Recht hat und der andere nicht. […] Die Musik ist eine Kunst, die auf unmittelbare Wahrnehmung abzielt, und deshalb muss in der Wissenschaft der Musik all das einen sehr hohen Stellenwert erlangen, was wir über die Psychologie der Wahrnehmung wissen. […] Mit Hilfe dieser drei Disziplinen muss die Musik neue Kräfte schöpfen: der Physik, der Physiologie und der Psychologie.[36]

Es kann im Zuge einer Aufarbeitung weder darum gehen, Handschins Untersuchungen zum Toncharakter auf einen Ontologie-freien theoretischen Ansatz zurechtzustutzen, noch darum, den Gegenstandsbereich der systematischen Musiktheorie zu überdehnen, um jene Aufarbeitung dann doch innerhalb ihrer Grenzen bewerkstelligen zu können. Wohl aber kann die Identifikation einer Leitidee hinter dem Begriff des ›Toncharakters‹ den Ausgangspunkt für eine eigenständige theoretische Untersuchung bilden, die sich im zweiten Schritt an Handschins Wertschätzung der Vernunft in der Tradition orientiert und sich um eine Integration neuer und alter Wissensbestandteile bemüht, und die dann in einem dritten Schritt zusammen mit anderen Beiträgen[37] in ein transdisziplinäres Projekt einer umfassenderen Aufarbeitung münden kann. Die in den folgenden Abschnitten vorgestellten Untersuchungsergebnisse zur Diatonizität können innerhalb der Musiktheorie diskutiert und bewertet werden, und können deshalb den ersten beiden Stufen des ansonsten hier nur skizzierten dreistufigen Plans zugeordnet werden.

Einen Orientierungspunkt dazu bietet die Positionierung von Carl Dahlhaus zur Frage der Begründung von harmonischer Tonalität im ersten Kapitel der Untersuchungen, zu der ihn nicht zuletzt seine Auseinandersetzung mit Handschin veranlasst.[38] Einerseits erkennt er die Aktualität und Problematik der ontologischen Fragestellungen an:

Nichts wäre falscher, als in den Gegensätzen zwischen Fétis und Riemann – zwischen ›natürlicher‹ und ›geschichtlich-ethnischer‹ Begründung, zwischen der Deduktion tonaler Zusammenhänge aus ›Tonverwandtschaften‹ und der Berufung auf die Antithese von ›tendance‹ und ›repos‹, zwischen dem Anspruch auf umfassende und der Beschränkung auf eine begrenzte Geltung der Theorie – ein Stück tote Vergangenheit zu sehen. Es ist immer noch problematisch, ob eine ›natürliche‹ Begründung der harmonischen Tonalität möglich ist […].[39]

Andererseits vertraut Dahlhaus im Wesentlichen auf die Integration von historischem und systematischem musiktheoretischen Denken und klammert das Projekt einer Beantwortung jener ontologischen Fragen aus seinen Untersuchungen aus:

Ob oder in welchem Maße die harmonische Tonalität in der Natur der Musik oder des Menschen begründet ist, muß offen gelassen werden. Das Thema der Untersuchung, die Entstehung der harmonischen Tonalität in der Mehrstimmigkeit des 16. und 17. Jahrhunderts, kann behandelt werden, ohne daß entschieden werden müßte, ob die ›Entstehung‹ als ausschließlich geschichtlicher Vorgang oder als Ausprägung eines von Natur vorgezeichneten Sachverhalts zu deuten ist.[40]

Dass der Systematik in solch einem Projekt eine zentrale Rolle zuwächst, bringt Thomas Christensen in seinem Review der amerikanischen Übersetzung der Untersuchungen folgendermaßen treffend auf den Punkt:

In order to write a history of tonality, the potential historian must as a prerequisite decide upon a definition of tonality. How else is there to write its history?[41]

Dahlhaus stellt sich dieser Herausforderung durchaus[42] und exemplifiziert dabei eine argumentative Herangehensweise an systematische Fragen, die es mit mathematischen Mitteln zu verfeinern und zu erweitern gilt.

2. In der ›dünnen Luft der Abstraktionen‹: Formale Begriffsanalyse der Diatonizität

Im Kern dreht sich Handschins Abhandlung zum Toncharakter um die Idee eines zweifachen Gegebenseins musikalischer Tonbeziehungen auf der Grundlage der Zugehörigkeit der Töne zu einem Tonsystem:

Die Wirklichkeit des Tons beruht vielmehr darauf, daß er Glied eines Systems ist […]. Das was wir in den Toncharakteren vor uns haben, ist die eigentliche musikalische Qualität des Tons; und es ist ›etwas Wunderbares‹, daß diese Qualität offenbar nur durch die Zugehörigkeit des Tons zum System zustande kommt. Oder sagen wir besser: sie besteht darin.[43]

Konkret manifestiert sich das Gegebensein der Tonbeziehungen nach Handschins Auffassung in zwei einander durchkreuzenden Ordnungen: einer ›äußeren‹ nach Tonhöhen und einer ›inneren‹ nach Quintabständen. Musikalisch manifestiert sich jene innere Ordnung als eine Skala von Tonqualitäten, die Handschin ›Toncharaktere‹[44] nennt:

Wenn ich diese ›Charaktere‹ als die eigentlich musikalische Eigenschaft des Tons ansehe, möchte ich damit die Rolle der Tonhöhe und der Tonhöhenunterschiede nicht herabsetzen. Die volle Mannigfaltigkeit der Musik als Melodie beruht auf dem Spiel dieser beiden Kategorien, die sich ständig durchkreuzen; und der im vollen Sinn ›Musikalische‹ ist derjenige, der sowohl auf die inneren Tonbeziehungen eingestellt ist, als auch die Höhenabstufungen im Verhältnis zu jenen wahrnimmt.[45]

Die Betonung jener zweiten Dimension neben der Tonhöhe transportiert Handschins zentrale Botschaft an die Adresse der Psychologie. In seiner Auseinandersetzung mit der Tonpsychologie Carl Stumpfs kritisiert Handschin deren einseitige Fokussierung auf den Tonhöhenparameter. Seiner Meinung nach übersieht die tonpsychologische Forschung damit einen für das Verständnis musikalischer Wahrnehmung wesentlichen Bereich.

Vor dem Hintergrund des bereits Gesagten besteht das Besondere und für manchen Leser wohl Irritierende an Handschins These in der Radikalität, mit der die Quintordnung der Töne zum Zünglein an der Waage zwischen ästhetischer und ontologischer Kontemplation wird. Niemand wird bestreiten, dass ein jeweiliger musikalischer Kontext die Bedeutungen der darin wahrgenommenen Töne beeinflusst. Der entscheidende Punkt besteht in der Rolle des Tonsystems, welchem im Zuge dieser musikalischen Bedeutungskonstitution eine wie auch immer geartete Realität in der musikalischen Mentalität zugemutet wird. Man wird Handschins Intentionen nicht gerecht, wenn man diesen zentralen Punkt seines Ansatzes verwässert.[46] Vielmehr muss jene Leitidee in Form einer überprüfbaren Hypothese zur Musikkognition reformuliert werden. Die Rolle der Musiktheorie kann unterdessen darin bestehen, auf der Basis von Untersuchungen zu den theoretischen Konsequenzen dieser Leitidee derselben Relevanz zuzusprechen oder abzusprechen.

Worin aber besteht der mathematische Kern von Handschins Leitidee? In Begleitung eines Einwandes gegen eine bestimmte inhaltliche Deutung des Toncharakters lässt Dahlhaus die Bemerkung fallen, dass nur die formale Definition des Toncharakters als nach ›innen gewendete‹ Position im System unwiderlegbar sei.[47] Der hinter dieser Formulierung lauernde Spott gründet auf der Unterstellung, dass über die tautologische Gleichsetzung von Definiens und Definiendum hinaus nichts Unwiderlegbares zum Toncharakter gesagt werden könne.

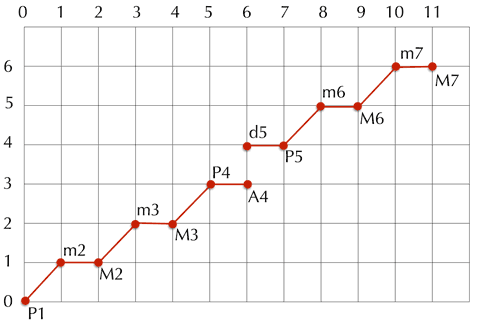
Wie nun dargelegt wird, kann indes ein großer Teil von Erkenntnissen der Diatonic Set Theory retrospektiv als ein gesichertes Wissen über den Toncharakter gedeutet werden. Zum Einstieg mag eine Beobachtung Handschins dienen, wonach sich die verschiedenen Charaktere der diatonischen Intervalle in der Verschiedenheit der jeweiligen Vielfachheiten ihres Auftretens innerhalb des diatonischen Systems niederschlagen:

Gehen wir nun zu den weiteren Intervallen über: wir sehen, dass der großen Sekunde, die zwei Quintschritte, also einen größeren Charakterunterschied als die Quinte repräsentiert, nur noch fünf ›Verwirklichungen‹ entsprechen, der großen Sext und kleinen Terz vier, der großen Terz und kleinen Sext drei, der kleinen Sekund zwei, und dem Tritonus und seiner Umkehrung nur eine.[48]

Um diese Eigenschaft eines lückenlos gestaffelten Intervallgehaltes noch besser zu verstehen, ist es nützlich, diese vor dem Hintergrund anderer generierter bzw. sogar willkürlich gebildeter Skalen zu untersuchen. Die dabei vorzunehmende Mathematisierung des Skalenbegriffs ist allerdings nicht durch ein vordergründiges Bedürfnis nach Exaktheit motiviert, welche vielmehr eine Grundvoraussetzung für die Mathematisierung ist; sondern im Kern der Sache geht es um den Akt der Verallgemeinerung aus einem Erkenntnisinteresse heraus. Dabei werden bestimmte Eigenschaften eines betrachteten Gegenstandes als essenziell und andere als akzidenziell angesehen. Erstere erscheinen im Fokus der Definition und der darauf aufbauenden Untersuchungen. Mit der Entscheidung, eine oder mehrere Eigenschaften als essenziell anzusehen, verlässt der Theoretiker neutralen Boden und strebt danach, weitere logische Konsequenzen dieser Entscheidungen mit musiktheoretischen Aussagen zu interpretieren.

Wenn man sich also fragt, ob und wie die beiden Eigenschaften der Generiertheit und des lückenlos gestaffelten Intervallgehaltes logisch voneinander abhängen, muss man sich zunächst bewusst machen, dass in einer willkürlich aus n Tonhöhen gebildeten Skala – abgesehen von den n Primen – jedes der n(n-1) gerichteten Intervalle eine eigene unverwechselbare spezifische Größe haben kann. Bei einem lückenlos gestaffelten Intervallgehalt hingegen verteilen sich diese n(n-1) Intervalle auf genau 2(n-1) spezifische Größen, deren Vielfachheiten zweimal von 1 bis n-1 gestaffelt sind. So verteilen sich die 42 Intervalle der Quint-generierten diatonischen Skala auf lediglich 12 spezifische Größen. Davon entfallen 6 auf die ›primären‹ Intervalle, die man entlang der Quintenkette in Kreuz-Richtung bilden kann, nämlich die Quinte (P5), die große Sekunde (M2), die große Sexte (M6), die große Terz (M3), die große Septime (M7) und die übermäßige Quarte (A6). Die anderen 6 Größen entfallen auf die entsprechenden ›sekundären‹ Umkehrintervalle, die man entlang der Quintenkette in Be-Richtung bilden kann, nämlich die Quarte (P4), die kleine Septime (m7), die kleine Terz (m3), die kleine Sexte (m6), die kleine Sekunde (m2) und die verminderte Quinte (d5). Die Vielfachheit einer spezifischen Intervallgröße ergibt sich als die Differenz aus 7 und der betreffenden Quintenbreite.

Diese Argumentation kann man unschwer übertragen auf eine beliebige (oktav-periodische) Skala, die als Intervallkette mit einer einzigen spezifischen Intervallgröße generiert werden kann, ohne zugleich völlig regulär zu sein. Dazu darf die Größe des Restintervalls zwischen dem letzten und dem ersten Ton der Generierungskette nicht mit derjenigen der normalen Kettenglieder übereinstimmen.[49] Damit ist zunächst klar: Nicht reguläre Generiertheit impliziert einen lückenlos gestaffelten Intervallgehalt. Sind die beiden Eigenschaften sogar äquivalent?

Eine musikalisch relevante Konsequenz eines lückenlos gestaffelten Intervallgehalts ist, dass die Transpositionen einer solchen Skala einander in stufenweise variierenden Graden überschneiden. Für generierte Skalen leuchtet dies sofort ein, denn wenn einige Kettenglieder von einem Ende der Kette entfernt und am anderen wieder angefügt werden, überschneiden sich Ausgangsskala und Transposition exakt im unveränderten Teil der Kette. Eine einfache Überlegung zeigt jedoch, dass eigentlich auch ein lückenlos gestaffelter Intervallgehalt genügt, um diesen Effekt zu erzielen. Die Ketteneigenschaft ist dazu nicht zwingend erforderlich. Gibt es eine nicht-generierte Skala mit lückenlos gestaffeltem Intervallgehalt?

Der bequemste Weg zu einer Antwort führt über ein musikalisches Beispiel. Für ein Verständnis der Rolle des ›Farbenakkords‹ C-G♯-B-E-A in Arnold Schönbergs Orchesterstück op. 16/3 ist nämlich die Feststellung aufschlussreich, dass sich der Akkord und seine Großterztransposition in den drei Tönen des übermäßigen Dreiklangs C-E-G♯ überschneiden.[50] Damit kommt dieser Akkord dem gesuchten Beispiel schon nahe genug, um es zu finden: Der 4-tönige Ganztonakkord C-D-E-G♯ in ›temperierter‹ Auffassung ist nicht generiert, besteht aber aus drei großen Terzen, zwei Ganztönen und einem Tritonus. Kurioserweise handelt es sich dabei um die einzige Manifestation einer nicht-generierten Skala mit lückenlos gestaffeltem Intervallgehalt überhaupt. Sie erbringt dennoch unzweifelhaft den Nachweis, dass die Eigenschaft eines lückenlos gestaffelten Intervallgehalts die Eigenschaft der Generiertheit nicht impliziert.

Auf extensionaler Seite bringt das Geschäft des Verallgemeinerns mit sich, dass die Begriffsumfänge unzählige – musikalisch gesehen – kontrafaktische Gegenstände beinhalten. Um die Eigenschaften der diatonischen Skala besser zu verstehen, gehen einige Autoren im Rahmen der Diatonic Set Theory der Frage nach, welche Teilmengen des 12-Tonsystems – oder sogar beliebiger n-Tonsysteme variierender Kardinalität n – diese Eigenschaften teilen. Dies mag wiederum die Assoziation befördern, es gehe vordergründig um eine Suche nach exotischen Skalen, Klängen etc. Diese Sicht beleuchtet zwar einen mitunter willkommenen Teilaspekt, verstellt aber auch den Kern der Sache. Erst im Akt der Verallgemeinerung mehrerer Eigenschaften eines Gegenstandes zeigen sich deren logische Abhängigkeiten untereinander.

So paradox es scheinen mag, führt ausgerechnet eine kompositorisch motivierte kombinatorische Untersuchung von Teilmengen des Zwölfhalbtonsystems (›pitch class sets‹) unter einem atonalen Paradigma zu einem erneuerten theoretischen Interesse an der Diatonik.[51] Die Präsupposition des Zwölfhalbtonsystems als Beschreibungsrahmen führt indes dazu, dass die von Handschin beobachtete Eigenschaft nun in abgewandelter Form definiert wird. Eine ›pitch class set‹ besitzt die sogenannte ›deep scale property‹, wenn jede chromatische Intervallklasse darin in einer ihr eigenen Vielfachheit auftritt. Diese Eigenschaft eines lückenlos gestaffelten chromatisch vollständigen Intervallgehalts wird nicht von jeder generierten ›pitch class set‹ erfüllt. Zum Beispiel ist die pentatonische ›pitch class set‹ {0, 2, 5, 7, 9} zwar Quint-generiert, schöpft aber das chromatische Intervallsystem nicht aus. Sie enthält weder eine Instanz der Intervallklasse 1, noch eine der Intervallklasse 6 und beide Intervallklassen treten folglich mit derselben Vielfachheit 0 auf.

Die Präsupposition eines chromatischen Beschreibungsrahmens bei der ›atonalen‹ Re-Konzeptualisierung von Diatonizität weckt im Zusammenhang mit deren traditionellen Bestimmungen auch jenes teilweise berechtigte Misstrauen gegenüber vorgreifenden Anachronismen. Allerdings sollten diese in systematischen Ansätzen keineswegs tabuisiert werden. Gerade die Beobachtung, dass die Ansätze der Diatonic Set Theory nicht nur zu ›aufgesetzten‹ Begriffen führen, ist geradezu der Anlass für das hier verfolgte Integrationsprojekt zwischen neuer und alter Theorie der Diatonizität. Am Beispiel der ›deep scale property‹ zeigt sich in besonderer Weise, dass ein umsichtiges Vorgehen geboten ist.[52]

John Clough überträgt die Methoden der Akkordklassifikation von der Atonal Set Theory vom zwölfstufigen chromatischen Tonsystem auf die siebenstufige Diatonik.[53] Wenn auch der Neuheitsstatus für diese Klassifikation eigentlich dem sieben Jahre früher erschienen Büchlein von Franz Alfons Wolpert gebührt[54], so kann der genannte Artikel als einer der Auslöser für eine ganze Untersuchungsrichtung gelten, die in der amerikanischen Literatur bislang mit dem Namen Diatonic Set Theory belegt wird.

Neben der ›deep scale property‹ werden eine Reihe weiterer besonderer Eigenschaften der Diatonik zutage gefördert. Einen Durchbruch zu neuen Ideen und Erkenntnissen erbringt die Zusammenarbeit von John Clough mit dem Mathematiker Gerald Myerson.[55] Anhand einer Überlagerung der ›generischen‹ siebentönigen Beschreibungsebene mit der ›spezifischen‹ zwölftönigen untersuchen die beiden Autoren die Kombinatorik von Intervallen, Akkorden und Tonfolgen. Als ›Myhill-property‹[56] bezeichnen sie beispielsweise die Eigenschaft, dass jedes generische Intervall mit Ausnahme von Prime (bzw. Oktave) in genau zwei spezifischen Größen auftritt: die generische Sekunde als kleine bzw. große Sekunde, die generische Terz als kleine bzw. große Terz, die generische Quarte als reine bzw. übermäßige Quarte etc. Die Differenz zwischen den beiden Species ist in jedem Fall dieselbe: die übermäßige Prime. Dahinter verbirgt sich u.a. die Möglichkeit zur konsistenten ›Alteration‹ mithilfe eines einzigen Operators #.

In zwei aufeinander aufbauenden Beiträgen[57] untersuchen Norman Carey und David Clampitt die ›Wohlgeformtheits‹-Eigenschaft. Diese präsupponiert die Generiertheit der Skala mithilfe eines einzigen Intervalls. Nummeriert man die Töne einerseits in der Reihenfolge ihrer Generierung (d.h. entsprechend dem Toncharakter) und andererseits nach aufsteigender Tonhöhe, und zwar vom selben Anfangston ausgehend, so induziert der Übergang von der einen zur anderen Nummerierung eine Permutation der Zahlen von 0 bis n-1, welche die 0 in sich selbst überführt. Tabelle 1 zeigt dies für die Quint-generierte Diatonik, wo beide Nummerierungen vom Ton F beginnen.

Tabelle 1: Illustration der Wohlgeformtheitseigenschaft anhand der Quint-generierten Diatonik

Der Wohlgeformtheitsbedingung zufolge muss diese Umnummerierung eine lineare Abbildung sein: eine Multiplikation (modulo n) mit der Anzahl der Tonschritte, die das Generator-Intervall über dem Ton mit der Nummer 0 ausfüllen. In der Tabelle ist die untere Zahl jeweils das Vierfache der oberen modulo 7. Die Wohlgeformtheitseigenschaft besagt also, dass alle Instanzen des generierenden Intervalls aus der gleichen Anzahl von Tonschritten bestehen. Die sechs Quinten von F bis H haben nicht nur dieselbe spezifische Größe, sondern tragen zu Recht auch allesamt den Namen ›Quinte‹, da sie alle mit vier Schritten ausgefüllt sind. Dies gilt dann sogar für die verminderte Quinte H-F.

Der Musikwissenschaftler Eytan Agmon untersucht einen Begriff von Diatonizität, der die soeben diskutierte Eigenschaft der Wohlgeformtheit einbezieht und noch zwei weitere Bedingungen hinzufügt: ›Effizienz‹ und ›Kohärenz‹, die anhand von Abbildung 1 erläutert werden.[58] Das zweidimensionale Koordinatensystem zeigt die dreizehn innerhalb eines Oktavrahmens unterscheidbaren diatonischen Intervalle von der reinen Prime (P1), über die kleine und die große Sekunde (m2 und M2) etc. bis hin zur der kleinen und der großen Septime (m7 und M7). Die horizontale Achse zeigt die spezifischen Zwölfton-Koordinaten dieser Intervalle (von 0 bis 11), während die vertikale Achse die generischen Siebenton-Koordinaten zeigt (von 0 bis 6). Die Wohlgeformtheitseigenschaft ist aus der Graphik allein nicht unmittelbar ersichtlich. Aber sie verbirgt sich hinter der folgenden Beobachtung Agmons: Beginnend von der verminderten Quinte d5 mit den Koordinaten (6, 4) über die kleinen Intervalle m2, m6, m3, m7, dann die reinen P4, P1, P5, und schließlich die großen M2, M6, M3, M7 bis zur übermäßigen Quarte A4 bilden die 13 Intervalle eine Quintenkette im Sinne beider Koordinatenachsen. Von jedem Intervall der Kette bis zum nächsten gelangt man durch Addition des Quintvektors (7, 4) modulo (12, 7).

Abbildung 1: Die 13 diatonischen Intervalle in spezifischen (horizontalen) und generischen (vertikalen) Koordinaten

›Effizient‹ nennt Agmon die Diatonik, weil tatsächlich jede der Zahlen 0 bis 11 auch als spezifische Koordinate in einem diatonischen Intervall vorkommt. Es gibt also aus Sicht der Diatonik keine überflüssigen chromatischen Intervalle. Lässt man dann entweder die verminderte Quinte oder die übermäßige Quarte aus dem Spiel, so stehen die verbleibenden zwölf diatonischen Intervalle sogar in eineindeutiger Beziehung zu ihren spezifischen Koordinaten. Die sich daraus ergebende Funktion, die jeder spezifischen Koordinate eine dann eindeutig bestimmte generische Koordinate zuordnet, ist darüber hinaus monoton steigend. Darin äußert sich die ›Kohärenz‹ des diatonischen Systems. Das Bestehen jener einzigen Ambiguität zwischen übermäßiger Quarte (6, 3) und verminderter Quinte (6, 4) hinsichtlich ihrer gemeinsamen spezifischen Koordinate 6 erachtet Agmon als Teil seines Diatonizitätsbegriffes.[59] In der Literatur wird dieser Diatonizitätsbegriff u.a. als ›diatonic property‹ bezeichnet.

Agmons Begriff impliziert eine weitere Eigenschaft, die von John Clough und Jack Douthett zum Ausgangspunkt weiterer umfangreicher Untersuchungen gemacht wird:[60] Die Verteilung der ›pitch classes‹ {0, 2, 4, 5, 7, 9, 11} innerhalb des Zwölftonsystems ist maximal regelmäßig. Dahinter steht eine Bedingung an die spezifischen Ausprägungen der generischen Intervalle, die sich von der schon diskutierten Myhill-Eigenschaft in zweierlei Hinsicht unterscheidet. Letztere wird einerseits gelockert in dem Sinne, dass jedem generischen Intervall höchstes zwei verschiedene Species entsprechen dürfen. Damit besteht die Möglichkeit, dass auch anderen Genera außer der Prim nur eine einzige Species entspricht. Diese gelockerte Myhill-Bedingung allein wird auch als ›Verteilungsregelmäßigkeit‹ bezeichnet. Andererseits kommt bei der maximalen Regelmäßigkeit eine zusätzliche Bedingung ins Spiel. Wenn einem generischen Intervall zwei Species entsprechen, dann sollen sich deren spezifische Intervallgrößen um genau einen chromatischen Schritt unterscheiden. Beispiele für maximal regelmäßige Skalen sind die Ganztonskala {0, 2, 4, 6, 8, 10} und die oktatonische Skala {0, 1, 3, 4, 6, 7, 9, 10}. Erstere ist völlig regelmäßig und damit auch in einem trivialen[61] Sinne wohlgeformt. Die oktatonische Skala hingegen ist nicht generiert und damit erst recht nicht wohlgeformt. Ein Beispiel für eine verteilungsregelmäßige, aber weder maximal regelmäßige noch wohlgeformte Skala ist die hexatonische {0, 1, 4, 5, 8, 9}.

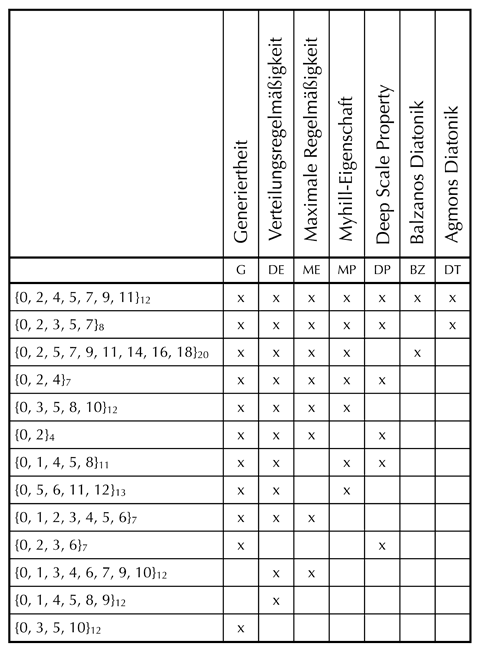
Eine Taxonomie der Skalen unter Berücksichtigung von acht solchen Merkmalen präsentieren John Clough, Nora Engebretsen und Jonathan Kochavi.[62] Zu den sieben schon genannten kommt dort ›Balzanos Diatonik‹, die im vorliegenden Beitrag nicht näher betrachtet wird. Die mathematische Teildisziplin, die sich auf der Metaebene mit solcherart taxonomischen Untersuchungen beschäftigt, ist die ›formale Begriffsanalyse‹.[63] Offenbar ohne Kenntnis der mathematischen Literatur liefern Clough und Coautoren ein überzeugendes Beispiel für deren Anwendung, die hier in der Sprache der formalen Begriffsanalyse kurz rekapituliert werden soll.

Zwischen einer Menge A von ›Objekten‹ und einer Menge M von ›Merkmalen‹ betrachtet man eine ›Indizenzrelation‹ I (Tabelle 2), die für jedes Objekt a und jedes Merkmal m festhält, ob m auf a zutrifft oder nicht. Diese Information lässt sich vorteilhaft in Form einer Tabelle festhalten mit einer Zeile für jedes Objekt, einer Spalte für jedes Merkmal und einem Kreuzchen in jeder Zelle, die eine Inzidenz zwischen dem betreffenden Merkmal und dem betreffenden Objekt repräsentiert. Dieses Datum (A, M, I) nennt man einen ›formalen Kontext‹.

Im Falle der Skalentaxonomie sind die betrachteten Objekte Teilmengen von chromatischen Tonsystemen, die durch endliche[64] zyklische Gruppen beschrieben werden. Letztere mag man sich einfach wie Zifferblätter von Uhren mit verschiedenen Stundenzahlen vorstellen. Die Kardinalität der Chromatik wird jeweils als Subindex der betreffenden Menge notiert. So bezeichnet {0, 2, 4, 5, 7, 9, 11}₁₂ die C-Dur-Tonleiter im 12-Tonsystem und {0, 2, 4}₇ den generischen Dreiklang auf der I. Stufe im 7-Tonsystem. Die folgende Tabelle zeigt einen ›reduzierten‹ formalen Kontext. Er wird von nur 13 Objekten und 7 Merkmalen aufgespannt und beinhaltet damit so wenig Objekte und Merkmale, wie nötig.

Tabelle 2: Reduzierter formaler Kontext von Skalen und Merkmalen zu den Begriffen der Diatonizität

Wenn nämlich mehrere Zeilen der Tabelle alle Kreuzchen in denselben Spalten haben, dann genügt es vollauf, nur eine davon in der Tabelle zu behalten. Bei den Merkmalen verzichtet man darüber hinaus auf Spalten, deren Kreuzchen genau den Durchschnitt anderer Spalten bilden. Deswegen kann die Spalte zum Wohlgeformtheitsmerkmal entfallen. Diese Bedingung ist logisch äquivalent zur Konjunktion aus Generiertheit und Verteilungsregelmäßigkeit.

Jeder formale Begriff besteht jeweils aus seinem ›Inhalt‹, d.h. einer Menge von Merkmalen, und seinem ›Umfang‹, einer Menge von Objekten. Beide Mengen sind gesättigt in dem Sinne, dass der Begriffsinhalt tatsächlich all diejenigen Merkmale umfasst, die auf alle Objekte des Begriffsumfangs zutreffen und der Begriffsumfang umfasst tatsächlich all diejenigen Objekte, die alle Merkmale des Begriffsinhalts aufweisen. Anschaulich bedeutet dies, dass die zugehörigen Kreuzchen in der Tabelle (nach geeigneter Umsortierung von Zeilen und Spalten) ein Rechteck bilden, welches weder horizontal noch vertikal erweiterbar ist. Dies bedeutet, dass in jeder nicht zum Umfang gehörigen Zeile in mindestens einer der zum Begriffsinhalt gehörigen Spalten ein Kreuzchen fehlt und in jeder nicht zum Inhalt gehörigen Spalte in mindestens einer der zum Begriffsumfang gehörigen Zeile ein Kreuzchen fehlt.

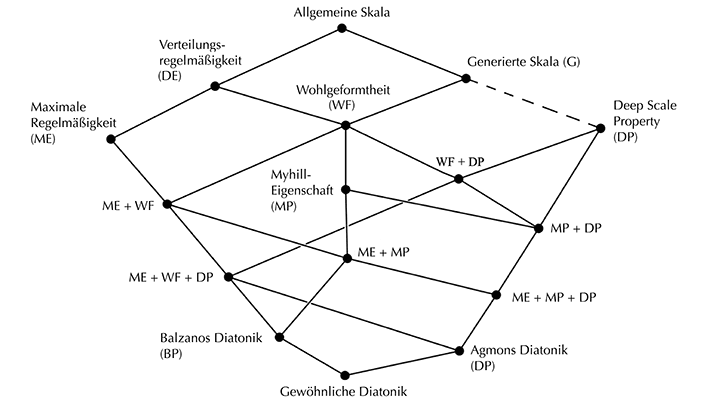
Im Falle des hier betrachteten Kontextes lassen sich fünfzehn solcher formalen Begriffe unterscheiden, denen man noch einen sechzehnten allgemeinen Dachbegriff mit leerem Inhalt hinzufügen kann. Den Begriffen wohnt eine Ordnungsrelation inne, die sich in Form eines Liniendiagramms veranschaulichen lässt. Jede Linie verbindet ein Begriffspaar, dessen unterer Begriff einen jeweils kleineren Umfang und dafür eine größere Merkmalsmenge besitzt als der obere.[65]

Abbildung 2: Formaler Begriffsverband zur Diatonizität, der sich aus dem formalen Kontext in Tabelle 2 ergibt

Innerhalb der verzweigten musiktheoretischen Untersuchungen zum Diatonizitätsbegriff lassen sich anhand dieses Begriffsverbandes zwei Interessensschwerpunkte ausmachen, die sich hinsichtlich ihrer Bevorzugung zweier Knoten als Grundbegriffe unterscheiden. Jene Ansätze, die sich in erster Linie dem Studium von Stimmführungen von ›pitch class sets‹ widmen, lassen eine stärkere Affinität zum Begriff der Maximalen Regelmäßigkeit erkennen – d.h., Begriffe mit stärkerem Inhalt, wie beispielsweise Agmons Diatonik, werden entsprechend als Spezialisierungen bzw. Verschärfungen der ME-Eigenschaft angesehen. Der vorliegende Beitrag bevorzugt hingegen einen Strang, der vom Begriff der Generiertheit ausgeht und über den der Wohlgeformtheit, der Myhill-Eigenschaft zu Agmons Diatonik führt. Dieser Strang befördert die Reinterpretation traditioneller Begriffe und Sachverhalte und steht ideengeschichtlich mit dem Begriff des Toncharakters in Verbindung. Die Auseinandersetzung mit den abstrakten Begriffen sollte eigentlich keinen Anlass für ein ›Schisma‹ unter den Theoretikern geben. Die Fixierung des Interesses auf Stimmführungsökonomie einerseits und auf innere Transformationen des Intervallsystems andererseits stellt aber dennoch eine bemerkenswerte Parallele zu Handschins Kritik an Stumpfs einseitiger Fixierung auf den Tonhöhenparameter dar und eröffnet die Perspektive einer interessanten Debatte um die kognitiven Interpretationen dieser Ansätze.

Die Wohlgeformtheitseigenschaft bringt eine Besonderheit mit sich, die im Zusammenhang mit dem Projekt einer kognitiven Deutung eine große Herausforderung darstellt und die ein interessantes Licht auf eine alte Kontroverse um den Toncharakter wirft. Diese Besonderheit ist zugleich der Ausgangspunkt für die weiteren Untersuchungen, die im dritten Abschnitt vorgestellt werden. Es geht um die Tatsache, dass die Konversion der Quintkoordinaten in die Schrittkoordinaten eine ›lineare Transformation‹ darstellt. Um die mögliche Tragweite dieses Sachverhalts zu verstehen, sei zunächst an einen von zwei[66] Einwänden erinnert, den Dahlhaus in den Untersuchungen gegen den Toncharakter vorbringt.

Die zweite der Folgerungen aus dem Rekurs auf die Quintenkette, die Behauptung, dass in der Quintenstruktur der Diatonik die kleine Terz drei, die große Terz vier und der Halbton fünf Quintabstände enthalte, ist, wenn nicht irrig, so doch ungenügend. Dass der Ganzton als Differenz zwischen Quarte und Quinte, die große Terz als Zusammensetzung von zwei Ganztönen und der Halbton als Differenz zwischen großer Terz und Quarte bestimmt wird, bedeutet nicht, dass die Quintbeziehung, die das System fundiert, in den Verzweigungen der Intervallableitungen, als dritte, vierte oder fünfte Quinte gegenwärtig sei. Man kann die Vermittlungen, an deren Ende der Halbton steht, in Gedanken rekonstruieren; die musikalische Wahrnehmung ist jedoch eng begrenzt: Für sie verschwinden die Voraussetzungen im Resultat. Man kann sich beim Hören eines Intervalls zwar die letzte Vermittlungsstufe bewusst machen, aber nicht die früheren, kann also Quarte und Quinte beim Ganzton oder die Ganztonverdopplung bei der großen Terz mitdenken, aber nicht vier Quinten bei der großen Terz.[67]

Dahlhaus lässt übrigens eine Vorgeschichte dieses Arguments unerwähnt, nämlich, dass Handschin selbst den Einwand, »der Sänger und Hörer könne doch beim Schritt c-e nicht fühlen, daß das e 4 Quintenschritte voraussetzte« schon bei Helmholtz vorfand und zum Anlass nahm, sich seinerseits zu fragen, ob es sich hier bereits um eine im 19. Jahrhundert vertretene Vorform der Kritik seines tonpsychologischen Ansatzes handelte.[68]

Da Handschin eher an eine unbewusste Wahrnehmung des Toncharakters denkt denn an eine bewusste Gehörbildungsübung, wie sie der Einwand unterstellt, geht letzterer zwar fehl, macht aber immerhin deutlich, dass hinsichtlich der Wechselbeziehung zwischen den beiden Koordinatensystemen eine Erklärungslücke besteht.

Dahlhaus selbst bringt diesbezüglich eine Überlegung ins Spiel, die ihrerseits eine transformationelle Perspektive provoziert. Er schließt eine verzweigte und kritische Erörterung des Verfahrens »die Modi durch die Skala und die Skala durch die Quintenkette zu begründen«[69] mit folgender Bemerkung:

Die modale und die abstrakte Darstellung der Diatonik sind zwei Seiten einer Sache, und der Gedanke, man müsse sich für einen Vorrang der einen oder der anderen Seite entscheiden, wäre ein Vorurteil – in der Vorstellung, es müsse immer ein erstes, fundierendes Phänomen geben, von dem dann ein zweites fundiertes, abzuleiten sei, steckt eine falsche Erwartung gegenüber der Wirklichkeit.[70]

Wenn man jenen ›Automorphismus‹, d.h. die innere Transformation des Systems, welche zwischen den beiden Seiten – den beiden Arten des Gegebenseins von Tonbeziehungen – vermittelt, als grundlegende Komponente des Begriffes von Diatonizität ansieht, so ergeben sich aus diesem Ansatz zwei Untersuchungsfelder. Aus Sicht der Musikkognition ergibt sich die Frage nach der kognitiven Realität hinter solchen Koordinatentransformationen. Aus Sicht der mathematischen Musiktheorie ergibt sich die Frage nach weiteren logischen Konsequenzen und deren musiktheoretischen Bedeutungen. Bei dem nun folgenden Versuch, traditionelle Begriffe der Diatonizität mit ausgewählten Knoten des obigen Begriffsverbandes in Verbindung zu bringen, spielt deshalb die Beantwortung dieser zweiten Frage eine Schlüsselrolle.

3. Algebraische Kombinatorik der Modi und Hexachorde

Die Präsupposition des 12-tönigen chromatischen Referenzsystems, welche die im zweiten Abschnitt behandelten Begriffe in das Korsett der ›pitch class theory‹ zu zwängen scheint, mag den Eindruck erwecken, als seien diese neuen Begriffe der Diatonizität ohne jede Verankerung in den traditionellen Begriffen, wie etwa den pseudo-klassischen Modi des Mittelalters, dem Drei-Hexachord-System des Spätmittelalters und der Frührenaissance oder der Oktavregel, dem Drei-Dreiklangs-System bzw. dem Sieben-Stufen-System der neuzeitlichen harmonischen Tonalität. Die abstrakte mathematische Begriffsanalyse kann dabei helfen, den vorgreifenden Anachronismus als sinnvolles Gedankenexperiment zu enttabuisieren, indem sie logische Abhängigkeiten unter die Lupe nimmt. Für jeden der neueren Begriffe kann zunächst geprüft werden, ob diese Präsupposition ggf. gelockert werden kann, ohne den jeweiligen Begriff zu verzerren.

Beispielsweise lässt sich im chromatischen Intervallsystem die Annahme der Oktavidentifikation, d.h. die Identifikation der Oktave und ihrer Vielfachen mit der Prime, problemlos aufgeben, solange nur solche Transformationen betrachtet werden, die sich in geeigneter Weise ›anheben‹ lassen. In der nachstehenden Sequenz[71] von Abbildungen sind die Vielfachen der Oktave eingebettet in die chromatischen Intervalle, die ihrerseits auf die zugehörigen ›pitch-class‹-Intervalle abgebildet werden.

Jeder der formalen Begriffe lässt sich von ›pitch-class‹-Skalen auf oktavperiodische Skalen innerhalb eines entsprechenden chromatischen Referenzsystems beziehen. Etwas schwieriger ist dagegen die Frage nach der Präsupposition eines chromatischen Referenzsystems an sich. Für die Definition des Kriteriums der maximal regelmäßigen Verteilung spielt es jedenfalls eine unverzichtbare Rolle und der Begriffsknoten mit der Bezeichnung ›Maximale Regelmäßigkeit‹ lässt sich damit nicht ohne interpretatorischen Gewaltstreich auf Notations-basierte musiktheoretische Begriffe übertragen.

Ganz anders verhält es sich mit der Wohlgeformtheitseigenschaft, der eng damit verbundenen Myhill-Eigenschaft und mit allen Spezialisierungen derselben. Auf den ersten Blick scheint es zwar, dass die Wohlgeformtheitsbedingung den Spielraum für Lockerungen sogar noch weiter einschränkt, weil ja das generische Intervallsystem, auf dem jener lineare Automorphismus definiert ist, ebenfalls nach dem Vorbild der ›pitch-class‹-Intervalle gebaut ist.[72] Es sind also beide Referenzsysteme, das generische und das spezifische, die es in geeigneter Weise zu modifizieren gilt, um den traditionellen Begriffen der Diatonizität näher zu kommen. Einen geeigneten Theorieentwurf dazu hat Eric Regener vorlegt[73], noch vor dem Aufkommen der Diatonic Set Theory. Carey und Clampitt (1989, 1996a) schaffen eine erste Brücke zu Regeners Ansatz, indem sie die Wohlgeformtheits- und die Myhill-Eigenschaften für beliebige reelle Intervallgrößen formulieren und damit auf ein spezifisches chromatisches Referenzsystem verzichten.[74] Von großer musiktheoretischer Bedeutung ist der von Carey und Clampitt erbrachte Nachweis, dass für alle Skalen, die nicht völlig regulär sind, die Eigenschaft der Wohlgeformtheit zur Myhill-Eigenschaft logisch äquivalent ist. Dass die beiden Begriffsknoten nicht sogar zusammenfallen, liegt einzig an den völlig regulären Skalen, die zwar zur Extension des Wohlgeformtheitsbegriffs, nicht aber zur Extension des mit der Myhill-Eigenschaft assoziierten formalen Begriffs gehören.[75]

Nun gilt es, die Wohlgeformtheitsbedingung von generischen Stufen auf die Beschreibungsebene von ›Notenintervallen‹ zu heben. Die mathematische Ausarbeitung dazu findet sich bereits in Kapitel 8 von Regeners Buch.[76] Das nachstehende Diagramm verbindet diese mit derjenigen von Carey und Clampitt. Der mittlere Ausdruck in der unteren Zeile Z·M2 x Z·m2 bezeichnet die Menge aller Notenintervalle und zwar als Linearkombinationen aus großen und kleinen Sekunden (M2 bzw. m2). Der mittlere Ausdruck in der oberen Zeile Z·P5 x Z·P4 bezeichnet ebenfalls die Menge aller Notenintervalle, aber in diesem Falle als Linearkombinationen aus reinen[77] Quinten P5 und reinen Quarten P4. Jedes Notenintervall hat dann eine eindeutige Repräsentation in Form von Quint-Quart-Koordinaten und eine eindeutige Repräsentation in Form von großen/kleinen Sekund-Koordinaten. Die Umrechnung der ersteren in die letzteren entspricht einer linearen Transformation auf der Menge Z x Z der Paare ganzer Zahlen. Sie wird durch jene 2x2-Matrix repräsentiert, die im Diagramm neben dem vertikalen Pfeil eingetragen ist.

Die beiden Spaltenvektoren[78] (3, 1)^T und (2, 1)^T der Transformationsmatrix repräsentieren die Schritt- oder Sekundkoordinaten von Quinte P5 und Quarte P4. Die Quinte setzt sich aus drei Ganztönen M2 und einem Halbton m2 zusammen, die Quarte aus zwei Ganztönen und einem Halbton.

Die Spaltenvektoren (1, 1)^T bzw. (3, -4)^T weiter links in der oberen Zeile des Diagramms bezeichnen jeweils die Quint-Quart-Koordinaten der Oktave P8 bzw. der übermäßigen Prime A1. Die Transformationsmatrix überführt[79] sie in die zugehörigen Spaltenvektoren mit den Schrittkoordinaten (5, 2)^T bzw. (1, -1)^T.

Reine Oktaven, übermäßige Primen und deren Linenarkombinationen sind nun genau jene Intervalle, die im generischen 7-Stufen-System Z₇ übergangen werden und die unter den mit horizontalen Pfeilen bezeichneten Abbildungen Z·P5 x Z·P4 -> Z₇ bzw. Z·M2 x Z·m2 -> Z₇ auf Null abgebildet werden. Folglich ist Regeners Transformation eine Anhebung des Wohlgeformtheits-Automorphismus von generischen Stufen-Intervallen auf den Bereich aller Noten-Intervalle.

Damit erhält der durch das (nicht-degenerierte) Wohlgeformtheitsmerkmal erfasste Diatonizitätsbegriff eine flexiblere und robustere Form. Mit Hilfe der Transformation, welche P5-P4-Koordinaten in M2-m2-Koordinaten überführt, können nicht nur diatonische Intervalle, sondern auch deren Oktav-Versetzungen und Alterationen verrechnet werden.

In der Verallgemeinerung besteht das generierende Intervall aus k primären Schritten und m sekundären Schritten und sein Oktavkomplement aus l primären Schritten und n sekundären Schritten. Die Transformationsmatrix hat dann die Gestalt

und erfüllt die Bedingung det(M) = kn - lm = 1. Der formale Begriff mit der Bezeichnung ›Myhill-Eigenschaft‹ erhält damit aufgrund der logischen Äquivalenz zur nicht-degenerierten Wohlgeformtheit eine weitere musiktheoretische Aufwertung, insofern er auch die Arithmetik der traditionellen musikalischen Notation einbezieht.

Ausgehend von diesem Zwischenergebnis können nun auch die ›pseudo-klassischen Modi‹[80] unter einem transformationellen Gesichtspunkt betrachtet werden. Die mathematischen Erkenntnisse lassen dabei mehrere teilweise kontrovers diskutierte Fragen in einem neuen Licht erscheinen und suggerieren neue Beantwortungsmöglichkeiten. Dazu gehört Dahlhaus’ Kritik an Handschins Sicht auf die Rolle des Toncharakters bei den Modi, die Verortung des Tones b in der ›musica recta‹ und die damit verbundenen Fragen nach dem Verhältnis von Diatonik und dem Drei-Hexachord-System und der Einordnung der ›musica ficta‹.

Zunächst sollen die modalen Quint- und Quartgattungen und die aus ihnen zusammengesetzten Oktavgattungen[81] als Transformationen beschrieben werden und zwar als weitere Verfeinerung jener mit der obigen 2x2-Matrix M beschriebenen linearen Intervalltransformation. Während nämlich die beiden Spaltenvektoren (3, 1)^T und (2, 1)^T der Transformationsmatrix die bloßen Anzahlen an großen und kleinen Sekunden angeben, aus denen sich die reine Quinte bzw. die reine Quarte zusammensetzen, legen die Quint- und Quartgattungen jeweils eine spezifische Reihenfolge fest, in der die Schrittintervalle die jeweiligen Rahmenintervalle ausfüllen. Mathematisch bedeutet dies den Übergang von einem kommutativen zu einem nicht-kommutativen Intervallsystem. Anstelle der Spaltenvektoren mit jeweils zwei Koordinaten, deren Addition kommutativ ist, werden im nicht-kommutativen Fall Wörter miteinander verknüpft.

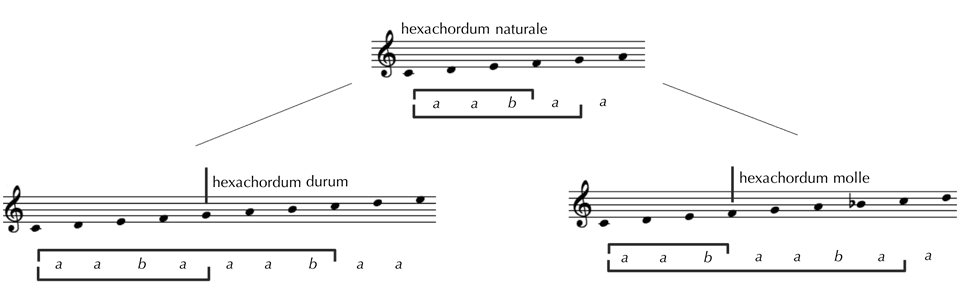
Das Alphabet, über dem diese Wörter gebildet werden, hat nur zwei Buchstaben: a und b. Sie stehen jeweils für ein primäres und ein sekundäres Elementar-Intervall: Quinte und Quarte bzw. große und kleine Sekunde. Die primären Intervalle zeigen auf der Quintenachse in Kreuz-Richtung, und die sekundären zeigen in Be-Richtung. Die aus a und b gebildeten Wörter, wie a, aa, ab, aab, aabaa usw. repräsentieren jeweils musikalische Intervalle und zwar als Resultate der Verkettung von primären und sekundären Elementar-Intervallen. Es wäre irreführend, diese Wörter als fixierte Namen zu betrachten. Diese Verkettungsregeln verhalten sich vielmehr wie Zahlen, welche mal die eine, mal die andere Größe repräsentieren und an die man sowohl Namen als auch ›musikalische Einheiten‹ binden müsste, um eine gewählte Repräsentation sicher zu fixieren.[82] Wenn Quinte und Quarte die Rolle der Elementar-Intervalle spielen, stehen sowohl ab bzw. ba für die Oktave, und zwar für deren authentische bzw. plagale Zusammensetzung. Wenn große und kleine Sekunde die Rolle der Elementar-Intervalle spielen, stehen ab bzw. ba für die kleine Terz, und z.B. aabaa für die große Sexte in der Zusammensetzung von Guidos Hexachord.

Jeder der sechs[83] authentischen diatonischen Modi stellt eine Verbindung her zwischen der Zusammensetzung der Oktave aus Quinte und Quarte mit deren Ausfüllung durch die jeweiligen Gattungen von Quinte und Quarte. Zur besseren Bezeichnung der Teilung der Oktave wird im Folgenden ein Trennstrich verwendet. Für die authentische Teilung a|b ergeben sich im Einzelnen die folgenden Paare aus Quint- und Quartgattungen:

Tabelle 3: Die Schrittintervallmuster der sechs authentischen Modi

Diese Modi können als Transformationen auf Wörtern interpretiert werden. Während die Matrix

P5-P4-Koordinaten in M2-m2-Koordinaten überführt, werden nun Wörter, welche Verkettungen von Quinten und Quarten repräsentieren, in zugehörige Wörter überführt, welche die entsprechenden Verkettungen von großen und kleinen Sekunden beschreiben. In diesem Sinne ist jedes der sechs Wortpaare in der Tabelle eine Verfeinerung der Transformationsmatrix M, deren Koordinaten ja nur die Anzahlen von ›a’s‹ und ›b’s‹ vor und nach dem Teilungsstrich kodiert, nicht aber deren Reihenfolge.

In der für diese Untersuchungen zuständigen mathematischen Spezialdisziplin Algebraische Kombinatorik auf Wörtern[84] findet man zwei transformationelle Standpunkte vor. In einem ersten Schritt genügt es, sich mit den ›Sturm’schen Morphismen‹ vertraut zu machen, welche auf der Menge {a, b}* aller endlichen Wörter operieren, die aus den beiden Buchstaben a und b gebildet werden können. In einem zweiten Schritt ist es dann erforderlich, die algebraisch etwas verwickeltere Auffassung dieser Sturm’schen Morphismen als Automorphismen der freien (nicht-kommutativen) Gruppe F₂ mit zwei Erzeugenden a und b zu betrachten.

Die Sturm’schen Morphismen sind spezielle Ersetzungsregeln, bei denen die beiden Buchstaben a und b jeweils durch passend aufeinander abgestimmte Wörter substituiert werden. Diese werden dann – Buchstabe für Buchstabe – auch auf ganze Wörter angewandt – vergleichbar mit der ›Suche und Ersetze‹-Funktion eines Texteditors. Die Bedingungen an die Ersetzungsregeln der Sturm’schen Morphismen sind allerdings sehr streng, uns es ist aus Sicht der Mathematik erstaunlich, dass sie von den modalen Quint- und Quartgattungen erfüllt werden. Die nachstehenden vier Ersetzungsregeln erzeugen qua iterative Verkettung die ›Speziellen Sturm’schen Morphismen‹:

Die nachstehende Auflistung zeigt, wie sich jeder der sechs authentischen Modi als Bild der authentischen Teilung der Oktave a|b unter einem speziellen Sturm’schen Morphismus ergibt:

Die Zerlegung dieser Morphismen in die Generatoren G, G^~, D und D^~ bringt eine Zerlegung des Transformationsaktes mit sich, deren Zwischenergebnisse sich in einen sinnvollen Zusammenhang mit einer prominenten historischen Ableitung der Modi bringen lässt. Dahlhaus favorisiert sie in seinen Untersuchungen im Zusammenhang mit seiner Kritik an Handschins »Verfahren, die Modi durch die Skala und die Skala durch die Quintenkette zu begründen«.

Das Prinzip, das man der Diatonik in ihrer konkreten Beschaffenheit zugrunde legen muß, ist demnach die Ausfüllung eines Quart-Quint-Oktav-Gerüstes durch Ganztöne. Das Resultat der Ausfüllung aber ist ein Modus; oder anders formuliert: die Diatonik erscheint, wenn man sie durch Ausfüllung eines Quart-Quint-Oktav-Gerüstes konstruiert, in modaler Gestalt. […]

Die Konstruktion der älteren modalen Diatonik aus Tetrachorden ist die geschichtlich früheste und auch die sachlich am festesten begründete Methode.[85]

Für die Ionischen, Dorischen und Phrygischen Modi entsprechen die transformationellen Zwischenstationen genau diesem Prinzip. Zunächst wird durch Anwendung des Morphismus D aus der authentischen Teilung ein Quart-Quint-Oktav-Gerüst und dann werden die beiden leeren disjunkten Quarten auf die gleiche Weise mit Ganztönen zu Tetrachorden gefüllt. Der Halbton entsteht dabei als Restintervall. Für die Lydischen, Mixolydischen und Äolischen Modi entsteht durch Anwendung des Morphismus D^~ zunächst ein Sekund-Quint-Oktav-Gerüst mit konjunkten leeren Quarten, die dann ebenfalls auf die gleiche Weise mit Ganztönen zu Tetrachorden ausgefüllt werden. Würde man auch bei diesen drei Modi auf einem Quart-Quint-Oktav-Gerüst bestehen, dann würde die Ausfüllung der Quarten durch jeweils gleiche Tetrachorde keine Berücksichtigung finden und damit würde man Guidos Affinitätsprinzip nicht gerecht.

Die Lokrische Oktavgattung baabaaa, die ebenfalls zu den obigen sechs konjugiert ist, kann nicht mit Hilfe eines Morphismus erzeugt werden. In der mathematischen Literatur trägt dieser Sonderfall die Bezeichnung ›the bad conjugate‹.

An dieser Stelle sei nun an den ersten der beiden Einwände erinnert, die Dahlhaus gegen Handschins Verfahren, den Modi die Quintenkette zugrunde zu legen, vorbringt:

Als Normen musikalischen Hörens sind die Konsequenzen nicht unproblematisch. Denn daß der Ton e, wenn er als 1. Stufe des e-Modus exponiert und als 2. Stufe des d-Modus weitergeführt wird, seine Bedeutung ändert, dürfte kaum zu leugnen sein. Und die These, daß dennoch der Charakter des Tones e primär durch die Stellung in der Quintenkette geprägt sei, ist nur durch den Zusatz zu retten, daß der Toncharakter den Modus zwar verdeckt und modifiziert, aber nicht aufgehoben werde. Doch wäre einzuwenden, daß eine Modifikation, die den Charakter verdeckt, in einer Musiktheorie, die Phänomene zu beschreiben versucht, von einem Wechsel des Charakters nicht zu unterscheiden ist.[86]

Der Einwand berührt zu Recht eine Diskrepanz zwischen der durch die Wortbedeutung des Ausdrucks ›Toncharakter‹ miterfassten und musiktheoretisch relevanten Unterscheidbarkeit von wechselnden modalen Stufenbedeutungen ein und desselben Tones einerseits und der abstrakten theoretischen Verortung des Toncharakters in Handschins Ansatz als fixierte Position in der Quintenkette andererseits. Dahlhaus’ spitzfindige Auswertung dieser Diskrepanz ist allerdings wenig hilfreich. Handschins These, dass dennoch der Charakter eines Tones primär durch die Stellung in der Quintenkette geprägt sei, lässt sich mathematisch mithilfe von modalen Verfeinerungen der Quintenkette retten, denen nach wie vor die Quintenkette als Essenz innewohnt.

Ganz nach dem Vorbild der vier Quintgattungen und der drei Quartgattungen, die sich bei passender Wahl zu den modalen Oktavgattungen zusammensetzen, lassen sich auf der Seite des Toncharakters zwei Gattungen der großen und fünf Gattungen der kleinen Sekunde als Quint-Quart-Faltungen unterscheiden. Bedingung für die Konstruktion der Faltungen ist, dass die Töne den Ambitus einer Oktave nicht überschreiten:

Abbildung 3: Die Gattungen der großen und kleinen Sekunden

Um die diatonische Quintenkette durch Quint-Quart-Faltungen zu verfeinern, lassen sich bei passender Wahl je eine Gattung der großen Sekunde und eine Gattung der kleinen Sekunde zu einer Gattung der übermäßigen Prime zusammensetzen. Die Richtungen der beiden Sekundintervalle sind dabei entgegengesetzt.

Das nachstehende Notenbeispiel zeigt links den authentischen Dorischen Modus und rechts zwei alternative Faltungen, denen gemein ist, dass sie beide den Ambitus des Dorischen Modus ausfüllen, ohne die Oberoktave der Finalis zu berühren. Sie unterscheiden sich jedoch in der Richtung. Die obere Faltung verläuft von f nach f# in Kreuz-Richtung und die untere verläuft von h nach b in Be-Richtung.

Abbildung 4: Der authentische Dorische Modus (links) und seine beiden Quint-Quart-Faltungen (rechts) in Kreuz- bzw. in Be-Richtung

Nach dem ersten Vortrag des Autors zu diesem Ansatz im Jahre 2007, in welchem die obere der beiden Faltungen zur Diskussion gestellt wurde, wies Hartmut Fladt darauf hin, dass die historisch ›richtigere‹ Faltung eigentlich jene in Be-Richtung sein sollte. Entgegen den damaligen Erwartungen des Autors zeigt die folgende algebraische Untersuchung, dass die historisch ›richtigere‹ Wahl auch aus mathematischer Sicht bevorzugt ist. Der Weg zu dieser Einsicht berücksichtigt darüber hinaus auf mathematische Weise Dahlhaus’ Bedenken gegen die »Vorstellung, es müsse immer ein erstes, fundierendes Phänomen geben, von dem dann ein zweites fundiertes, abzuleiten sei«.[87] Um nämlich die Quint- und Quartgattungen einerseits und die großen und kleinen Sekundgattungen andererseits als zwei Seiten einer Medaille zu kontrollieren, kann man wie folgt vorgehen:

Als Automorphismus der freien (nicht-kommutativen) Gruppe[88] F₂ besitzt der mit dem Dorischen Modus abaa | aba assoziierte Sturm’sche Morphismus einen dazu inversen Automorphismus. Zu seiner Berechnung substituieren wir x = abaa, y = aba und erhalten durch Einsetzen x = ya bzw. a = y^-1x. Setzt man diesen Ausdruck für a in y = aba ein, ergibt sich y = y^-1xby^-1x und durch Umstellen b = x^-1yyx^-1y. Der Vergleich mit dem Notenbeispiel zeigt, dass der inverse Automorphismus der unteren Faltung in Be-Richtung entspricht. Die Gattung a^-1=x^-1y des fallenden Ganztons wird gefolgt von der Gattung b = x^-1yyx^-1y des steigenden Halbtons. Eine bloße Tonhöhen-Umkehr der unteren Faltung ergibt jedoch nicht die obere Faltung. Für alle Glarean’schen Modi ergibt sich ein analoges Resultat. Die Be-Richtung ist aus algebraischer Sicht der Normalfall und die Kreuz-Richtung ist ihr gegenüber als Abweichung markiert.

Ob diese Feststellung von musiktheoretischer oder sogar kognitiver Relevanz ist, kann nicht ohne Weiteres entschieden werden. Aufgrund der mathematischen Dualität zwischen Oktave und übermäßiger Prime als Begrenzungsintervalle des Modus bzw. von dessen Quint-Quart-Faltung wird durch das Ergebnis die Deutung der b-Stufe als unselbstständige Variante der h-Stufe ins Spiel gebracht. Daneben gibt es eine rein äußerliche Parallele zur traditionellen Markiertheit der ›musica ficta‹ gegenüber der ›musica recta‹. Die Legitimation des Tones b als Bestandteil des mittelalterlichen Stammtonvorrats erfolgt im Spätmittelalter nicht direkt über die Modi, sondern über das Drei-Hexachord-System. Eine musiktheoretische Interpretation des obigen Resultats erfordert deshalb zunächst eine entsprechende Durchdringung des Verhältnisses von Diatonik und Drei-Hexachord-System und zwar aus musiktheoretischer und aus mathematischer Sicht.

Der Historiker Stefano Mengozzi[89] kritisiert vehement die Auffassung von einer hexachordalen Periode in der Musikgeschichte, der zufolge die Hexachord-Solmisation nicht nur eine pädagogische Hilfskonstruktion gewesen wäre, ein rein pädagogisches Darstellungsmittel, sondern auch eine genuin musikalische Anschauungsform. Einer der Adressaten seiner Kritik ist Dahlhaus:

Hexachordal theory had played an important role in Carl Dahlhaus’ theory of harmonic tonality. Dahlhaus took the structural differences between the hexachordal articulation of musical space and the modern, octave-based one as a negative indicator of the presence of tonal thinking in early music. In other words, modern tonality could not have emerged as long as that model of diatonic space, in the form of the late-Renaissance ›modal-hexachordal system‹, regulated the world of musical practice. At the end of his study, Dahlhaus offered numerous analyses of Renaissance polyphonic works by Josquin, Monteverdi, and others, moving from the premise of the hexachord as a basic principle of pitch organization. Dahlhaus’ readings of Monteverdi’s madrigals proposed a ›harmonic‹ reinterpretation of the Guidonian hexachord, by which each note of the six-fold set functioned as the root of a chord.[90]

Die Auswertung dieses Standpunktes muss in mehrere Richtungen erfolgen. Zur Aufrechterhaltung seiner Polarisierung zwischen Apologeten der Diatonik und solchen der Hexatonik lässt sich Mengozzi auf zwei illegitime Vereinfachungen ein, denen zunächst ein differenziertes Bild zur Seite gestellt werden soll. Eine betrifft den Status des Hexachords als Konfiguration von Tönen, die andere betrifft den Status des Hexachords als einer ordnenden Struktur hinter der Familie der authentischen Modi, gewissermaßen als ›halbes‹ Dodekachordon.

Mit dem besonderen Verweis auf die Oktavbasiertheit der Diatonik unterstellt Mengozzi, dass die Hexachord-Theoretiker das Hexachord als eine sechstönige Skala ansehen, die dann der sieben-tönigen diatonischen Skala ihren berechtigten Status als dem Tonsystem zugrunde liegende Skala streitig macht. Dahlhaus zeichnet demgegenüber ein wesentlich differenzierteres Bild:

Die Pentatonik und die Heptatonik sind Systeme. Das Hexchord ist dagegen eine bloße Hilfskonstruktion. Als System wäre es in sich widerspruchsvoll: Das Verfahren, zwar die Terz d-f, aber nicht die Terz a-c¹ durch eine Zwischenstufe auszufüllen, hätte, als Systemprinzip begriffen, die absurde Konsequenz, daß der Hörer zwischen den Intervallvorstellungen der Pentatonik und der Heptatonik, also zwischen der Auffassung der kleinen Terz als ›Schritt‹ und als ›Sprung‹ wechseln muß.[91]

Am Rande sei an dieser Stelle angemerkt, dass diese Argumentationsweise ganz und gar dem Denken in der mathematischen Musiktheorie entspricht. Vom ›Widerspruch‹ in einer Skala spricht man heute, wenn ein Intervall aus mehr Schritten besteht als ein anderes und trotzdem kleiner als jenes ist. Indessen spricht man von einer ›Ambiguität‹, wenn zwei gleichgroße Intervalle in der Zahl der Tonschritte differieren. Jene Systemeigenschaft, die Dahlhaus bei der Pentatonik und Heptatonik als erfüllt und beim Hexachord als verletzt ansieht, nennt man heute ›Kohärenz‹. Während Agmons Diatonizitätsbegriff eine einzige[92] Ambiguität vorsieht, finden sich im Hexachord dagegen viele Ambiguitäten, insbesondere auch die zwischen Sekunden und Terzen, die Dahlhaus hier problematisiert.

Eine Angriffsfläche aus Mengozzis Perspektive dürfte dann jedenfalls nicht das einzelne Hexachord, sondern allenfalls Dahlhaus’ Charakterisierung des Drei-Hexachord-Systems bieten.

Das Drei-Hexachord-System, die Verschränkung der Hexachorde durum (G-e, g-e¹, g¹-e²), naturale (c-a, c¹-a¹) und molle (f-d¹, f¹-d²), war die Darstellungs- und Anschauungsform des Tonsystems im späten Mittelalter. Durch den Ton b aber, der im Drei-Hexachord-System keine chromatische Variante zu h, sondern eine selbständige Stufe bildet, scheint die Geschlossenheit der modalen Diatonik sogar gestört oder sogar aufgehoben zu werden.[93]

Indem Dahlhaus von der »Darstellungs- und Anschauungsform« spricht und zudem den Ausdruck ›System‹ gebraucht, verleiht er dem Drei-Hexachord-System auch eine genuin musikalische Bedeutung. Sonst gäbe es auch keinen Anlass, ein Moment möglicher Inkompatibilität desselben mit der modalen Diatonik aufzuspüren und ausführlich zu diskutieren: den Status des Tones b.

Aus Sicht der algebraischen Kombinatorik auf Wörtern besteht zwischen Hexachord und Diatonik ein einfacher und sehr enger Strukturzusammenhang, dessen allgemeine Gültigkeit sich auf alle Skalen erstreckt, die zum formalen Begriff der Myhill-Eigenschaft gehören.[94]

Das Schrittmuster des Hexachords aabaa besitzt zwei besondere Präfixe: die Ioninsche Quintgattung aaba und die Ionische Quartgattung aab. Das Besondere daran ist die Tatsache, dass das Hexachord seinerseits Präfix von Potenzen beider Gattungen ist, also sowohl von den konjunkten Pentachorden (aaba)(aaba)… als auch von den konjunkten Tetrachorden (aab)(aab)… Das Hexachord ist deshalb Instanz einer besonderen Klasse von Wörtern, die als ›zentrale Palindrome‹ bezeichnet werden. Es sind die Grenzfälle des Theorems von Fine und Wilf[95], welches die Möglichkeit des Nebeneinanderbestehens zweier Periodizitäten in ein und demselben Wort untersucht. Die zentralen Palindrome sind die längsten Wörter mit dieser Eigenschaft. Sie bilden einen unendlichen binären Baum – den ›zentralen Baum‹ –, dessen Konstruktion auf der Methode der ›iterierten Palindromisierung‹[96] beruht: Aus einem bereits gegebenen zentralen Palindrom entstehen seine zwei Nachfolger durch Palindromisierung nach Anhängen der Buchstaben a bzw. b.

Die Palindromisierung von (aabaa)a ist aabaaabaa und sie entsteht auch durch Anhängen des Hexachords aabaa an die Ionische Quintgattung aaba. Der eine Nachfolger-Knoten aabaaabaa von aabaa im zentralen Baum entspricht damit dem Intervallmuster des Zwei-Hexachord-Systems aus ›hexachordum naturale‹ und ›hexachordum durum‹. Seine beiden Perioden werden durch die Ionische Quintgattung und die authentische Ionische Oktavgattung aabaaab gebildet.

Die Palindromisierung von (aabaa)b ist aabaabaa und sie entsteht auch durch Anhängen des Hexachords aabaa an die Ionische Quartgattung aab. Der andere Nachfolger-Knoten aabaabaa von aabaa entspricht damit dem Intervallmuster des Zwei-Hexachord-Systems aus ›hexachordum naturale‹ und ›hexachordum molle‹. Seine beiden Perioden werden durch die Ionische Quartgattung und die plagale Ionische Oktavgattung aabaaba gebildet.

Dem Drei-Hexachord-System entspricht also aus mathematischer Sicht die Spaltung des Knotens aabaa im zentralen Baum in seine beiden Nachfolger aabaaabaa und aabaabaa. Genaugenommen wäre dann der Ausdruck ›Drei-Hexachord-System‹ etwas grob, denn im Kern geht es um die Verbindung der beiden Zwei-Hexachord-Systeme in ihrem gemeinsamen Vorgängerknoten, dem ›hexachordum naturale‹.

Abbildung 5: Das Drei-Hexachord-System als Verzweigung des ›hexachordum naturale‹ in zwei Zwei-Hexachord-Systeme

Das Gemeinsame der beiden Knoten drückt sich in der Oktav-Periodizität aus, die zum einen im authentischen und zum anderen im plagalen Ionischen Modus exemplifiziert wird. Von einer mutmaßlichen Vernachlässigung der diatonischen Oktavperiodizität kann also beim Drei-Hexachord-System keine Rede sein. Nur sind die zentralen Palindrome keine Skalen, sondern Regionen[97], deren doppelte Periodizität die Option einer Weichenstellung beinhaltet. Damit ist Dahlhaus’ Charakterisierung gut mit den mathematischen Befunden in Einklang zu bringen. Sein Verweis auf die Idee einer gespaltenen Stufe[98] b/h entspricht der Verzweigung des zentralen Baumes beim ›hexachordum naturale‹.

Für jede Instanz des formalen Begriffes der Myhill-Eigenschaft gibt es einen verallgemeinerten Ionischen Modus. Dessen (verallgemeinerte) Quint-, Quart- und Oktavgattungen sind jene Wörter, die von den beiden speziellen Sturm’schen Morphismen G und D erzeugt werden. In der Literatur heißen diese (spezielle) Standard-Morphismen und die Bilder f(a) bzw. f(b) der beiden Buchstaben a bzw. b unter diesen Standard-Morphismen f heißen (spezielle) Standard-Wörter. Jedes geordnete Paar (f(a), f(b)) repräsentiert die beiden Präfixe eines zugehörigen zentralen Palindroms w, welche dessen zwei Perioden exemplifizieren. Die authentische Oktavgattung f(ab) stimmt mit dem Wort wab überein (d.h. das Wort w verlängert um das Suffix ab), und die plagale Oktavgattung f(ba) stimmt mit dem Wort wba überein. Die Vertauschung der letzten beiden Buchstaben ab versus ba entspricht dabei dem Effekt der Stufenspaltung. Die beiden Varianten der gespaltenen vorletzten Stufe des Modus sind zugleich die Begrenzungstöne der Faltung des authentischen Modus in Be-Richtung.

Dieses Resultat stützt die These einer sehr engen Strukturbeziehung zwischen den beiden Auffassungsformen des Tonsystems – der modalen und der hexachordalen. Einerseits stärkt sie die Plausibilität von Mengozzis These von einer ungebrochenen Tradition der oktav-periodischen Diatonik als Basis für die Konstitution von Tonbeziehungen. Andererseits erweist sich gleichzeitig dessen Sorge als unbegründet, dass die Hexachord-Theoretiker sich zu weit auf Abwege begeben haben könnten. Vielmehr bietet sich aus mathematischer Sicht die Möglichkeit einer zwanglosen Integration beider Auffassungen auf jenem Allgemeinheitsgrad, der hinter dem Begriff der Myhill-Eigenschaft steht.

An dieser Stelle sei auch an die Perspektive einer kognitiven Interpretation jenseits der abstrakten Integration musiktheoretischer Begriffe erinnert. Die Suche nach einem möglichen Zusammenhang zwischen der algebraischen Markiertheit der Kreuz-Richtung gegenüber der Be-Richtung einerseits und der musikalischen Markiertheit der ›musica ficta‹ gegenüber der ›musica recta‹ andererseits sollte sich von der Tatsache leiten lassen, dass sich erstere in prominenter Weise in der Sopranklausel manifestiert. Damit lässt sich die Untersuchungsrichtung in empirischer Hinsicht fokussieren. Den einschlägigen und wenig ergiebigen Erklärungsansätzen zur Kadenz würde eine dynamische Interpretation zur Seite gestellt, die sich auf eine Interpretation der Quint/Quart bzw. der beiden Sekundparameter als ›konjugierte Variable‹ beruft.[99]

Um die Diskussion zum Hexachord abzuschließen, muss noch jene zweite bereits benannte illegitime Vereinfachung in Mengozzis Argumentation angesprochen werden. Was dieser eine ›harmonische‹ Reinterpretation von Guidos Hexachord nennt, ist bei Dahlhaus keineswegs nur eine Menge von sechs Akkordfundamenten. Vielmehr handelt es sich um eine ›geschlossene Sozietät‹ von Teiltonarten, deren Kadenzstufen sich zu einem Hexachord zusammenfügen:

Das Prinzip, sechs Teiltonarten, deren Kadenzstufen ein Hexachord bilden, zu einer ›geschlossenen Sozietät‹ zusammenzufassen, vermittelt den Übergang von der Modalität zur Dur-Moll-Tonalität, weil die Teiltonarten sowohl Modi also auch Dur- oder Molltonarten sein können, ohne daß der Sinn des Systems gefährdet wäre. Ob die Teiltonart G in mixolydischer oder in Dur-Gestalt erscheint, ist gleichgültig, solange ihre Bedeutung in nichts anderem besteht, als die Sol-Stufe des Tonartensystems c-d-e-f-g-a = Ut-Re-Mi-Fa-Sol-La zu repräsentieren.[100]

Dieses hierarchisch geordnete System lässt sich in erster Instanz auf die Familie der sechs authentischen Modi beziehen, und zwar in der von Gioseffo Zarlino vorgenommenen Umsortierung der Glarean’schen Modi.[101] In zweiter Instanz beinhaltet es dann auch modale Modifikationen der einzelnen Teiltonarten. In Bezug auf die erste Instanz dieser Hierarchie ist die Rolle des Hexachords als unterliegende ordnende und in sich geschlossene Struktur durchaus adäquat, und Mengozzis Kritik auch an Zarlino als Hexachord-Theoretiker erscheint – aus mathematischer Sicht – als nicht gerechtfertigt.

4. Dahlhaus’ Revision der Funktionstheorie und die strukturellen Modi

Es wäre vermessen, anhand der bislang diskutierten Begriffe der Diatonizität zu Dahlhaus’ eigentlichem Untersuchungsthema – der Entstehung der harmonischen Tonalität – Stellung beziehen zu wollen. Für die Zwecke des hier vorliegenden Aufsatzes muss es genügen, einzelne Schlaglichter auf seine Argumentationen zu werfen, und zwar vor allem hinsichtlich der Integration von historischen und systematischen Gesichtspunkten. Im Zusammenhang mit seiner Interpretation der hexachordalen Ordnung der Teiltonarten als »einem Zwischenzustand der Indifferenz« im Übergang von der Modalität zur Dur-Moll-Tonalität erscheint immerhin ein Querverweis sinnvoll auf den Begriff der ›Pivot-Regionen‹ im Rahmen von Fred Lerdahls ›Tonal-Pitch-Space‹-Modell[102], welches hierarchische Tonhöhen-Strukturen in der harmonisch tonalen Musik im Einklang mit kognitiven Grundannahmen zu erfassen trachtet. Innerhalb des (Gottfried Weber zugeschriebenen) Raums der ›tonalen Regionen‹ (siehe Abbildung) isoliert Lerdahl hexachordale Teilbereiche, deren Elemente er ›Pivot-Regionen‹ nennt. Jede dieser Regionen repräsentiert eine diatonische Dur- oder Molltonart mit ihren sieben Stufen.

Abbildung 6: Der hexachordal strukturierte Raum der Regionen bei Fred Lerdahl (2001)

Lerdahl folgt damit ziemlich genau dem Bild einer hexachordal geordneten Sozietät von Teiltonarten, deren Stufen er noch Abstandsmaße unterlegt. Die ›modernere‹ Anordnung des Hexachords in Webers Raum der Regionen in Form zweier kurzer Quintenketten für die Dur- bzw. für die Moll-Regionen spiegelt die Tatsache wider, dass die Durstufen I, IV, V untereinander und die Mollstufen iv, ii, iii untereinander kurze Quintenketten innerhalb der Diatonik bilden, was wiederum eine Konsequenz der generischen Intervallstruktur (3, 3, 1) des Dreiklangs innerhalb der Quintenkette der Diatonik darstellt.[103]

Mit diesem Querverweis rücken nun jene Begriffe der Diatonizität in das Blickfeld, welche die harmonische Tonalität betreffen. Mit den abschließenden Bemerkungen geht es vordringlich darum, die bislang angestellten Überlegungen abzurunden, ohne die damit tangierten Inhalte ausführlich zu behandeln. Sie betreffen die theoretische Aufklärung des Verhältnisses zweier Diatonizitätsbegriffe, des Sieben-Stufen-Systems und des Drei-Dreiklangs-Systems, und der daran geknüpften Frage nach den Prinzipien der ›eigentlichen Harmoniebewegung oder Kadenzierung‹, wie Hugo Riemann sie nennt.

Während die Stufentheorie darauf abzielt, die Dreiklänge und Septakkorde unter dem Dach der Diatonik zu beschreiben, erkennt ihnen die Funktionstheorie eine gewisse Autonomie zu und deklassiert dagegen die Diatonik zu einer peripheren Hülle des Drei-Dreiklangs-Systems. Dahlhaus’ Reform der Funktionstheorie ist ein wichtiger Bestandteil seiner ›Theorie der harmonischen Tonalität‹, die ihrerseits eine unverzichtbare Voraussetzung für die Untersuchung ihrer Entstehung darstellt. Am Ende des ersten Kapitels der Untersuchungen macht er den Vorschlag zu einer Synthese aus Stufentheorie und Elementen der Funktionstheorie, die er beide einer kritischen Revision unterzieht.

Um zu sein, was ihr Name verspricht, müßte die Stufentheorie die Akkordstufen einer Tonart in ihrem Verhältnis zueinander und zur Tonika charakterisieren, statt sie bloß zu zählen; eine Serie von Ordnungszahlen ist keine Theorie, und die Funktionstheorie scheint zu ergänzen, was der Stufentheorie fehlt, eine eindeutige fest umrissene Charakteristik der Stufen.[104]

Als wichtige Erfüllungsbedingung für seine Reformation des Funktionsbegriffs nennt Dahlhaus die Auflösung des Problems der II. Stufe:

Die Selbständigkeit der II. Stufe wird von der Stufentheorie behauptet, von der Funktionstheorie geleugnet. Und der Unterschied läßt sich, wie eine Analyse des Funktionsbegriffs zeigen wird, nicht durch eine Korrektur der Stufentheorie, sondern nur durch eine Umformulierung der Funktionstheorie auflösen. Zugleich wird deutlich werden, daß der Funktionsbegriff von Riemanns Methode, die Nebenstufen zu dissonierenden Varianten der Hauptstufen zu degradieren, getrennt werden kann, so daß es möglich wird, am Stufenbegriff festzuhalten, ohne den Funktionsbegriff preiszugeben.[105]

Dahlhaus’ Lösung des Problems zielt auf eine Abgrenzung des Funktionsbegriffs vom Substanzbegriff eines Drei-Dreiklangs-Systems, auf welchen Riemann seine Erklärungsansätze der Funktionstheorie gründet. Dahlhaus genügt dagegen das Bestehen von Differenzen als einer minimalen substanziellen Basis, die er bei Stufen im Quintabstand und im Sekundabstand als gegeben ansieht.

Die Erfahrung, die der Funktionstheorie zugrunde liegt, läßt sich am einfachsten durch den Satz ausdrücken, daß Akkorde im Quint- oder Sekundabstand funktional different, und Akkorde im Terzabstand funktional indifferent sind.[106]

Weil unter vier diatonischen Dreiklängen mindestens zwei im Terzabstand sein müssen, folgert Dahlhaus, dass deswegen die Zahl der funktional differenten Akkorde auf drei beschränkt ist. Dieser strukturalistisch anmutende Ansatz scheint auf den ersten Blick auf eine ›arbiträre‹ Signifikation der Funktionen T, S, D durch Tripel paarweise funktional differenter diatonische Stufen hinauszulaufen. In Bezug auf die Beziehung der drei Funktionen untereinander scheint Dahlhaus indes an deren dialektischer Bestimmung festzuhalten:

Andererseits wäre an das dialektische Schema zu erinnern, das von Riemann 1872 als ›musikalische Logik‹ exponiert, später aber fallengelassen wurde, weil die ›musikalische Logik‹, die Funktionsbezeichnungen und das ›dualistische‹ System insofern unvereinbar sind, als jede Verbindung von zwei Momenten das dritte ausschließt. Statt des dialektischen Schemas aber kann der ›Dualismus‹ preisgegeben werden.[107]

Angesichts des dialektischen Dreischritts als eines allgemeinen – nicht musikspezifischen – Denkprozesses lenkt Dahlhaus – anders als Moritz Hauptmann[108] – sein Augenmerk also auf das Bestehen von Differenzen in der musikalischen Substanz, welche Tonalität als das Ergebnis einer dialektischen Sinngebung entstehen lassen. In Hinblick auf Dahlhaus’ eigenes Ringen um den Theoriebegriff ist man deshalb in der Versuchung, diesen konkreten Beitrag vor dem Hintergrund jener Erfüllungsbedingung zu betrachten, welche Dahlhaus später perspektivisch an die Musiktheorie heranträgt, nämlich die »Grundformen zu bestimmen, in denen der musikalisch sich verwirklichende Geist tätig ist«.[109] Dem steht allerdings jene zurückhaltende Stellungnahme vom Ende der Einleitung des Theoriekapitels der Untersuchungen entgegen, die zwar in ontologischer Hinsicht alle Möglichkeiten offenhält, aber als Gegenstand der Untersuchungen ausschließt (siehe Zitat gegen Ende von Abschnitt 1).[110]

Unterdessen ist daher auch die mathematische Musiktheorie am Zuge, sich in die Diskussion um die Konstitution von Tonalität einzubringen und dabei auch den Begriff des ›Toncharakters‹ auszuloten mit dem Ziel, eine an den dreiwertigen Funktionsbegriff bestangepasste musikalische Substanz zu identifizieren. Einen konkreten Anknüpfungspunkt hierzu bietet ein frappierendes Argument, mit dem Dahlhaus einem naheliegenden Einwand zu begegnen trachtet:

Man könnte einwenden, daß der Zusammenhang zwischen den Funktionen und den Stufenabständen nicht als Begründung der Funktionen durch die Differenzen und Indifferenzen der Abstände, sondern als zufällige Koinzidenz zu verstehen sei; daß zwei Momente zusammentreffen besage nicht, daß das eine die Bedingung des anderen sei. Doch zeigt eine Analyse der Quintschrittsequenz I-IV-VII-III-VI-II-V-I, daß es sich um eine Abhängigkeit handelt, denn die Quintschrittsequenz ist einerseits nicht ohne Rest funktional bestimmbar und erscheint andererseits als Ausnahme von der Regel der differenten und indifferenten Stufenabstände.[111]

Bemerkenswert ist an diesem Argument, dass Dahlhaus mit der Quintschrittsequenz den Inbegriff der Sechter’schen Stufentheorie zur Sprache bringt und die Schwierigkeit ihrer funktionsharmonischen Deutung ausgerechnet dazu verwendet, um die Plausibilität seiner reformierten Funktionstheorie zu stützen. Dreh- und Angelpunkt dieses Arguments ist der von Riemann[112] – teilweise unter Berufung auf Fétis – vorgebrachte Gedanke einer Suspendierung der ›eigentlichen Harmoniebewegung‹ in der Sequenz.[113] Weil jeder Versuch, alle sieben Stufen funktional zu deuten, notwendigerweise zu einer Verletzung der Regel von den differenten und indifferenten Stufen führt, scheint Dahlhaus gerade darin die Erklärung für den behaupteten Suspendierungseffekt zu sehen. Mit dieser These scheint er das ärgste Problem der Funktionstheorie in eine Tugend zu verwandeln. Anstatt jedoch diese These in die Form einer ontologisch verbindlichen kühnen Hypothese zur musikalischen Geistestätigkeit zu gießen, begnügt er sich in seinem Résumé mit einem fragwürdigen Bekenntnis epistemologischer Natur:

Eine Theorie aber, die gerade dort versagt, wo auch das Phänomen, das sie erklären soll, ins Vage und Unbestimmte gerät, darf als adäquat gelten.[114]

Die Quintschrittsequenz berührt jedenfalls einen zentralen Punkt in der Auseinandersetzung mit den tonalen Funktionen. Was in Dahlhaus’ Argument eigentlich keine Rolle spielt, ist die Bewegungsmetaphorik, welche traditionell auf die Quintordnung der Stufen projiziert wird. Die bloße Kombinatorik funktional differenter Stufen läuft einem Bewegungs- oder Fortschreitungsbegriff auf der Substanzebene zwar nicht zuwider, aber sie versagt ihm zumindest die Unterstützung und befördert eher die Idee einer Abfolge von Harmonieereignissen. Dagegen passt die Metapher der Harmoniebewegung sehr gut zur vollen Quintschrittsequenz, die einer klar definierten Bahn folgt, welche sogar mit Handschins Skala der diatonischen Toncharaktere übereinstimmt. Im Vertrauen insbesondere in die Vernunft des von Riemann gewählten Terminus wäre also erneut auch nach einem Konfigurationsraum für die ›eigentliche Harmoniebewegung‹ zu suchen, nach einem Drei-Stufen-System als musikalischer Substanz für eine ›motivierte Signifikation‹ der tonalen Funktionen.

Zur Debatte steht konkret die Theorie der strukturellen Modi[115], die Karst de Jong und der Autor im Rahmen der algebraischen Theorie der Modi formuliert haben. Der Begriff der ›strukturellen Skala‹ taucht bereits im ersten Absatz in Carey/Clampitts 1989 zu den wohlgeformten Skalen auf, und zwar mit explizitem Hinweis auf die Konstellation der Fundamente der Tonika-, Subdominant und Dominantdreiklänge:

A single structural principle accounts for pentatonic, diatonic and chromatic scales. The same structure, that of a ›well-formed scale‹ also underlies the tonic-subdominant-dominant relationship, the 17-tone Arabic and 53-tone Chinese theoretical systems, and other pitch collections in non-western music.[116]

Die wohlgeformten strukturellen 3-Ton-Skalen, wie z.B. C-F-G, gehören zum Begriffsumfang der Myhill-Eigenschaft und folglich finden alle bislang über diesen Begriff zusammengetragenen Fakten Anwendung auf diese Skala. Ihre beiden authentischen Modi ba|b bzw. ab|b haben bereits als Quart-Quint-Oktav-Gerüst bzw. Ganzton-Quint-Oktav-Gerüst im Zusammenhang mit der Konstruktion der authentischen diatonischen Modi durch Ausfüllung von Tetrachorden Erwähnung gefunden. Sie werden als erster bzw. zweiter ›struktureller Modus‹ bezeichnet. Dazu gibt es – ganz analog zur Situation der diatonischen Modi – einen dritten Modus, der eine ›amorphe‹ Oktavgattung aufweist, aber keine authentische Teilung.

Abbildung 7: Schrittintervall-Muster und Quint/Quart-Faltungen der drei strukturellen Modi

Die traditionelle fundierende Rolle des Drei-Dreiklangs-Systems für die Funktionstheorie wird hier zugunsten eines einfachen 3-Stufen-Systems ausgeblendet, wobei der Begriff der ›Stufe‹ nur für Akkordfundamente steht.[117] Die Beschreibungsebene der harmonischen Tonalität, in welcher die ›strukturellen Modi‹ zur Anwendung kommen, ist also der Fundamentalbass, welcher dadurch tonal interpretiert wird.

Das von Dahlhaus angesprochene Problem der II. Stufe erfährt eine plausible Auflösung, die sowohl dem Standpunkt der Stufentheorie als auch dem der Funktionstheorie gerecht wird. Wenn man die strukturellen Modi als in die Diatonik eingebettet betrachtet, dann korrespondiert der erste Modus mit der Fundamentfortschreitung I-IV-V-(I) und der zweite mit der Fundamentfortschreitung I-II-V-(I). Die zweite strukturelle Stufe, welche in allen strukturellen Modi die Subdominante signifiziert, entspricht also – je nach Modus – einmal der diatonischen Stufe IV und einmal der II.

Eine zweite Deutung erfährt die II. Stufe als ›strukturelle Alteration‹ der IV. Stufe. Der verallgemeinerte Alterationsbegriff leitet sich direkt aus der Myhill-Eigenschaft ab, denn für jedes generische Intervall (Prime und Oktave ausgenommen) weisen dessen zwei spezifische Varianten immer das gleiche Differenzintervall auf, die ›verallgemeinerte übermäßige Prime‹. Im vorliegenden Fall handelt sich dabei um die (diatonische) kleine Terz m3, die Differenz aus Quarte P4 und großer Sekunde M2. Das Intervall wird als ›strukturelle übermäßige Prime‹ bezeichnet und ist die Differenz der beiden strukturellen Schrittintervalle.[118]

Wie auch im Falle der Diatonik kann eine Alteration einen Moduswechsel bedeuten oder aber die chromatische Veränderung einer Stufe. So kann die strukturelle Alteration des Fundaments F zum Fundament D einerseits eine Modulation des ersten strukturellen C-Modus in den zweiten und andererseits aber auch die Alteration der zweiten Stufe innerhalb des ersten strukturellen C-Modus bedeuten. Ein typischer Fall für die letztere Möglichkeit ist die Fundamentfolge C-F-D-G-C, in der D aus Sicht der Stufentheorie z.B. als II oder V/V analysiert würde. Die strukturelle Annotation lautet dann C₁: T-S-#S-D-T. Im zweiten strukturellen Modus ist es dagegen die I. Stufe, welche der Alteration unterworfen ist: Die Fundamentfolge C-A-D-G-C hat dann die Annotation C₂: T-#T-S-D-T. Während die Analyse des Fundaments D als Stammton des zweiten Modus eine stärkere Affinität zur Auffassung der Stufentheorie besitzt, suggeriert die Analyse des Fundaments D als strukturelle Alteration des Fundaments F im ersten Modus eine stärkere Affinität zu Rameaus ›double emploi‹ und zu Riemanns Ableitung der Parallelklänge als Scheinkonsonanzen.

Am Rande sei angemerkt, dass die strukturellen Modi einen Sonderfall unter den wohlgeformten Modi bilden, als es hier keine algebraische Bevorzugung der Be-Richtung gibt. Es gibt nur eine Gattung der Quarte, und sie stimmt mit dem sekundären Schrittintervall überein. Wie die obigen Argumente suggerieren, kommt in der Anwendung der Kreuz-Richtung der Quint/Quartfaltungen sogar eine größere Bedeutung zu, was wiederum mit der Prominenz des Quintfalls im Fundamentalbass zu tun hat.[119]

Wie bereits im ersten Abschnitt angekündigt, soll in diesem Zusammenhang noch einmal auf Dahlhaus’ Auseinandersetzung mit der Frage nach einer natürlichen Begründung der Dur- bzw. Molltonalität auf der Grundlage des Toncharakters eingegangen werden. Mit einem ersten Argument stützt Dahlhaus zunächst Handschins Erklärungsansatz, wonach die Lage der Grundtöne der Stufen IV, I und V auf der Be-Seite der Quintenkette deren gesetzteren und affirmativeren Status begründen sollen:

Es scheint aber, als ändere die Differenz zwischen dem Quintensystem f-c-g-d-a-e-h und dem Quint-Terz-System f-a-c-e-g-h-d nichts an dem Sachverhalt, daß die Ähnlichkeit oder Unähnlichkeit der Toncharaktere von der Nähe oder Ferne der Töne in der Quintenreihe abhängt, denn auch in der C-dur-Tonart, die das Quint-Terz-System f-a-c-e-g-h-d voraussetzt, sind die Terztöne a und e in ihrem ›Charakter‹ einander ähnlicher als der Terzton dem Subdominantgrundton f. Das Quint-Terz-System der Tonbeziehungen und das Quintensystem der Toncharaktere schließen sich also nicht aus.[120]

Darauf stützt sich dann ein zweites kompromittierendes Argument, welches auf der Übertragung des ersten Arguments auf die Situation der Molltonart beruht:

Die Molltonalität jedoch verkehrt die Toncharaktere ins Gegenteil: die Behauptung, daß f und c auch als Mollterzen ›gesetzt und affirmativ‹ seien, wäre paradox. Zwar sind f und c in Moll, nicht anders als in Dur, einander ähnlicher als f und d oder c und a; die Ähnlichkeit, deren Maß der Quintabstand ist, bleibt bestehen, aber sie wechselt ihren Inhalt. Nur die formale Definition des Toncharakters als ›nach innen gewendete‹ Position im System ist demnach unwiderlegbar. Wird aber die inhaltliche preisgegeben, so ist zugleich die ›natürliche‹ Begründung der Dur-Tonalität aufgehoben.[121]

Dahlhaus’ Kritik beruht auf der Annahme, dass sowohl die Dreiklänge als auch deren Fundamente ihre Tonbedeutungen aus einer gemeinsamen Einbettung in ein diatonisches Quint-Terz-System beziehen. Demgegenüber zieht der Ansatz der strukturellen Modi eine Alternative in Betracht, der zufolge die Fundamente ungeachtet der auf ihnen errichteten Akkorde eine eigene Struktur konstituieren, welcher dann die Unterscheidung von Dur- und Mollstufen auf einer weiteren Beschreibungsebene nachgeordnet ist. Dahlhaus’ Quint-Terz-System ist zu flach, um solch eine Differenzierung zu repräsentieren.

Den Abschluss dieses Plädoyers für eine neue alte Musiktheorie bietet deshalb ein verfeinerter Integrationsansatz, in welchem die Interaktion von Diatonik, Dreiklängen und Fundamenten auf eine gemeinsame Grundlage gestellt wird, die dem Begriff der Agmon-Diatonik entspricht. Überraschenderweise ist dieser neue Begriff logisch äquivalent zu einer neuen Ausdeutung des alten Begriffs der ›Subdominante‹.

Der Terminus ›soudominante‹ wird von Jean-Philippe Rameau in seiner Abhandlung Nouveau systême de musique théorique[122] im Sinne einer Unterdominante definiert, also als ein Ton, der eine Quinte unterhalb der Tonika zu finden ist. In der Abhandlung Génération harmonique[123] erweitert Rameau diese Definition um den Hinweis, dass dieser Ton (nach Versetzung in die Quarte über der Tonika) in der diatonischen Schrittordnung direkt eine Stufe unterhalb der Dominante zu finden ist.[124]

SOUDOMINANTE. C’est la quinte au-dessous, et par Renversement la Quarte du Son principal, dit Note-Tonique, et qui se trouve immédiatement au-dessous de la Dominante dans l’ordre Diatonique.[125]

Anlass zu dieser Erweiterung mag jene konkurrierende Motivation desselben Terminus gegeben haben, der zufolge es um den ›Ton unterhalb der Dominante‹ geht. Die Bezeichnungen für andere Stufen, wie ›sudominante‹ und ›sutonique‹ in Rameaus Thesaurus folgen ebenfalls dieser Motivation, welche zudem schon verbreitet gewesen ist.[126] Die konkurrierenden Motivationen haben nicht nur zu weiteren terminologischen Verwirrungen geführt[127], sondern dokumentieren auch divergierende musiktheoretische Schwerpunktsetzungen hinsichtlich der Konzeptualisierung von harmonischer Tonalität.

Neben dem Bezeichneten des Terminus ›Subdominante‹, der vierten Stufe der diatonischen Tonleiter, konkurrieren zwei Weisen musikalischen Gegebenseins, die man mit Gottlieb Frege dem ›Sinn‹[128] dieses Terminus zuschlagen sollte. Sie spezifizieren Tonbeziehungen durch Quinten bzw. durch Schritte und entsprechen den beiden im Begriff der wohlgeformten Skala miteinander verbundenen Koordinatensystemen. Deshalb ist es aus Sicht der formalen Begriffsanalyse interessant, Rameaus Definition als eine Gleichung zu lesen, die dann als Definition für einen bestimmten Skalenbegriff fungiert. Dass die Quarte über der Tonika und die Sekunde unter der Dominante zu ein und demselben Ton führen, klingt aufgrund der Intervallbezeichnungen wie eine Selbstverständlichkeit. Für eine allgemeine wohlgeformte Skala bedeutet diese Gleichheit jedoch, dass die Differenz aus dem Generatorintervall und dessen Oktavkomplement ein Schrittintervall der Skala sein muss. Für die chromatische Zwölfton-Skala ist dies beispielsweise nicht der Fall.[129]

Theoretisch müsste man damit rechnen, dass die Lösungen der ›Rameau-Gleichung‹ – man kann sie ›diazeuktische Skalen‹ nennen – einen neuen Knoten im Verband der formalen Diatonizitätsbegriffe definieren. Tatsächlich fallen sie aber mit der Extension jenes bereits ermittelten Knotens zusammen, der die Bezeichnung ›Agmon-Diatonik‹ trägt. Für wohlgeformte Skalen sind also die Eigenschaften der Kohärenz und Effizienz logisch äquivalent dazu, dass die Diazeuxis ein Schrittintervall ist.[130] Bei genauer Überlegung leuchtet dies ein, denn die Teilung der Diazeuxis zieht zwangsläufig das Bestehen mehrerer Ambiguitäten nach sich, während Agmon mit seinem Begriff nur eine einzige Ambiguität zulässt.

Die diazeuktischen Skalen zerfallen in transformationeller Hinsicht in einen ›disjunkten‹ und einen ›konjunkten‹ Typus je nach Auftreten der Sturm’schen Morphismen D/D^~ oder G/G^~ im ersten Transformationsschritt der Erzeugung von Modi dieser Skalen.[131] Die strukturellen Modi D(a|b) = ba|b und D^~(a|b) = ab|b exemplifizieren die kleinsten diazeuktischen Modi des disjunkten Typs und lösen damit – wie oben gezeigt – das Problem der II. Stufe auf elegante Weise. Analog bilden die generische Dreiklangs-Grundstellung G(a|b) = a|ab und der generische Sextakkord G^~(a|b) = a|ba die einfachsten Instanzen des konjunkten Typs.[132] Dies eröffnet die Perspektive, eine Theorie der harmonischen Tonalität zu entwickeln, deren Elemente als Lösungen von Rameaus Gleichung sämtlich unter den Begriff des diazeuktischen Modus fallen und die das von Dahlhaus favorisierte Quint-Terz-System in einer Weise verfeinern, die dessen Kritik an Handschins Leitidee hinter dem Toncharakter vorerst ins Leere laufen lassen. Damit wäre auch der Weg geebnet für die Inangriffnahme einer transdisziplinären Aufarbeitung jener Leitidee.